Demonstração das fórmulas das coordenadas do vértice

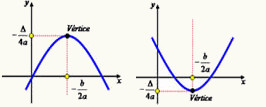
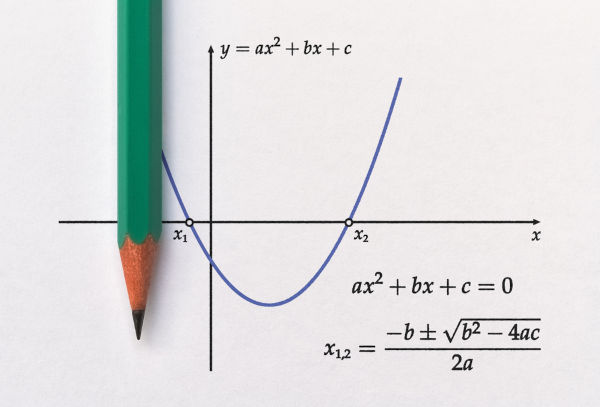
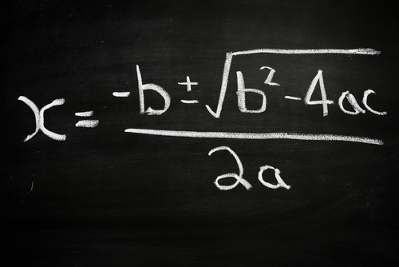Toda função do segundo grau pode ser representada geometricamente por uma parábola. Nesse caso, essas parábolas terão concavidade voltada para cima e, portanto, um ponto de mínimo, ou terão concavidade voltada para baixo e, por isso, um ponto de máximo. É o ponto de máximo (ou de mínimo) que é conhecido como vértice da parábola.

Supondo que o vértice de uma parábola seja V(x_v, y_v), então as coordenadas desse ponto podem ser obtidas pelas seguintes fórmulas:

x_v = – b
       2a

y_v = – Δ
       4a

A demonstração dessas duas fórmulas depende de uma outra técnica, que também pode ser usada para determinar as coordenadas do vértice, baseada na análise geométrica da parábola.

Tópicos deste artigo

• 1 - Como encontrar as coordenadas do vértice
• 2 - Demonstração das fórmulas

Como encontrar as coordenadas do vértice

Dada uma função do segundo grau, sabemos que seu gráfico é uma parábola. A figura a seguir é uma parábola qualquer que representa uma função f(x) = ax² + bx + c. As seguintes propriedades e características descritas são válidas para qualquer parábola.

As raízes da parábola são os pontos de encontro entre ela e o eixo x do plano cartesiano, portanto, podemos dizer que suas coordenadas são (x₁, 0) e (x₂, 0). Com relação a esse eixo, observe que o ponto x_v fica exatamente no ponto médio entre as raízes. Portanto, é possível determinar a coordenada x_v do vértice por meio da média entre as coordenadas x das raízes da parábola. Logo, x_v será:

x_v = x₁ + x₂
       2

Também podemos determinar y_v descobrindo a imagem da função f(x) = ax² +bx + c no ponto x_v. Para isso, devemos observar que a coordenada y ligada a x_v, na imagem anterior, é justamente y_v. Assim:

f(y_v) = a(y_v )² + by_v + c

Demonstração das fórmulas

A fórmula usada para determinar os valores de x₁ e x₂ é a de Bháskara. Pela fórmula de Bháskara, podemos afirmar que:

x₁ = – b + √Δ
       2a

x₂ = – b – √Δ
       2a

Substituindo esses valores na expressão:

x_v = x₁ + x₂
       2

Teremos:

Dessa forma, demonstrou-se a expressão usada para determinar a coordenada x do vértice de uma parábola em função dos coeficientes da função do segundo grau que essa figura representa. Para determinar a coordenada y do vértice, resolveremos a equação:

f(y_v) = a(y_v )² + by_v + c

Observe:

Fazendo a adição de frações, com base no mínimo múltiplo comum, temos:

Dessa maneira, demostramos a fórmula usada para calcular y do vértice com base nos coeficientes da função do segundo grau.