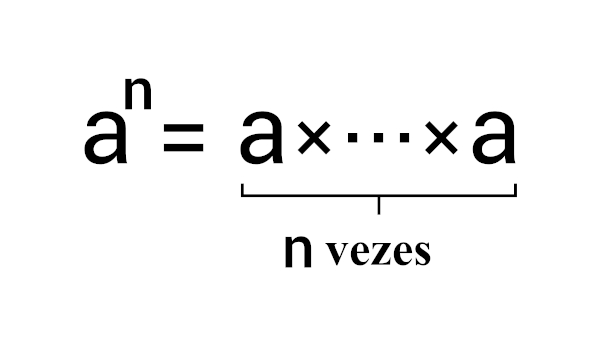A matemática é viva, intensa, impressionante e nos faz pensar, refletir e nos divertir. Conhecer a face divertida da matemática, com suas curiosidades e revelações, é fundamental para despertar o gosto por essa ciência fascinante que geralmente é vista com maus olhos. Vejamos algumas curiosidades que envolvem os números e quanta coisa interessante deixamos de aprender por achar que diversão e matemática não se misturam.
1. Raízes de números quadrados perfeitos
Observe os seguintes pares de quadrados perfeitos:
144 e 441 (Note o que esses números apresentam em comum)
Extraindo a raiz quadrada de cada um deles, obtemos:
![]()
O que você consegue perceber?
Veja mais dois pares de quadrados perfeitos:
169 e 961
Extraindo as raízes de cada um, teremos:
![]()
Conseguiu observar o que ocorre?
Veja que 144 e 441, 169 e 961 são pares de quadrados perfeitos compostos pelos mesmos algarismos só que escritos de trás para frente. O interessante é que suas respectivas raízes também apresentam essa característica.
Observe mais um exemplo:
Os pares de quadrados perfeitos 14884 e 48841 apresentam os mesmos algarismos só que escritos de trás para frente.
Calculando a raiz quadrada de cada um, temos:
![]()
Suas raízes também apresentam os mesmos algarismos só que escritos em ordem inversa.
2. O número mágico 1089
Vejamos o motivo de esse número ser chamado de número mágico.
Escreva um número de três algarismos distintos (diferentes).
598, por exemplo.
Escreva este número de trás para frente e subtraia o menor do maior.
895 – 598 = 297
Agora, inverta também esse resultado e efetue a adição.
792 + 297 = 1089
Independente do número escolhido, teremos sempre como resultado final o número 1089. Mas lembre-se, só vale para números de três algarismos distintos. Se utilizarmos, por exemplo, 555 ou 988 a propriedade não será válida.
3. A forma pitagórica de calcular potências
Pitágoras foi um grande matemático que se dedicou ao estudo geométrico, trigonométrico e dos números. Dentre seus inúmeros estudos ele descobriu outra forma de se calcular potências com expoente 2. Depois de muito estudo e observação, notou que qualquer potência de números naturais do tipo n2 pode ser obtida somando os n primeiros números naturais ímpares. Veja como funciona:
a) 62 = 1 + 3 + 5 + 7 + 9 + 11 = 36
b) 72 = 1 + 3 + 5 + 7 + 9 + 11 + 13 = 49
c) 42 = 1 + 3 + 5 + 7 = 16
d) 52 = 1 + 3 + 5 + 7 + 9 = 25