Coordenadas do vértice da parábola

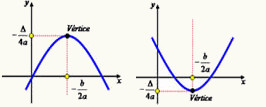
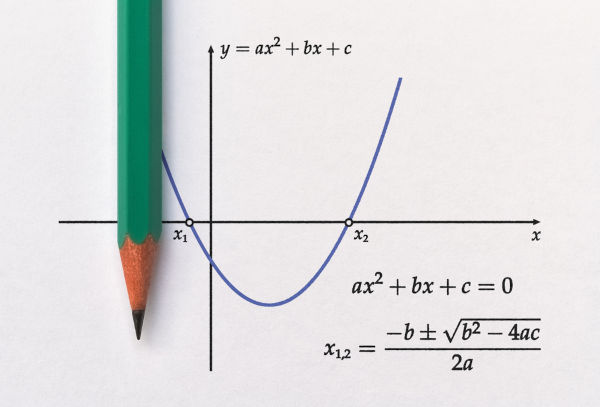
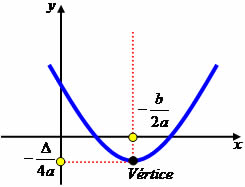
Toda função do 2º grau é do tipo f(x) = ax² + bx + c, com a ≠ 0. O gráfico de uma função do segundo grau é uma parábola que, dependendo do valor do coeficiente a, terá a concavidade voltada para cima ou para baixo. Se o coeficiente a for negativo ( a < 0 ) a concavidade da parábola será voltada para baixo. Se ocorrer o contrário, ou seja, a for positivo ( a > 0 ), a parábola terá a concavidade voltada para cima. A parábola apresenta alguns pontos notáveis: as raízes, que são os pontos onde o gráfico intercepta o eixo das abscissas, e o vértice, que pode ser o ponto de máximo absoluto ou de mínimo absoluto da função. Faremos o estudo do vértice da parábola, a fim de determinar as suas coordenadas e compreender sua importância no estudo da função do 2º grau.

Como foi dito anteriormente, o vértice da parábola pode ser o ponto de máximo absoluto ou de mínimo absoluto da função do 2º grau. Se a concavidade da parábola for voltada para cima, o vértice é o ponto de mínimo da função, ou seja, é o menor valor que a função pode assumir. Se a concavidade da parábola estiver voltada para baixo, o vértice é o ponto de máximo da função, ou seja, o maior valor que a função pode assumir. O uso desses conceitos é bastante útil na teoria de lançamentos oblíquos.

 Dada uma função do 2º grau f(x) = ax² + bx + c, as coordenadas do vértice V da parábola descrita por essa função são:

 Onde
? = b² - 4ac

Vejamos alguns exemplos de aplicação.

Exemplo 1. Verifique se as seguintes funções apresentam ponto de máximo ou mínimo absoluto.

a) f(x) = – 2x² + 3x + 5

Solução: No caso da função do 2º grau, para determinarmos se há ponto de máximo e mínimo absoluto basta verificar se a concavidade da parábola descrita pela função apresenta concavidade voltada para baixo ou para cima. Nesse caso, temos que:

a = – 2 < 0 → concavidade da parábola está voltada para baixo.

Como a concavidade da parábola está voltada para baixo, a função apresenta ponto de máximo absoluto, que é o vértice da parábola.

b) y = 5x² – 3x

Solução: Temos que

a = 5 > 0 → concavidade da parábola está voltada para cima.

Assim, podemos afirmar que a função apresenta ponto de mínimo absoluto, que é o vértice da parábola.

Exemplo 2. Determine as coordenadas do vértice da parábola descrita pela função f(x) = 2x² – 4x + 6.

Solução: Analisando a função f(x) = 2x² – 4x + 6, obtemos:

a = 2, b = – 4 e c = 6

Segue que:

Exemplo 3. Uma bala é atirada de um canhão e descreve uma parábola de equação y = -9x² + 90x. Determine a altura máxima atingida pela bala do canhão, sabendo que y é a altura em metros e x é o alcance, também em metros.

Solução: Como a parábola possui equação y = – 9x² + 90x, podemos constatar que sua concavidade está voltada para baixo e que a altura máxima atingida pela bala de canhão corresponde à coordenada y do vértice, uma vez que o vértice é ponto de máximo absoluto.

Assim, para determinar a altura máxima atingida pela bala do canhão, basta determinar o valor y do vértice.
Temos que: a = – 9, b = 90 e c = 0. Logo, teremos:

Portanto, a altura máxima atingida pela bala de canhão é de 225 metros.