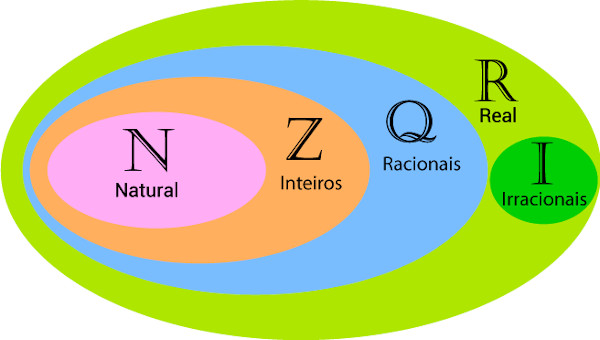
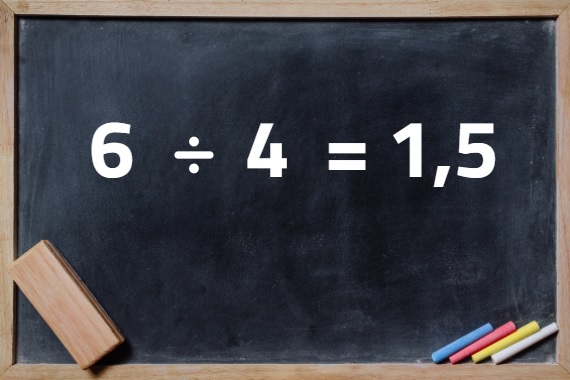Quais são os conjuntos numéricos?

Os conjuntos numéricos surgiram, no decorrer da história, com as necessidades do ser humano. Tem-se atualmente os seguintes conjuntos: conjunto dos números naturais ( \(\mathbb{N}\) N ); conjunto dos números inteiros ( \(\mathbb{Z}\) ); conjunto dos números racionais ( \(\mathbb{Q}\) ); conjunto dos números irracionais ( \(\mathbb{I}\) ); conjunto dos números reais ( \(\mathbb{R}\) ); conjunto dos números complexos ( \(\mathbb{C}\) ).

Conjuntos numéricos: quais são eles?

Os conjuntos numéricos surgiram, no decorrer da história, com as necessidades do ser humano. Tem-se atualmente os seguintes conjuntos:

conjunto dos números naturais (\(\mathbb{N}\) );
conjunto dos números inteiros (\(\mathbb{Z}\));
conjunto dos números racionais (\(\mathbb{Q}\));
conjunto dos números irracionais (\(\mathbb{I}\));
conjunto dos números reais (\(\mathbb{R}\));
conjunto dos números complexos (\(\mathbb{C}\)).

Tópicos deste artigo

Resumo sobre conjuntos numéricos

O conjunto dos números naturais, representado por \(\mathbb{N}\), é composto pelos números {0, 1, 2, 3, 4, 5...}, indo até o infinito.
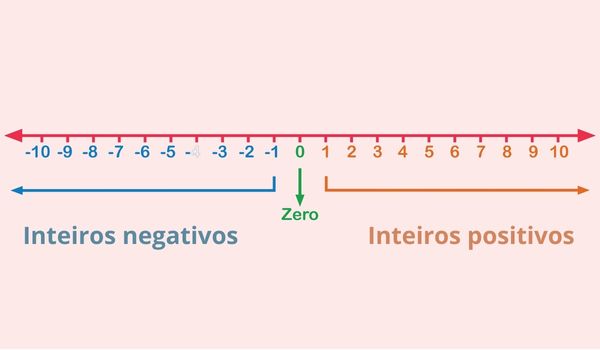
O conjunto dos números inteiros, representado por \(\mathbb{Z}\), é uma ampliação do conjunto dos números naturais, sendo composto pelos números naturais e os números negativos opostos a eles {... -3, -2, -1, 0, 1, 2, 3...}.
O conjunto dos números racionais, representado por \(\mathbb{Q}\), é a ampliação do conjunto dos números inteiros e é composto pelos números que podem ser representados como uma fração.
O conjunto dos números irracionais, representado por \(\mathbb{I}\), é o contrário dos números racionais, pois é composto por todos os números que não podem ser escritos na forma de uma fração.
O conjunto dos números reais, representado por \(\mathbb{R}\), é composto pela união dos números irracionais e os números racionais.

O conjunto dos números complexos, representado por \(\mathbb{C}\), é ampliação do conjunto dos números reais. Ele é composto por todos os números reais e a raiz quadrada de números negativos; são números escritos da forma a + bi.
Existem três operações com conjuntos: a união, a intersecção e a diferença.
Ao estudar o conjunto dos números reais, podemos formar subconjuntos dos números que estão entre a e b. Esses conjuntos são conhecidos como intervalos numéricos.

Videoaula sobre conjuntos numéricos

Conjunto dos números naturais

O conjunto dos números naturais foi o primeiro conjunto numérico que surgiu devido à necessidade humana de quantificar e contabilizar objetos do dia a dia. Ele é formado pelos números {0, 1, 2, 3, 4, 5...} e representado pela letra \(\mathbb{N}\). Inicia-se no zero e vai até infinito.

→ Subconjuntos dos números naturais

\(\mathbb{N}\ast\ ={1,\ 2,\ 3,\ 4,\ 5...}\) — conjunto dos números naturais não nulos, ou seja, é o conjunto dos números naturais sem o zero.
\(\mathbb{N}_p={0,\ 2,\ 4,\ 6,\ 8...}\) — conjunto dos números naturais pares.
\(\mathbb{N}_i={1,\ 3,\ 5,\ 7,\ 9...}\) — conjunto dos números naturais ímpares.
\(\mathbb{N}_5={0,\ 5,\ 10,\ 15,\ 20\ ...}\) — conjunto dos números naturais múltiplos de 5.

Não pare agora... Tem mais depois da publicidade ;)

Conjunto dos números inteiros

O conjunto dos números inteiros é formado pelos números naturais e os números negativos opostos a eles, ou seja, {... -3, -2, -1, 0, 1, 2, 3...}, e surgiu devido à necessidade de se representar números abaixo de zero, como para a medição de temperatura ou para as relações comerciais.

O conjunto dos números inteiros \(\mathbb{Z}\) é uma ampliação do conjunto dos números naturais, ou seja, todos os naturais são inteiros. Além dos naturais, nesse conjunto, há também os números opostos a eles.

→ Subconjuntos dos números inteiros

\(\mathbb{Z}\)* = {... -4, -3, -2, -1, 1, 2, 3, 4...} — conjunto dos números inteiros não nulos, ou seja, é o conjunto dos números inteiros sem o zero.
\(\mathbb{Z}\)₊ = {0, 1, 2, 3, 4, 5...} — conjunto dos números inteiros e não negativos.
\(\mathbb{Z}\) _– = {... -5, -4, -3, -2, -1, 0} — conjunto dos números inteiros não positivos.
\(\mathbb{Z}\)^*₊= {1, 2, 3, 4, 5...} — conjunto dos números inteiros positivos e sem o zero.
\(\mathbb{Z}\)^*_–= {... -5, -4, -3, -2, -1} — conjunto dos números inteiros negativos e sem o zero.

Conjunto dos números racionais

O conjunto dos números racionais é formado por todos os números que podem ser escritos como uma fração e é representado pela letra \(\mathbb{Q}\). Ele é uma ampliação do conjunto dos inteiros, ou seja, todo número inteiro é um número racional, pois os números inteiros podem ser representados como uma fração.

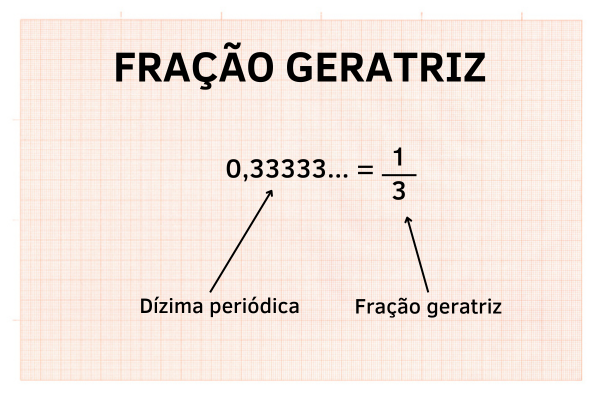
Além dos números inteiros, temos os números fracionários, que podem ser representados como frações ou números decimais, por exemplo: \(\frac{1}{2}\), \(\frac{12}{5}\), \( \frac{8}{9}\). Os números decimais e as dízimas periódicas pertencem a esse conjunto, pois podem ser representados como fração, como 2,5; 1,333...

De modo geral, temos que:

\(\mathbb{Q}={\frac{a}{b}|\ a\ \epsilon\ \mathbb{Z}\ e\ b\ \epsilon\ \mathbb{Z}^\ast}\ \)

O conjunto dos números racionais é igual a uma fração a sobre b, em que a pertence ao conjunto dos números inteiros e b pertence ao conjunto dos números inteiros não nulos.

→ Subconjuntos dos números racionais

\(\mathbb{Q}\)* = conjunto dos números racionais não nulos.
\(\mathbb{Q}\)₊ = conjunto dos números racionais não negativos.
\(\mathbb{Q}\)_– = subconjunto dos números racionais não positivos.
\(\mathbb{Q}\) *₊ = subconjunto dos números racionais positivos.
\(\mathbb{Q}\) *_–= subconjunto dos números racionais negativos.

Importante: Em relação aos subconjuntos que podem ser formados com o conjunto dos números racionais, é necessário ressaltar a densidade dos números irracionais, pois, entre dois números racionais, existem infinitos números racionais e irracionais, por exemplo, entre o 0 e o 1, há 0,5; 0,25; 0,02; 0,00000001 etc.

Conjunto dos números irracionais

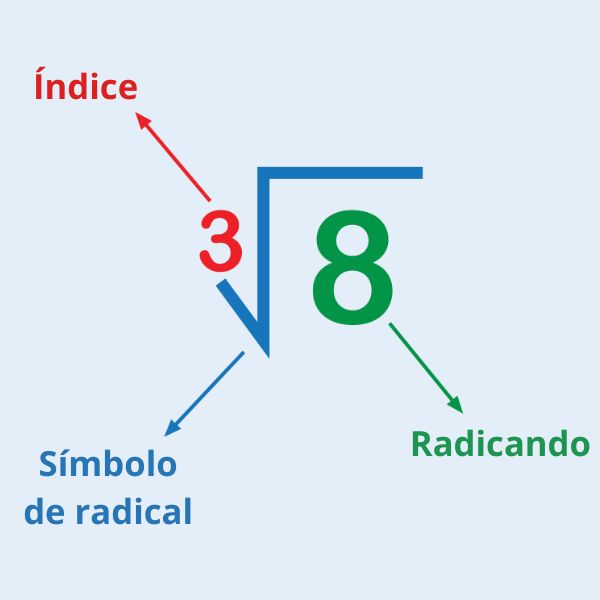
O conjunto dos números irracionais é o oposto do conjunto dos números racionais, então, ele é formado pelos números que não podem ser representados como uma fração, que, nesse caso, são as dízimas não periódicas. Vale ressaltar que uma raiz não exata tem como resposta uma dízima não periódica, logo, \(\sqrt2\), por exemplo, é um número irracional. O conjunto dos números irracionais pode ser representado por ð•€.

Cabe destacar que o conjunto dos números irracionais causou inquietação nos matemáticos, já que, diferentemente dos anteriores, ele não é uma ampliação de conjunto, mas sim um conjunto de números que não satisfazem a definição de números racionais. Para representar os números conhecidos até então por um único conjunto, surgiu um novo conjunto numérico, posterior ao dos números irracionais: o conjunto dos números reais.

Veja também: Raiz quadrada aproximada — como calcular uma raiz quadrada não exata?

Conjunto dos números reais

O conjunto dos números reais nada mais é que a união entre o conjunto dos racionais e o conjunto dos irracionais. Sabendo que o conjunto dos números racionais contém também o conjunto dos números inteiros e o conjunto dos números naturais, então todo número natural, inteiro, racional ou irracional é também um número real. O conjunto dos números reais é representado por \(\mathbb{R}\). Então temos que \(\mathbb{R}=\mathbb{Q}\cup\ \) ð•€ .

→ Subconjuntos dos números reais

\(\mathbb{R}\)* = conjunto dos números reais não nulos.
\(\mathbb{R}\)₊ = conjunto dos números reais não negativos.
\(\mathbb{R}\)_– = conjunto dos números reais não positivos.
\(\mathbb{R}\) *₊ = conjunto dos números reais positivos.
\(\mathbb{R}\)*_– = conjunto dos números reais negativos.

Atualmente, utilizamos o conjunto dos números reais para a maioria das situações do cotidiano. As medições, os cálculos e os estudos envolvendo função implicam, na maioria situações, os números reais. O conjunto dos números reais é o mais utilizado no cotidiano, ainda que exista uma ampliação para ele, o conjunto dos números complexos.

Conjunto dos números complexos

O conjunto dos números complexos é representado pela letra \(\mathbb{C}\). Nesse conjunto, representamos \(\sqrt{-1}\) por i, e os complexos correspondem aos números escritos da forma a + bi. O conjunto dos números complexos é uma ampliação do conjunto dos reais, logo, todo número real é um número complexo. Além dos números reais, estão presentes nesse conjunto as raízes de números negativos, que são números complexos, por exemplo:

\( 2+3i\)
\( 1+2i\)
\( -\ 4i\)

→ Subconjuntos dos números complexos

\(\mathbb{C}\)* = conjunto dos números complexos não nulos.
\(\mathbb{C}\)₊ = conjunto dos números complexos não negativos.
\(\mathbb{C}\)_– = subconjunto dos números complexos não positivos.
\(\mathbb{C}\)*₊ = subconjunto dos números complexos positivos.
\(\mathbb{C}\)*_–= subconjunto dos números complexos negativos.

Propriedades dos conjuntos numéricos

O conjunto dos números naturais está contido no conjunto dos números inteiros: \(\mathbb{N}\subset\mathbb{Z}\).
O conjunto dos números inteiros está contido no conjunto dos números racionais: \(\mathbb{Z}\subset\mathbb{Q}\).
O conjunto dos números racionais está contido no conjunto dos números reais: \(\mathbb{Q}\subset\mathbb{R}.\).
O conjunto dos números reais está contido no conjunto dos números complexos: \(\mathbb{R}\subset\mathbb{C}\).

Com base nisso, temos a seguinte relação de inclusão:

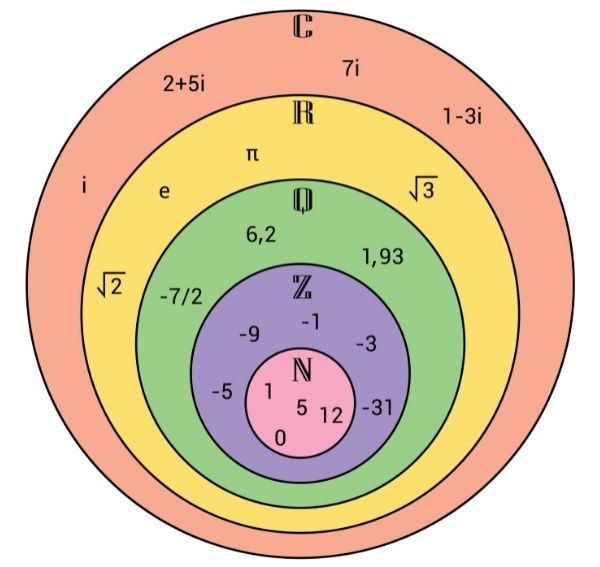
\(\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}\)

Além disso, o conjunto dos números irracionais está contido no conjunto dos números reais, mas ele não contém nenhum dos outros conjuntos. Como sabemos, os números reais estão contidos no conjunto dos números complexos, então temos que:

\(\mathbb{I}\subset\mathbb{R}\subset\mathbb{C}\)

Então podemos afirmar que o conjunto dos números complexos contém todos os demais conjuntos.

Representação dos conjuntos no diagrama

Podemos representar a relação de inclusão entre os conjuntos numéricos por meio de um diagrama.

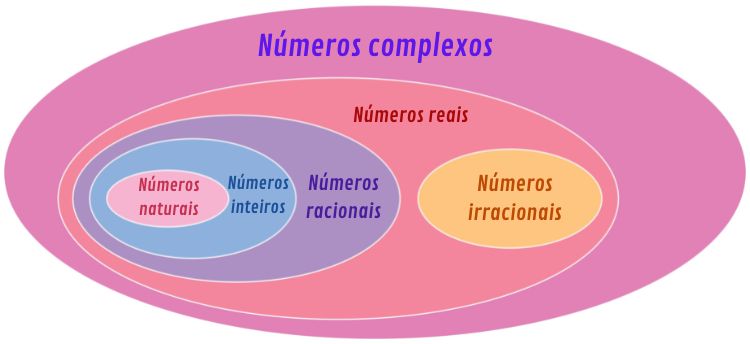
RepresentaÃ§Ã£o dos conjuntos numÃ©ricos no diagrama. — Representação dos conjuntos numéricos no diagrama.

Saiba mais: Diagrama de Venn — o método utilizado para representar conjuntos numéricos de forma geométrica

Operações com conjuntos

Na teoria dos conjuntos, podemos formar conjuntos que são subconjuntos dos conjuntos numéricos. São conhecidas três operações básicas dos conjuntos: a união, a intersecção e a diferença entre conjuntos.

União de conjuntos

RepresentaÃ§Ã£o da uniÃ£o de conjuntos. — Representação da união de conjuntos.

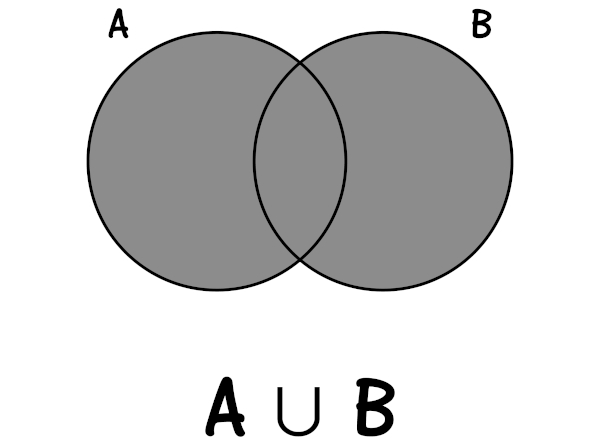
A união de conjuntos é a junção de todos os elementos de cada conjunto. Utilizamos o símbolo \(\cup\) entre os conjuntos para representar a união deles, por exemplo, \(A\cup B\) (lê-se: A união com B).

Exemplo:

Dado os conjuntos A = {1, 3, 5, 7} e B = {0, 2, 4, 6, 8}, a união entre eles é o conjunto:

\(A\cup B\) = {0, 1, 2, 3, 4, 5, 6, 7, 8}

Intersecção de conjuntos

RepresentaÃ§Ã£o da intersecÃ§Ã£o de conjuntos. — Representação da intersecção de conjuntos.

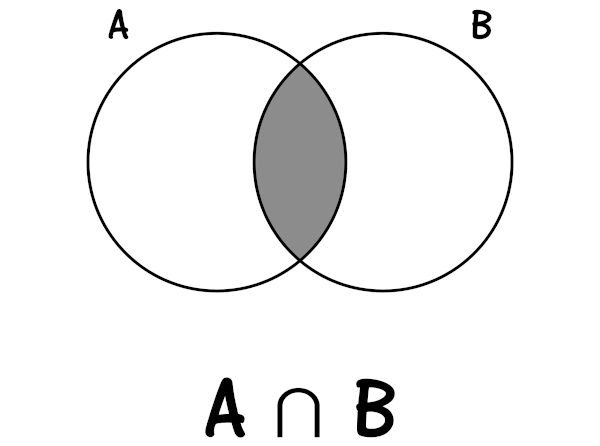
A intersecção de conjuntos é representada pelo símbolo \(\cap\). Ela é formada pelos elementos que pertencem simultaneamente a ambos os conjuntos. Dados os conjuntos A e B, sua intersecção é representada por \(A\cap B\).

Exemplo:

Tendo em vista os conjuntos A = {1, 2, 3, 4, 5} e B = {0, 3, 5, 7}, a intersecção entre eles, ou seja, \(A\cap B\) é:

\(A\cap B={3,\ 7}\)

Diferença de conjuntos

RepresentaÃ§Ã£o da diferenÃ§a de conjuntos. — Representação da diferença de conjuntos.

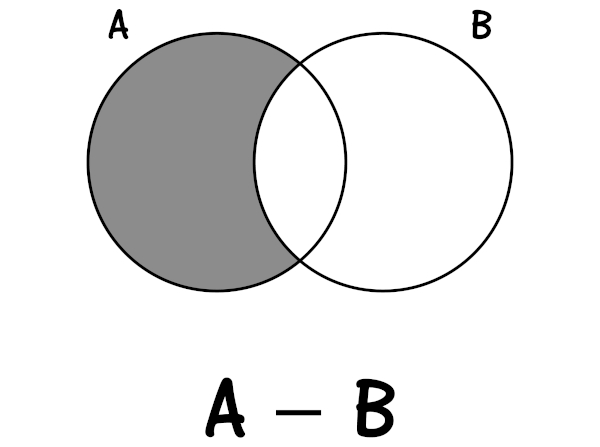
A diferença entre o conjunto A e B é a operação representada por A – B. Calcular essa diferença é retirar do conjunto A todos os elementos que pertencem ao conjunto B, encontrando assim os elementos que pertencem somente ao conjunto A.

Exemplo:

Considerando A = {1, 2, 3, 4, 5} e B = {0, 3, 5, 7}, calcularemos a operação A – B.

Sabemos que {3, 7} são elementos do conjunto A, que também pertence ao conjunto B, então eles não pertencem ao conjunto B – A, sendo assim, a diferença entre os conjuntos B e A será o conjunto:

A – B = {0, 1, 2, 4,}

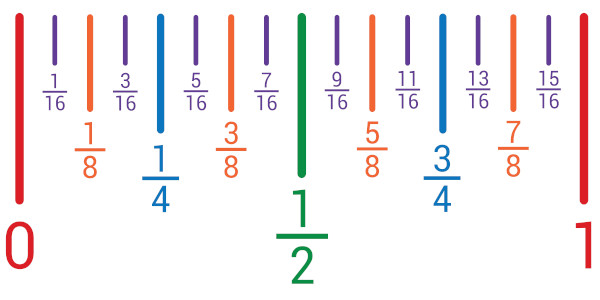
Intervalos numéricos

Ao estudar o conjunto dos números reais, podemos formar subconjuntos dos números que estão entre os números reais a e b. Esses conjuntos são conhecidos como intervalos numéricos.

Podemos ter um intervalo aberto, o que significa que ele é formado pelos números que estão entre a e b, sem incluir os extremos, ou seja, a e b.

RepresentaÃ§Ã£o de um intervalo aberto.

\(x\in\mathbb{R}|\ a<x<b\)

Nesse intervalo estão compreendidos todos os números entre a e b, sem incluir os próprios a e b.

Podemos ter um intervalo semiaberto, que possui um dos extremos incluídos no conjunto e o outro não. Podemos ter um semiaberto à direita ou um semiaberto à esquerda.

RepresentaÃ§Ã£o de um intervalo semiaberto.

\(x\ \in\ \mathbb{R}|\ a<x\le\ b\)

Segunda representaÃ§Ã£o de um intervalo semiaberto.

\(x\in\mathbb{R}|\ a\le x<\ b\)

Podemos ter intervalos fechados, quando os dois extremos estão inclusos no conjunto.

RepresentaÃ§Ã£o de um intervalo fechado.

\(x\ \in\ \mathbb{R}|\ a\le x\le\ b\)

Exercícios resolvidos sobre conjuntos numéricos

Questão 1

Sobre os conjuntos numéricos, julgue as afirmativas a seguir:

I. Todo número real é também um número racional.

II. Todo número real é também um número complexo.

III. O número \(-\frac{1}{2}\) é um número inteiro.

Marque a alternativa correta:

A) Somente a afirmativa I é verdadeira.

B) Somente a afirmativa II é verdadeira.

C) Somente a afirmativa III é verdadeira.

D) Todas as afirmativas são verdadeiras.

E) Todas as afirmativas são falsas.

Resolução:

Alternativa B

I. Todo número real é também um número racional. (Falsa)

O número real pode ser racional, mas também pode ser um irracional, logo, nem todo número real é racional.

II. Todo número real é também um número complexo. (Verdadeira)

O conjunto dos números reais está contido no conjunto dos números complexos, logo, todo número real é um número complexo.

III. O número \(-\frac{1}{2} \) é um número inteiro. (Falsa)

O conjunto dos números inteiros não é composto por frações, logo, a fração \(-\frac{1}{2} \) não é um número inteiro, mas sim um número racional.

Questão 2

Leia as frases abaixo sobre os conjuntos numéricos:

I. No conjunto {-2, -1, 0, 1, 2}, temos somente números naturais.

II. O número \(2\frac{3}{4} \) é um número racional.

III. O número \(\sqrt{-2}\) é um número complexo.

Marque a alternativa correta:

A) Somente a I é falsa.

B) Somente a II é falsa.

C) Somente a III é falsa.

D) Todas são verdadeiras.

Resolução:

Alternativa A

I. No conjunto {-2, -1, 0, 1, 2}, temos somente números naturais. (Falsa)

No conjunto, há números inteiros, pois -2 e -1 não são números naturais por serem negativos.

II. O número \(2\frac{3}{4}\) é um número racional. (Verdadeira)

O conjunto dos números racionais é composto por números que podem ser representados como uma fração, logo, o número misto \(2\frac{3}{4}\) é um número racional.

III. O número \(\sqrt{-2}\) é um número complexo. (Verdadeira)

O conjunto dos números complexos contém os números reais e os números imaginários, que são as raízes de números negativos.