Os números inteiros são os elementos do conjunto Z, formado pelo zero e pelos números positivos e negativos que não possuem parte decimal. Exemplos de números inteiros são -20, -7, -3, 0, 2, 3, 8, 150.
Enquanto os inteiros positivos indicam quantidades inteiras concretas (como três maçãs, vinte dias e dois centímetros), os inteiros negativos representam situações menores que um indicador (como temperaturas abaixo de zero, altitudes abaixo do nível do mar e saldos bancários devedores).
Leia também: Quais são os números irracionais?
Tópicos deste artigo
- 1 - Resumo sobre números inteiros
- 2 - O que são números inteiros?
- 3 - Representação dos números inteiros na reta numérica
- 4 - Conjunto dos números inteiros
- 5 - Subconjuntos dos números inteiros
- 6 - Operações com números inteiros
- 7 - Exercícios resolvidos sobre números inteiros
Resumo sobre números inteiros
- Os inteiros são os números que não possuem parte decimal.
- O conjunto dos números inteiros é representado pela letra Z.
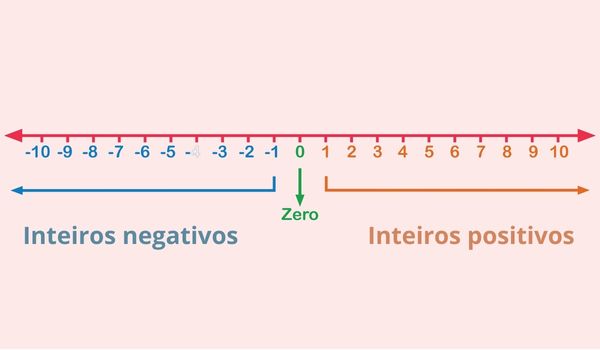
- Os números inteiros se destacam na reta numérica, organizada de modo crescente da esquerda para a direita e com números negativos à esquerda do zero e números positivos à direta do zero.
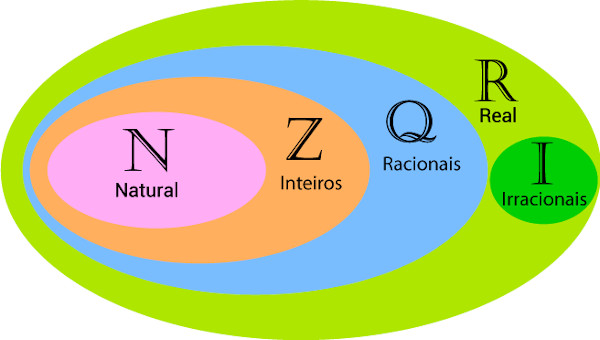
- O conjunto dos números naturais N é o principal subconjunto de Z.
- As operações entre números inteiros segue a regra dos sinais, conhecida também como jogo de sinais.
O que são números inteiros?
Os inteiros são os números que possuem apenas parte inteira, sem a parte decimal, ou seja, são números em que, após a vírgula, há apenas zero. Veja:
3 é um número inteiro.
0 é um número inteiro.
-9 é um número inteiro.
2,5 não é um número inteiro.
9,0000000001 não é um número inteiro.
\(\frac{1}{2}\ =0,5\) não é um número inteiro, pois \(\frac{1}{2}\ =0,5\).
Representação dos números inteiros na reta numérica
A reta numérica é organizada com destaque para os números inteiros. O zero é escrito na posição central e os números positivos e negativos se distribuem à direita e à esquerda respectivamente. Essa distribuição ocorre de modo crescente da esquerda para a direita.

Conjunto dos números inteiros
O conjunto dos números inteiros é expresso pela letra Z. Assim, podemos descrever esse conjunto da seguinte forma:
\(Z=\{\ldots-4,-3,-2,-1,\ 0,\ 1,\ 2,\ 3,\ \ 4\ldots\}\)
Observe que esse conjunto segue infinitamente para a esquerda e para a direita, conforme indicado pelas reticências.
Cabe destacar que cada marcação na reta numérica corresponde a um número inteiro. Assim, por exemplo, o número 0 é inteiro e o número 1 é inteiro, e não há números inteiros entre 0 e 1.
Subconjuntos dos números inteiros
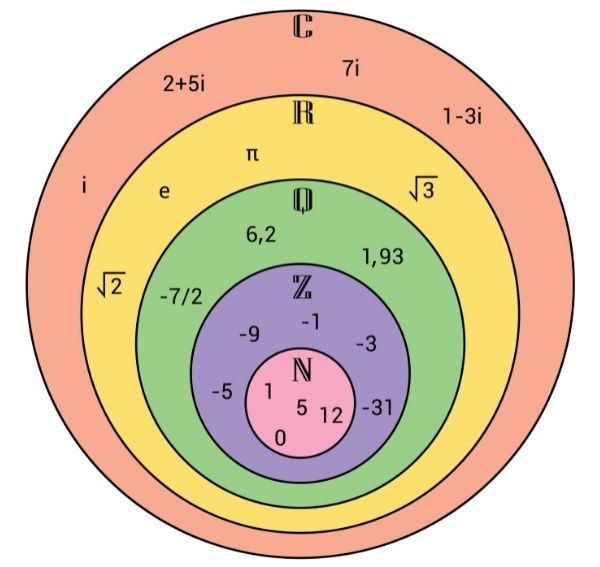
Perceba que os inteiros positivos são elementos de outro conjunto numérico conhecido: o conjunto dos números naturais. Veja:
\(N=\{\ 1,\ 2,\ 3,\ 4,\ 5\ldots\}\)
Assim, o conjunto dos números naturais está contido no conjunto dos números inteiros. Portanto, N é um subconjunto dos números inteiros.
\(N\subset Z\)
Outros subconjuntos dos números inteiros são:
- Z*: conjunto dos números inteiros não nulos.
- Z+: conjunto dos números inteiros positivos.
- Z-: conjunto dos números inteiros negativos.
Operações com números inteiros
Para realizar operações com números inteiros, é fundamental conhecer a regra de sinais (também conhecida como jogo de sinais), que determina o sinal de um resultado com base nos sinais dos termos. Resumidamente, ele segue as seguintes ideias:
- Sinais iguais, resultado positivo:
(+) (+) = +
(–) (–) = +
- Sinais diferentes, resultado negativo:
(–) (+) = –
(+) (–) = –
Vejamos, a seguir, alguns exemplos das operações básicas entre números inteiros.
→ Adição entre números inteiros
\(5+5=10\)
\(-\ 12+(-\ 4)=-16\)
\(-\ 3+7=4\)
\(9+\left(-2\right)=7\)
→ Subtração entre números inteiros
\(3-\ 1=2\)
\(-8-\left(-30\right)=22\)
\(-\ 24\ -\ 5=-29\)
\(14-\left(-3\right)=17\)
→ Multiplicação entre números inteiros
\(2\cdot8=16\)
\(-7\cdot3=-21\)
\(11\cdot-10=\ -110\)
\(-14\ \cdot-1=14\)
→ Divisão entre números inteiros
\(12\div4=3\)
\(25\div-5=-5\)
\(-33\div11=-3\)
\(-70\div-10=7\)
Veja também: Como realizar operações entre conjuntos?
Exercícios resolvidos sobre números inteiros
Questão 1
Considere as afirmações abaixo.
I. Os números inteiros estão contidos nos números naturais.
II. –12∈Z
III. 0 é um número inteiro.
Está correto o que se afirma em
A) I, apenas.
B) II, apenas.
C) III, apenas.
D) I e II, apenas.
E) II e III, apenas.
Resolução:
Alternativa E
I. Os números inteiros estão contidos nos números naturais. (falso)
Z não é subconjunto de N. O número -1, por exemplo, é inteiro, mas não é natural.
II. –12∈Z (verdadeiro)
III. 0 é um número inteiro. (verdadeiro)
Questão 2
Classifique cada afirmação a seguir em V (verdadeira) ou F (falsa):
I. O conjunto {-99, 1, 6,} possui um elemento que não é um número inteiro.
II. Todos os números naturais são inteiros.
III. \(\frac{2}{3}\in Z\)
A ordem correta, de cima para baixo, é
A) F-F-V
B) V-F-F
C) V-V-F
D) V-F-V
E) F-V-F
Resolução
Alternativa E
I. O conjunto {-99, 1, 6,} possui um elemento que não é um número inteiro. (falso)
-99∈Z, 1∈Z e 6∈Z.
II. Todos os números naturais são inteiros. (verdadeiro)
III. \(\frac{2}{3}\in Z\) (falso)
\(\frac{2}{3} \) não é um número inteiro, é um número racional.