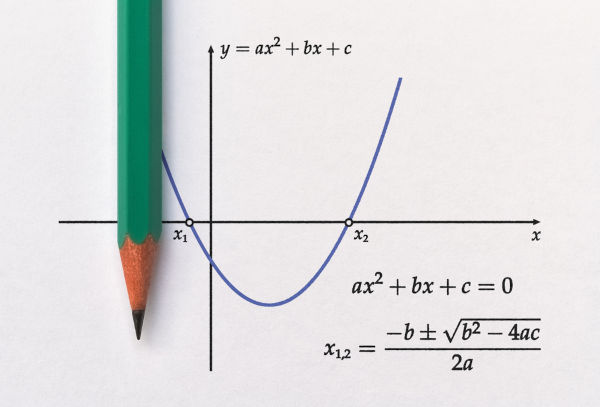
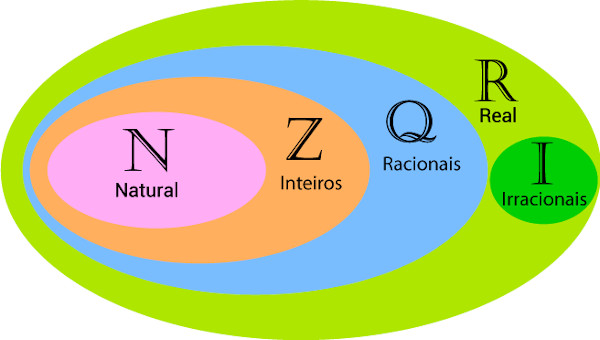
Uma parábola é uma figura geométrica plana que representa o conjunto de pontos de uma função do segundo grau, que, por sua vez, é toda aquela que pode ser escrita na forma: f(x) = ax2 + bx + c, com domínio e contradomínio no conjunto dos números reais. Nessa função, os números representados pelas letras a, b e c pertencem ao conjunto dos reais e são chamados de coeficientes, e a letra x é a variável.
Os coeficientes de uma função do segundo grau ajudam a definir o formato da parábola representada por ela. Especificamente, é o coeficiente a que determina a concavidade de uma parábola.
Concavidade da parábola
Uma função do segundo grau sempre pode ser representada graficamente por uma parábola. Se essa função do segundo grau está na forma discutida acima, sua concavidade deverá ser voltada para cima ou para baixo. O coeficiente a indica isso da seguinte maneira:
Se a > 0, a concavidade está voltada para cima.
Se a < 0, a concavidade está voltada para baixo.
O que é concavidade?
Concavidade é uma palavra usada para representar objetos côncavos, como antenas de televisão, lentes etc. A concavidade é uma reentrância, e o valor do coeficiente a define exatamente para onde essa reentrância aponta.
Nas parábolas, como dito anteriormente, a concavidade está voltada para cima ou para baixo.
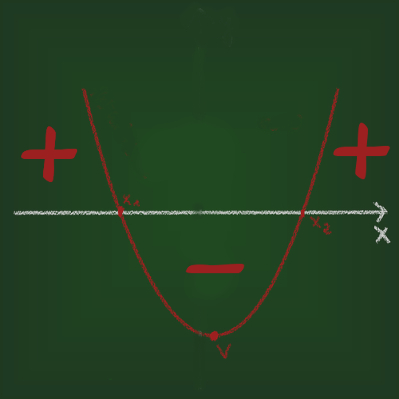
1 – Se a concavidade está voltada para cima:
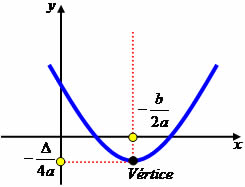
O valor do coeficiente a é positivo, e essa parábola é formada por uma curva que possui um ponto mais baixo do que todos os outros, chamado vértice. No plano cartesiano, isso quer dizer que a menor coordenada y referente a um ponto da função do segundo grau, ou seja, da parábola será a do vértice.
A imagem a seguir mostra uma parábola com concavidade voltada para cima, ou seja, com valor do coeficiente a positivo. O vértice dela é seu ponto de menor valor, também chamado ponto de mínimo.
2 – Se a concavidade está voltada para baixo:
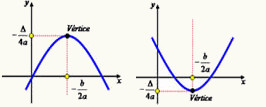
O valor do coeficiente a é negativo nesse caso, e essa parábola é formada por uma curva que possui um ponto mais alto do que todos os outros, chamado vértice. No plano cartesiano, isso quer dizer que a maior valor da coordenada y, referente aos pontos da parábola, será encontrado no vértice.
A imagem a seguir mostra uma parábola com a concavidade voltada para baixo, ou seja, com o coeficiente a negativo. Além disso, também é possível ver o vértice, que é ponto que possui a maior coordenada y possível. Esse ponto também é chamado ponto de máximo.