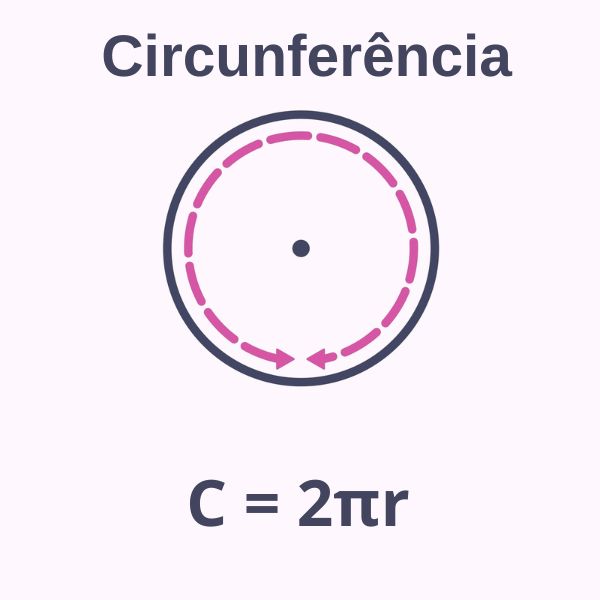
Comprimento da circunferência é o nome que se dá à medida do contorno de um círculo. Para calcular essa medida, usamos como base o valor do raio da figura ou o valor de seu diâmetro, que, como se sabe, equivale ao dobro do comprimento do raio. A fórmula geral usada para calcular o comprimento da circunferência é \(C=2\pi r\).
Leia também: Qual a diferença entre um círculo e uma circunferência?
Tópicos deste artigo
- 1 - Resumo sobre o comprimento da circunferência
- 2 - O que é o comprimento da circunferência?
- 3 - Fórmula para calcular o comprimento da circunferência
- 4 - Como é calculado o comprimento de uma circunferência?
- 5 - Exercícios resolvidos sobre o comprimento da circunferência
Resumo sobre o comprimento da circunferência
- O comprimento da circunferência é a medida do contorno do círculo.
- Para calcular o comprimento da circunferência, basta conhecer a medida do seu raio r.
- O comprimento da circunferência é calculado por C=2πr.
- C → comprimento
- r → raio
- π é uma constante irracional com valor de 3,141592...
O que é o comprimento da circunferência?
Conhecemos como circunferência a curva formada pelo conjunto de pontos que estão a uma mesma distância do seu centro. Essa distância é conhecida como raio. A circunferência é o contorno do círculo, e o comprimento da circunferência é a medida desse contorno.

Como o círculo é uma curva, que não possui lados, então o comprimento do seu contorno não é conhecido como perímetro, mas sim como comprimento da circunferência, logo, o comprimento da circunferência é equivalente ao que conhecemos como perímetro em um polígono. Vale ressaltar que o perímetro é a soma dos lados de um polígono, como a circunferência não possui lados, então não calculamos seu perímetro, mas sim seu comprimento.
Fórmula para calcular o comprimento da circunferência
De modo geral, o comprimento da circunferência é calculado pela fórmula:
\(C=2\pi r\)
C → comprimento da circunferência
r → comprimento do raio da circunferência
π→ constante irracional com valor de, aproximadamente, 3,141592... (conhecido como pi)
O valor de π é um número que não pode ser expresso como uma fração simples, ou seja, é irracional, e possui uma representação decimal infinita e não periódica. Ele é frequentemente utilizado para resolver problemas envolvendo figuras arredondadas, como circunferências, esferas, cilindros, arcos e cones. A letra π é utilizada para representar esse valor por este ter um número infinito de casas decimais, sendo algumas delas: π = 3,141592653589...
Dado que π possui infinitas casas decimais, aproximamos seu valor para resolver os problemas matemáticos que envolvem sua utilização. Essas aproximações são escolhidas de acordo com o grau de precisão necessário para cada problema, sendo as mais comuns π = 3, π = 3,1 ou π = 3,14.
Outra forma de calcular o comprimento da circunferência é utilizando o seu diâmetro, pois sabemos que o comprimento do diâmetro é igual ao dobro do comprimento do raio, sendo assim, podemos calcular o comprimento da circunferência com a fórmula:
\(C=d\pi\)
Em que d é o diâmetro da circunferência.
Note que as duas fórmulas dizem a mesma coisa, uma delas utiliza o diâmetro e a outra utiliza o raio multiplicado por 2.
Veja também: Como calcular a distância entre duas circunferências?
Como é calculado o comprimento de uma circunferência?
Para calcular o comprimento da circunferência, basta substituirmos o valor do raio da circunferência e, caso seja necessário, utilizar uma aproximação para o valor de π. O uso da aproximação para o valor de π depende do objetivo para o qual estamos calculando o valor do comprimento da circunferência, quanto mais casas decimais considerarmos, mais precisos serão os dados. Em alguns casos, não utilizamos aproximação para π, deixando o próprio símbolo.
Exemplo 1:
Qual é o comprimento de uma circunferência que possui raio medindo 12 cm?
Resolução:
Como não temos aproximação para π, substituiremos somente r = 12 na fórmula:
\(C=2\pi r\)
\(C=2\cdot\pi\cdot12\ \)
\(C=24\pi\ cm\)
Exemplo 2:
Uma área de lazer de um condomínio possui comprimento de área no formato de um círculo de raio medindo 5 metros. Utilizando π = 3,1, o comprimento da circunferência desse círculo mede quanto?
Resolução:
Calculando o comprimento da circunferência, temos que:
r = 5
π=3,1
\(C=2\pi r\)
\(C=2\cdot3,1\cdot5\)
\(C=6,2\cdot5\)
\(C=31\ m\ \)
Exemplo 3:
Uma circunferência possui comprimento medindo 12 cm. Considerando π = 3, qual medida do diâmetro dessa circunferência?
Resolução:
Sabemos que:
\(C=2\pi r\)
Logo, temos que:
\(12=2\cdot3\cdot r\)
\(12=6r\)
\(\frac{12}{6}=r\)
\(r=2\)
Se o raio mede 2 cm, então o diâmetro mede 4 cm.
Saiba mais: Como descobrir qual é a área de um triângulo?
Exercícios resolvidos sobre o comprimento da circunferência
Questão 1
Em uma piscina no formato circular com raio medindo 2 metros, será colocada uma grade de proteção, de modo que ela tenha sempre 1 metro de distância da borda da piscina. Utilizando 3,14 como aproximação para π, a medida do comprimento dessa grade é de:
A) 15,90 cm
B) 18,84 cm
C) 23,12 cm
D) 25,04 cm
E) 28,28 cm
Resolução:
Alternativa B
Para calcular o comprimento, temos que r = 2 + 1 = 3 e que π = 3,14:
\(C=2\ \pi r\)
\(C=2\cdot3,14\cdot3\)
\(C=6,28\cdot3\)
\(C=18,84\ cm\)
Questão 2
Conhecemos como arco uma parte do comprimento da circunferência. Analisando a imagem a seguir, podemos perceber que temos um arco BC cujo ângulo central é de 90º.
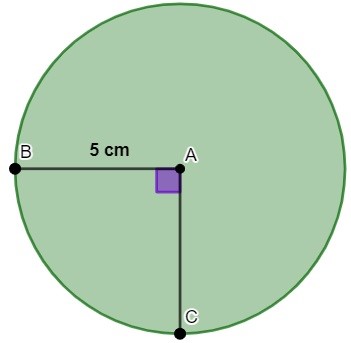
Analisando a circunferência, podemos afirmar que diferença entre o comprimento da circunferência e o comprimento do arco BC é igual a:
A) 5π
B) 7,5π
C) 10π
D) 12,5π
E) 17π
Resolução:
Alternativa B
Primeiro calcularemos o comprimento da circunferência:
\(C=2\pi r\)
\(C=2\pi\cdot5\)
\(C=10\pi\)
Sabemos que a circunferência representa uma volta completa, que é 360º, logo, dividindo 360º por 90º, temos que:
360 : 90 = 4
Então essa é a quarta parte da circunferência. Dividindo o comprimento por 4, encontraremos a medida do arco AC:
\(C∶4=10\pi∶4=2,5\pi\ \)
Sendo assim, a diferença será de:
\(10\pi-2,5\pi=7,5\pi\)
Fontes
Lima, Elon Lages. Matemática: volume único. Rio de Janeiro: IMPA, SBM, 2009.
Giovanni, José Ruy; Bonjorno, José Roberto. Matemática: ensino médio - volume único. São Paulo: FTD, 2006.