Triângulo retângulo é o que possui um de seus ângulos internos medindo 90°, ou seja, um ângulo reto. O triângulo é o polígono mais estudado na geometria plana, principalmente o triângulo retângulo, que possui relações específicas entre os seus lados e ângulos. Uma dessas relações é o teorema de Pitágoras, que demonstra uma relação entre os lados dessa figura.
Além do teorema de Pitágoras, existem outras relações importantes, como as relações métricas e a trigonometria, com as razões trigonométricas seno, cosseno e tangente, no triângulo retângulo. Ele possui uma fórmula para o cálculo da sua área, que é a mesma utilizada para outros triângulos. Para calcular o seu perímetro, basta realizar a soma dos seus lados.
Leia mais: Relações fundamentais da trigonometria — igualdades pelas quais se relaciona as razões: seno, cosseno e tangente
Tópicos deste artigo
- 1 - Resumo sobre triângulo retângulo
- 2 - Características do triângulo retângulo
- 3 - Perímetro do triângulo retângulo
- 4 - Área do triângulo retângulo
- 5 - Teorema de Pitágoras
- 6 - Trigonometria no triângulo retângulo
- 7 - Relações métricas no triângulo retângulo
- 8 - Exercícios resolvidos sobre triângulo retângulo
Resumo sobre triângulo retângulo
-
É o triângulo que possui um ângulo interno de 90°, ou seja, um ângulo reto.
-
O teorema de Pitágoras é uma relação entre os lados do triângulo retângulo.
-
Para calcular sua área, multiplicamos a sua base pela sua altura e dividimos por 2.
-
Para encontrar o comprimento de lados desconhecidos nele, podemos usar também as relações métricas e a trigonometria.
Características do triângulo retângulo
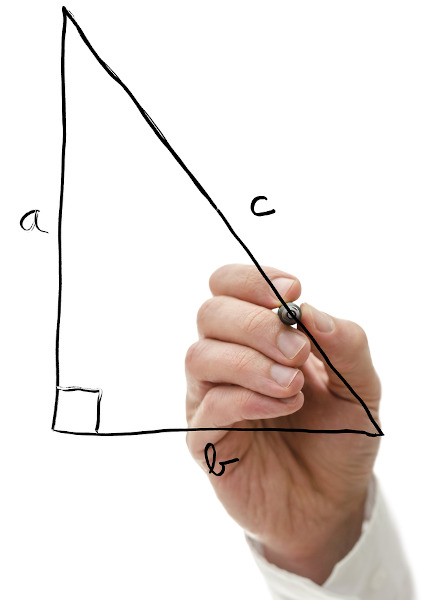
O triângulo retângulo é um polígono de três lados e três ângulos que possui um de seus ângulos internos medindo 90°, ou seja, ele é reto. Com isso, os demais ângulos são agudos, ou seja, menores que 90°. Em um triângulo, o maior lado, que fica sempre oposto ao ângulo de 90º, recebe o nome de hipotenusa, e os demais lados são conhecidos como catetos.
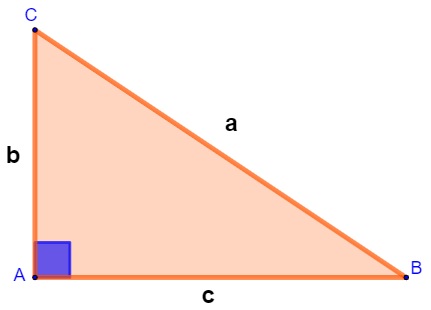
-
O ângulo CAB é de 90°.
-
O lado CB é a hipotenusa de comprimento a.
-
Os lados AC e AB são os catetos, com comprimentos representados por b e c.
Caso queira saber mais sobre o tema deste tópico, leia: Os componentes do triângulo retângulo.
Perímetro do triângulo retângulo
Assim como os demais polígonos, no triângulo retângulo, o perímetro é a soma do comprimento de todos os seus lados. Então, dado o triângulo retângulo com lados medindo a, b e c, seu comprimento será calculado por:
|
P = a + b + c |
Área do triângulo retângulo
Em um triângulo qualquer, para calcular a sua área, multiplicamos a sua base pela altura e dividimos por 2. A única peculiaridade que o triângulo retângulo tem, quando comparado aos demais triângulos, é que a sua altura coincide com um dos seus catetos, pois sabemos que os catetos formam um ângulo reto entre eles. Então, para calcular a área do triângulo de hipotenusa de comprimento a e catetos de comprimento b e c, utilizamos a fórmula:
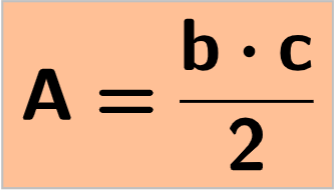
Exemplo: dado um triângulo retângulo, de lados medindo 20 cm, 21 cm e 29 cm, o seu perímetro e a sua área terão que valor?
Resolução:
Começando pelo perímetro, sabemos que:
P = 29 + 21 + 20 = 60 cm
Agora, para calcular a área, sabemos que o maior lado é a hipotenusa, logo, vamos fazer o cálculo utilizando os outros dois lados, que medem 21 cm e 20 cm cada, então, temos que:
![]()
Desse modo, a área será de 210 cm².
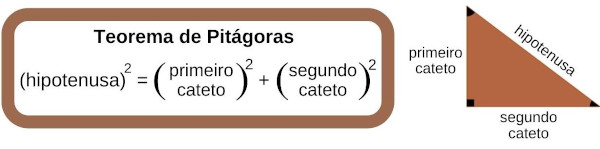
Teorema de Pitágoras
O teorema de Pitágoras é uma relação entre os lados de um triângulo retângulo. O teorema diz que a hipotenusa ao quadrado é igual à soma do quadrado dos catetos. Dado um triângulo retângulo de hipotenusa a e catetos b e c, temos que:
|
a² = b² + c² |
Exemplo: encontre o valor de x no triângulo retângulo a seguir.
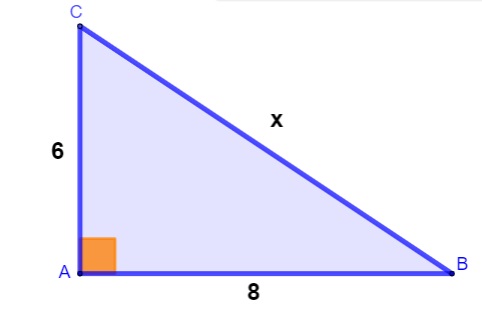
Resolução:
Aplicando o teorema de Pitágoras, temos que:
x² = 6² + 8²
x² = 36 + 64
x² = 100
x = √100
x = 10
-
Videoaula sobre teorema de Pitágoras
Trigonometria no triângulo retângulo
A trigonometria no triângulo retângulo é uma área da matemática que estuda a relação entre os lados e os ângulos de um triângulo retângulo. Nesse estudo, aprende-se que as razões trigonométricas são seno, cosseno e tangente, que são as razões entre os lados do triângulo. Antes de conhecer cada uma delas, é importante compreender o que são os catetos adjacente e oposto de um ângulo.
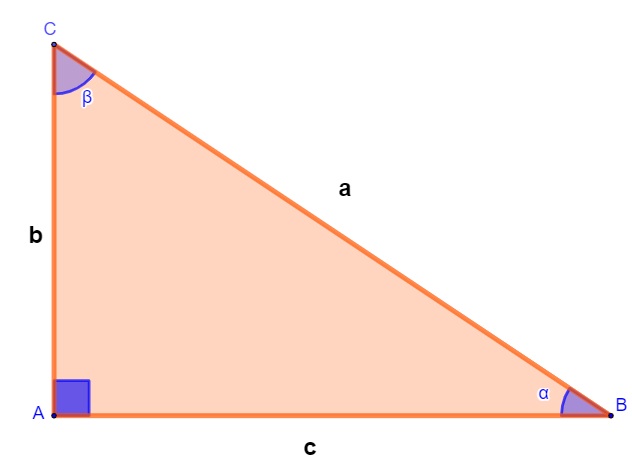
Sabemos que a hipotenusa é o lado oposto ao ângulo de 90°, no caso, é o segmento BC. Os lados AB e AC são conhecidos como catetos, e, dependendo do ângulo, pode se tratar de um cateto oposto a ele ou um cateto adjacente a ele.
No ângulo α, o lado AC é o cateto oposto ao ângulo (pois está de frente ao ângulo), e o lado AB é o cateto adjacente ao ângulo (pois é um dos segmentos que formam o ângulo).
No ângulo β, o lado AB é o cateto oposto a ele (pois está de frente ao ângulo), e o lado AC é o cateto adjacente a ele (pois é um dos segmentos que formam o ângulo).
As razões seno, cosseno e tangente são:
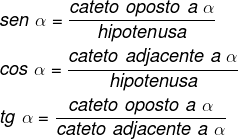
Utilizamos as razões trigonométricas para encontrar o comprimento de lados desconhecidos do triângulo retângulo. Para tanto, veja a tabela com o valor do seno, cosseno e tangente dos ângulos notáveis, de 30°, 45° e 60°.
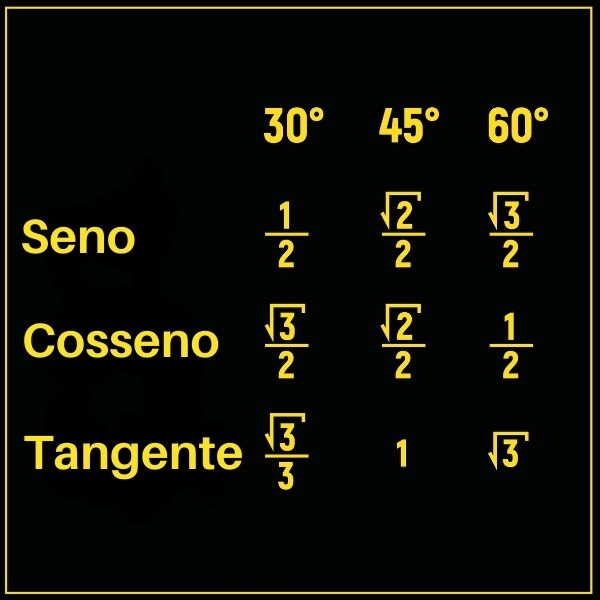
Conhecendo o valor das razões trigonométricas do triângulo, dados um lado e um ângulo notável, é possível encontrar todos os lados de um triângulo retângulo com base na trigonometria.
Exemplo: encontre o valor de x.
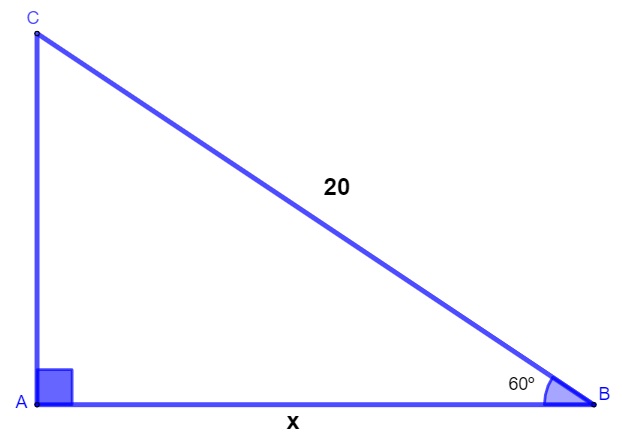
Queremos encontrar o valor x, sendo que x é o cateto adjacente ao ângulo B, e conhecemos também o valor da hipotenusa desse triângulo, então a razão trigonométrica que relaciona o cateto adjacente com a hipotenusa é o cosseno. Sabendo que o cosseno de 60° é igual a 1/2, temos que:
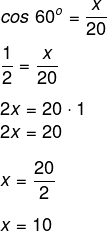
Relações métricas no triângulo retângulo
As relações métricas, como o nome sugere, são fórmulas que relacionam os segmentos de um triângulo retângulo.
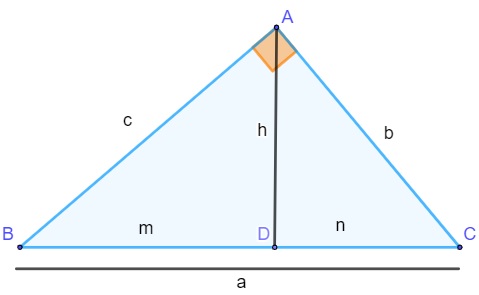
As relações métricas são:
a² = c² + b²
b² = a · n
c² = a · m
h² = m · n
a = m + n
a · h = b · c
-
Videoaula sobre relações métricas no triângulo retângulo
Exercícios resolvidos sobre triângulo retângulo
Questão 1
Um terreno possui o formato de um retângulo de lados medindo 20 m e 21 m. Esse terreno será divido ao meio entre dois irmãos, Caio e Cauan. Caso Caio decida cercar a sua parte do terreno, o perímetro dela terá:
A) 60 metros
B) 55 metros
C) 41 metros
D) 38 metros
E) 35 metros
Resolução:
Alternativa A
Sabendo que esse terreno possui formato de retângulo, se traçarmos a sua diagonal, ele será dividido em dois triângulos retângulos. Para calcular o comprimento da diagonal, basta aplicar o teorema de Pitágoras:
d² = 20² + 21²
d² = 400 + 441
d² = 841
d = √841
d = 29 m
Conhecendo o comprimento da diagonal, para encontrar seu perímetro, temos que:
P = 20 + 21 + 29 = 60 metros
Questão 2
(Enem) Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista, na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.
Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.
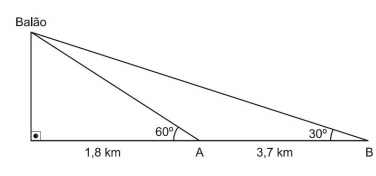
Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°. Qual a altura aproximada em que se encontrava o balão?
A) 1,8 km
B) 1,9 km
C) 3,1 km
D) 3,7 km
E) 5,5 km
Resolução:
Alternativa C
Analisando a imagem, podemos perceber que a altura h pode ser dada pela tangente de 60º.
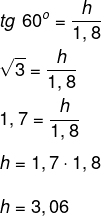
Assim, a altura é de aproximadamente 3,1 km.