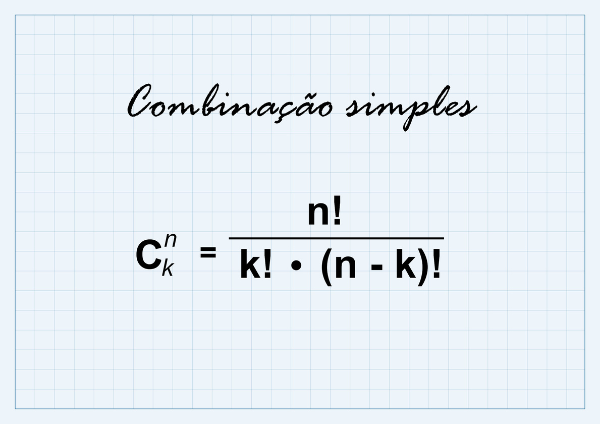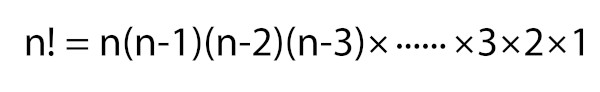Combinação simples é um agrupamento de k elementos distintos e não ordenados escolhidos a partir de n elementos. Em uma sala de aula, por exemplo, é comum criar grupos para realizar as atividades. Assim, n seria o total de alunos na sala e k seria a quantidade de alunos em cada grupo. Aplicando a fórmula da combinação simples, podemos descobrir de quantas maneiras é possível formar um grupo de k alunos a partir de n alunos.
Leia também: Temas de análise combinatória que caem no Enem
Tópicos deste artigo
- 1 - Resumo sobre combinação simples
- 2 - O que é combinação simples?
- 3 - Qual a fórmula da combinação simples?
- 4 - Como calcular uma combinação simples?
- 5 - Qual a diferença entre combinação simples e arranjo simples?
- 6 - Exercícios resolvidos sobre combinação simples
Resumo sobre combinação simples
-
Uma combinação simples é um método de contagem em que os agrupamentos de elementos distintos se diferem apenas pela natureza, e não pela ordem. Assim, não há diferença entre (X, Y) e (Y, X).
-
A fórmula para descobrir quantas combinações de n elementos distintos tomados k a k são possíveis é
\(C_k^n=\frac{n!}{k!⋅(n-k)!}\)
-
Em um arranjo simples, uma alteração na ordem dos elementos produz um agrupamento diferente.
O que é combinação simples?
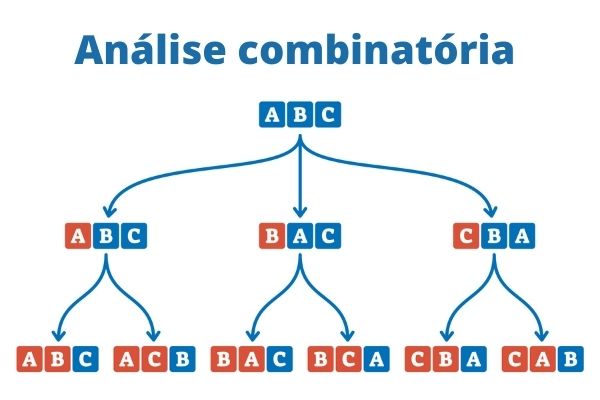
A análise combinatória estuda métodos de contagem. Entre esses métodos, há a combinação, que considera agrupamentos em que a ordem dos elementos não é relevante. Uma combinação é chamada de simples quando os elementos do grupo são distintos. Vejamos um exemplo para ilustrar essa ideia:
Imagine que 3 alunos, em uma turma de 20, devem ser escolhidos para formar um comitê de formatura. Vamos representar os alunos dessa turma pelas letras de A até T. Perceba que escolher os alunos A, B e C para compor a comissão é exatamente a mesma coisa que escolher os alunos B, C e A. Em outras palavras, a ordem dos elementos não altera o agrupamento. Assim, ABC é uma possível combinação de 3 alunos escolhidos a partir de 20 alunos.
Observação: empregamos a letra n para indicar o número total de elementos e a letra k (ou p em alguns textos) para fazer referência à quantidade de elementos em cada agrupamento.
Qual a fórmula da combinação simples?
A fórmula da combinação simples é utilizada para encontrar quantos agrupamentos não ordenados de n elementos distintos tomados k a k são possíveis.
Nessas condições, a fórmula da combinação simples é
\(\mathbf{C_k^n=\frac{n!}{k!⋅(n-k)!}}\)
em que \(1≤ k ≤ n\). Lembre-se de que o símbolo ! indica o fatorial do respectivo termo .
Observação: outras maneiras de representar \(C_k^n\) são \(C_{n,k}\) e \(({^n_k})\).
Vejamos alguns exemplos de como aplicar essa fórmula.
-
Exemplo 1: Considere o conjunto {r,s,t}. Quantas combinações simples de 2 elementos são possíveis a partir do conjunto dado?
Primeiro, vamos encontrar explicitamente as combinações:
\(\{r,s\},\{r,t\},\{s,t\}\)
Agora, vamos verificar a resposta aplicando a fórmula. Note que, nesse caso, n = 3 e k = 2.
\(C_2^3=\frac{3!}{2!⋅(3-2)!}\)
\(C_2^3=\frac{6}{2⋅1}\)
\(C_2^3=3\)
-
Exemplo 2: Quantas combinações simples de 8 elementos em grupos de 5 elementos são possíveis?
Como a quantidade de elementos é maior, nessa situação é mais vantajoso aplicar diretamente a fórmula. Como n = 8 e k = 5, temos que
\(C_5^8=\frac{8!}{5!⋅(8-5)!}\)
\(C_5^8=\frac{8⋅7⋅6⋅5!}{5!⋅3!}\)
\(C_5^8=\frac{8⋅7⋅6}6\)
\(C_5^8=56\)
Veja também: O que é combinação com repetição?
Como calcular uma combinação simples?
Em todo contexto que envolva problemas de contagem, é necessário interpretar a situação dada e aplicar a ferramenta correta. Se os elementos envolvidos são distintos e a ordem não altera a composição dos agrupamentos, então trata-se de uma combinação simples. A partir daí, devemos identificar os valores de n e k e utilizar a fórmula correspondente.
-
Exemplo 1: De quantas maneiras podemos formar uma comissão de 3 alunos a partir de uma turma de 20 alunos?
Conforme verificamos no início do texto, esse exemplo é uma combinação simples com n = 20 e k = 3. Portanto,
\(C_3^{20}=\frac{20!}{3!⋅(20-3)!}\)
\(C_3^{20}=\frac{20 ⋅19 ⋅ 18 ⋅ 17!}{3!⋅17!}\)
\(C_3^{20}=\frac{20 ⋅19 ⋅ 18}6\)
\(C_3^{20}=1140\)
-
Exemplo 2: Um mural será pintado com 5 cores diferentes. De quantas formas é possível escolher essas cores a partir de um catálogo com 9 opções?
Note que as cores são distintas e a ordem de seleção não é relevante para o contexto do problema. Assim, temos uma combinação simples com n = 9 e k = 5. Logo,
\(C_5^9=\frac{9!}{5!⋅(9-5)!}\)
\(C_5^9=\frac{9 ⋅ 8 ⋅ 7⋅ 6⋅ 5!}{5!⋅4!}\)
\(C_5^9=\frac{9 ⋅ 8 ⋅ 7⋅ 6}{4⋅3⋅2⋅1}\)
\(C_5^9=126\)
Saiba mais: Qual é o princípio fundamental da contagem?
Qual a diferença entre combinação simples e arranjo simples?
A diferença entre combinação e arranjo simples é que no arranjo, a ordem é relevante na composição dos agrupamentos.
Considere uma competição olímpica que será disputada por 7 atletas. O pódio é formado por três posições: medalhista de ouro, de prata e de bronze. Perceba que, nesse caso, a ordem de vitórias influencia no resultado. Ou seja, o atleta A receber medalha de ouro; o B, medalha de prata; e o C, medalha de bronze é uma situação diferente de o atleta B receber medalha de ouro; o C, medalha de prata; e o A, de bronze. Esse é um exemplo de arranjo simples. Para saber mais sobre arranjo simples, clique aqui.
-
Videoaula sobre a diferença entre arranjo simples e combinação simples
Exercícios resolvidos sobre combinação simples
Questão 1
(Enem) A prefeitura de uma cidade está renovando os canteiros de flores de suas praças. Entre as possíveis variedades que poderiam ser plantadas, foram escolhidas cinco: amor-perfeito, cravina, petúnia, margarida e lírio. Em cada um dos canteiros, todos com composições diferentes, serão utilizadas somente três variedades distintas, não importando como elas serão dispostas.
Um funcionário deve determinar os trios de variedades de flores que irão compor cada canteiro.
De acordo com o disposto, a quantidade de trios possíveis é dada por
a) 5
b) \( 5⋅3\)
c) \(\frac{5!}{(5-3)!}\)
d) \(\frac{5!}{(5-3)!2!}\)
e) \(\frac{5!}{(5-3)!3!}\)
Resolução
De acordo com as informações, cada canteiro será composto por 3 tipos distintos de flores, e há 5 tipos para escolher. Além disso, não importa a disposição das flores, ou seja, a ordem é irrelevante. Portanto, trata-se de uma combinação simples com n = 5 e k = 3, e a quantidade de trios possíveis é dada por
\(C_3^5=\frac{5!}{3!(5-3)!}\)
Alternativa E.
Questão 2
(PUC) Uma companhia de teatro lírico é formada por cinco sopranos e seis tenores. Para uma das cenas de uma ópera, o diretor precisa de cinco cantores, sendo três sopranos e dois tenores.
Então, o número de possibilidades para a escolha dos participantes dessa cena é
a) 150
b) 462
c) 1800
d) 7200
e) 55440
Resolução
A escolha dos sopranos independe da ordem de seleção. Assim, trata-se de combinação simples com n = 5 e k = 3.
\(C_3^5=\frac{5!}{3!⋅(5-3)!}\)
\(C_3^5=\frac{5 ⋅ 4 ⋅ 3!}{3! 2!}\)
\(C_3^5=10\)
A escolha dos tenores independe da ordem de seleção. Assim, trata-se de combinação simples com n = 6 e k = 2.
\(C_2^6=\frac{6!}{2!⋅(6-2)!}\)
\(C_2^6=\frac{6⋅5⋅4!}{2!⋅4!}\)
\(C_2^6=15\)
Portanto, pelo princípio multiplicativo, a escolha de todos os participantes dessa cena é
\(C_3^5⋅C_2^6=10⋅15 = 150\)
Alternativa A.
Fontes
BEZERRA, Nazaré. Análise combinatória e probabilidade. Belém: EditAedi, 2018. E-book (198 p.). Disponível em: http://livroaberto.ufpa.br/jspui/handle/prefix/480.
DURO, M. L. Análise combinatória e construção de possibilidades: o raciocínio formal no ensino médio. Dissertação (Mestrado em Educação) – Faculdade de Educação, Universidade Federal do Rio Grande do Sul. Disponível em: http://hdl.handle.net/10183/49729.