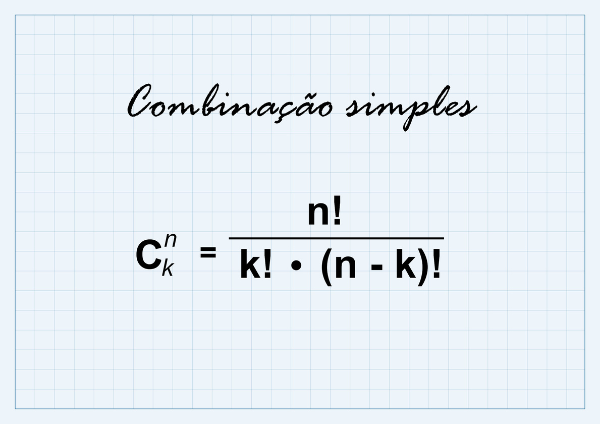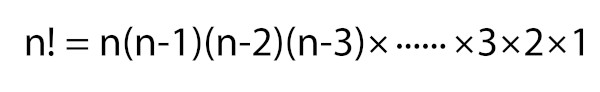A combinação com repetição, conhecida também como combinação completa, é um tipo de agrupamento estudado na análise combinatória, que, por sua vez, é a área da Matemática responsável por desenvolver técnicas de contagem para várias situações diferentes de agrupamento. Dado um conjunto com n elementos, conhecemos como combinação com repetição todos os subconjuntos formados com k elementos entre os n elementos do conjunto.
A diferença entre a combinação simples e a combinação completa é que, na simples, os elementos são necessariamente distintos. Para encontrar a quantidade de combinações com repetição, existe uma fórmula específica.
Leia também: Análise combinatória no Enem: como esse tema é cobrado?
Tópicos deste artigo
- 1 - O que é a combinação com repetição?
- 2 - Fórmula da combinação com repetição
- 3 - Como calcular o número de combinações com repetição?
- 4 - Exercícios resolvidos
O que é a combinação com repetição?

A análise combinatória é a área da Matemática que estuda maneiras para realizar a contagem de agrupamentos possíveis em determinadas situações. Entre esses agrupamentos, existe um que é conhecido como combinação com repetição. Dado um conjunto com n elementos, vamos contar a quantidade de agrupamentos não ordenados que podemos formar escolhendo k elementos dentre esses n elementos, sabendo que um mesmo elemento pode ser escolhido mais de uma vez.
Exemplo:
Uma revendedora de cosméticos organizou uma promoção para vender batons. Os clientes que comprarem dois batons ganharão o terceiro. Sabendo que as cores disponíveis são rosa, vermelho, preto, marrom e coral, existem diferentes maneiras de um cliente escolher esses três batons. Vamos, então, pensar nos agrupamentos possíveis para os três batons.
Nesse caso, a ordem não é importante, ou seja, os agrupamentos não são ordenados, pois, se um cliente escolher vermelho, coral e marrom, e o outro escolher marrom, coral e vermelho, ambos terão os mesmos batons, o que torna esse problema uma combinação.
Perceba também que não existe restrição que faça com que os batons tenham que ser de cores distintas, logo um cliente pode comprar três batons vermelhos, por exemplo, ou dois pretos e um coral, enfim, pode haver repetição, o que evidencia que essa situação se trata de uma combinação com repetição. Veja a seguir como calcular essa combinação com repetição.
Leia também: Como calcular permutações com repetição?
Fórmula da combinação com repetição
Dado um conjunto com n elementos tomados de k a k, para calcular a quantidade de combinações com repetição, utilizamos a seguinte fórmula:
![]()
CR → combinação com repetição.
Existe outra fórmula para a combinação com repetição que a relaciona com uma combinação simples:
![]()
Como calcular o número de combinações com repetição?
Vejamos agora a aplicação da fórmula na situação proposta anteriormente, ou seja, tendo 5 opções de cores de batons (rosa, vermelho, preto, coral e marrom), de quantas maneiras distintas podemos montar um kit com 3 batons?
Queremos calcular a combinação com repetição com 5 elementos tomados de 3 em 3:
n → 5
k → 3
Substituindo na fórmula, temos que:
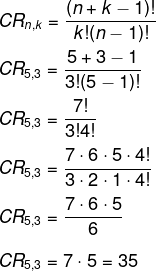
Exercícios resolvidos
Questão 1 - Uma lanchonete oferece 4 tipos de salgados. Qual é o número de maneiras que um cliente pode escolher 6 salgados?
A) 62
B) 54
C) 504
D) 84
E) 98
Resolução
Alternativa D.
Nesse caso, a ordem não é importante, o que faz com que esse seja um problema de combinação. Além disso, não há restrição quanto a repetições, pois estamos resolvendo uma combinação com repetição. Aplicando a fórmula, temos que:
n → 4
k → 6
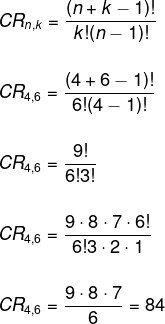
Questão 2 - (Enem 2017) Um brinquedo infantil caminhão-cegonha é formado por uma carreta e dez carrinhos nela transportados, conforme a figura.
No setor de produção da empresa que fabrica esse brinquedo, é feita a pintura de todos os carrinhos para que o aspecto do brinquedo fique mais atraente. São utilizadas as cores amarelo, branco, laranja e verde, e cada carrinho é pintado apenas com uma cor. O caminhão-cegonha tem uma cor fixa. A empresa determinou que em todo caminhão-cegonha deve haver pelo menos um carrinho de cada uma das quatro cores disponíveis. Mudança de posição dos carrinhos no caminhão-cegonha não gera um novo modelo do brinquedo.
Com base nessas informações, quantos são os modelos distintos do brinquedo caminhão-cegonha que essa empresa poderá produzir?
A) C6,4
B) C9,3
C) C10,4
D) 64
E) 46
Resolução
Alternativa B.
Note que temos uma combinação com repetição de 4 opções de cores: n = 4 para 6 carrinhos k = 6. Porém, nas alternativas, temos combinações simples como resposta, então vamos utilizar a fórmula que transforma uma combinação com repetição em uma combinação simples.
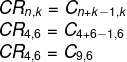
Note que não existe essa alternativa, porém existe a alternativa simétrica a ela, a combinação Cn,k = Cn,n-k. Veja que 9 – 6 = 3, logo a combinação C9,6 tem o mesmo valor que a combinação C9,3, o que torna a alternativa b a correta.