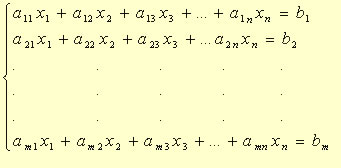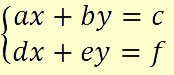Vamos abordar a classificação de um sistema de duas equações do 1º grau com duas incógnitas. Ao resolver os sistemas pelo método da adição ou da substituição, verificaremos três condições de classificação:
Sistema Determinado – SD
Sistema Possível Indeterminado – SID
Sistema Impossível – SI
Sistema Determinado
Um sistema de equações é considerado determinado quando apresenta uma única solução, isto é, no caso de um sistema de duas equações do 1º grau com duas incógnitas, há um único par ordenado. Observe:
Ao resolvermos o sistema 
, obtemos uma única possível solução: (4, 3).
Sistema Possível Indeterminado
Esse sistema admite infinitas soluções, isto é, temos infinitos pares ordenados (x, y) que satisfazem ao sistema. Observe o sistema 
, ele possui infinitas soluções.
Observe que quando temos 0y = 0, podemos considerar qualquer valor para y que mesmo assim, a igualdade se mantém verdadeira.
Sistema Impossível
Nesse sistema dizemos que não existem soluções possíveis, isto é, ele não possui par ordenado que satisfaça à condição do sistema de equações. Na resolução do sistema ocorre uma condição inexistente na Matemática. Observe:
