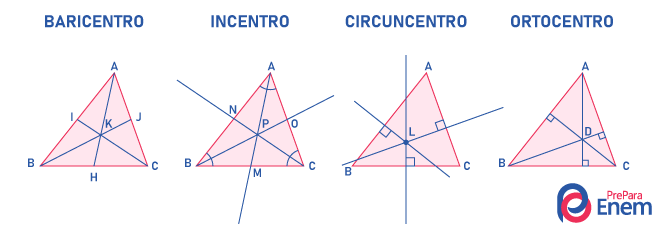
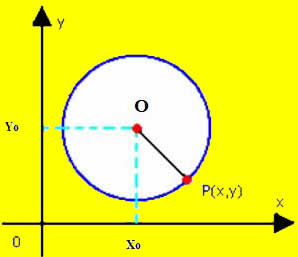
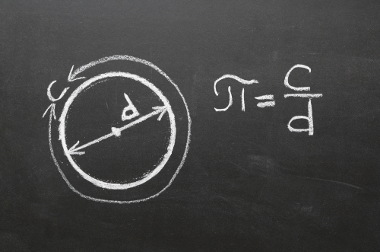Circunferência é uma figura da geometria plana bastante comum no nosso cotidiano. Ela é o conjunto de pontos que estão a uma mesma distância r do centro, esse r é conhecido como raio da circunferência. A circunferência possui alguns elementos em si, como a corda, o centro, o diâmetro e o raio.
É importante destacar que círculo e circunferência são coisas diferentes, pois o primeiro é a região delimitada por uma circunferência, já o segundo é apenas o contorno do círculo. Existem fórmulas específicas para calcular-se a área de um círculo e o comprimento da circunferência. Na geometria analítica, é possível encontrar-se a equação geral e a equação reduzida de uma circunferência.
Leia também: Quais são as possíveis posições entre duas circunferências?
Tópicos deste artigo
- 1 - Elementos da circunferência
- 2 - Diferença entre círculo e circunferência
- 3 - Comprimento de circunferência
- 4 - Área da circunferência
- 5 - Equação reduzida da circunferência
- 6 - Equação geral da circunferência
- 7 - Exercícios resolvidos
Elementos da circunferência
A circunferência possui elementos importantes, sendo eles o raio r, o centro C, o diâmetro d e as cordas.

-
Centro e raio
Para construir-se uma circunferência, seu centro, como o nome sugere, é o ponto que está no meio e a uma mesma distância da figura. O raio denotado por r é qualquer seguimento de reta que parte do centro e vai até a circunferência. A distância r é de grande importância para calcular-se a área e o comprimento da figura.
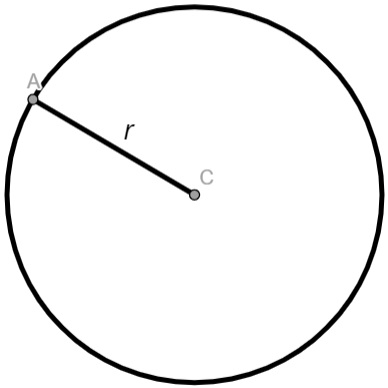
C → Centro da circunferência
r → raio da circunferência
-
Diâmetro e corda
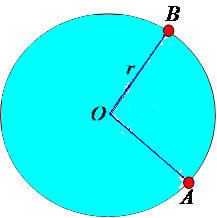
A corda é um seguimento de reta que possui as duas extremidades na circunferência, e o diâmetro é qualquer corda que passa pelo centro.
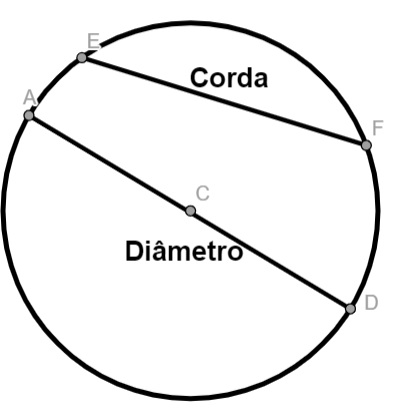
Vale ressaltar que o comprimento do diâmetro é igual a duas vezes o comprimento do raio, ou seja:
d = 2r
Diferença entre círculo e circunferência
Como discutimos, a circunferência é formada por todos os pontos que estão a uma mesma distância r do centro, e o círculo é a região delimitada pela circunferência, ou seja, a circunferência é o contorno e o círculo é a região que está dentro do contorno.
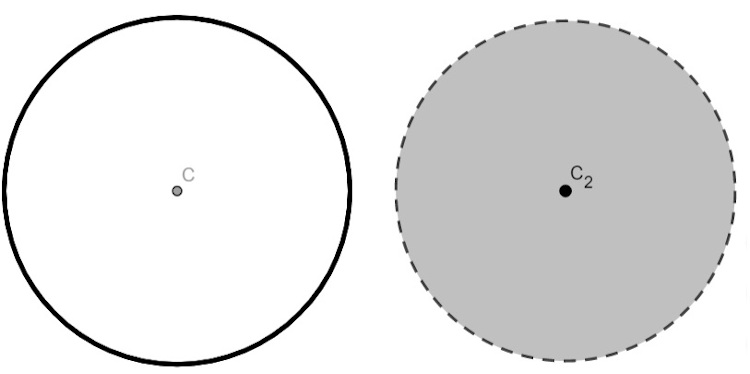
Veja mais: Circunferência e círculo: definições e diferenças básicas
Comprimento de circunferência
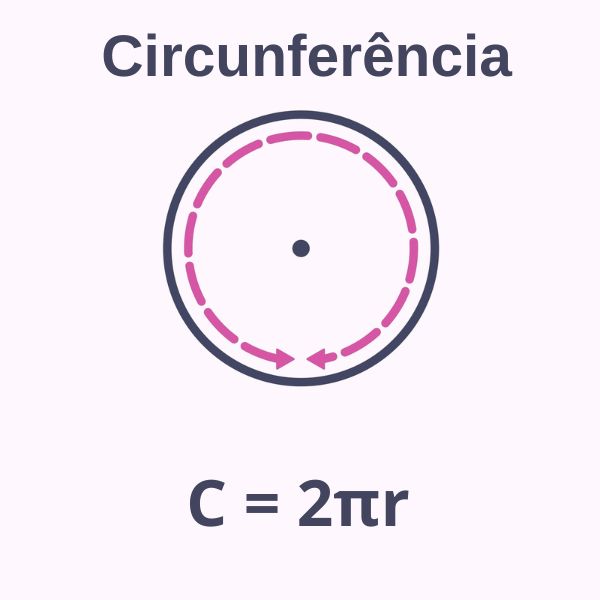
O comprimento da circunferência é a medida do seu contorno, muitas vezes chamada de perímetro, no entanto, como a circunferência não é um polígono, não utilizamos o termo perímetro, e sim comprimento.
|
C = 2·π·r |
C → comprimento
r → raio
π → (lê-se: pi)
Observação: O π é um número irracional bastante antigo e foi estudado por vários povos. Ele é representado dessa maneira, por uma letra grega, pelo fato de ser um número irracional, ou seja, uma dízima não periódica. Veja alguns dígitos do número π.
π = 3,14159265358979...
Em questões de provas e vestibulares com problemas envolvendo o π, é bastante comum que o enunciado dê a aproximação dele, geralmente, utilizando, no máximo, duas casas decimais, ou seja, 3,14. Ainda, é comum também a utilização de nenhuma casa decimal, ou seja, π = 3, ou somente uma, π = 3,1. Cabe à questão informar qual valor deve ser usado, ou, quando esse valor não for informado, podemos utilizar apenas o símbolo π.
Exemplo 1:
Calcule o comprimento da circunferência que possui raio igual a 5 cm (use π = 3,1).
C = 2· π · r
C = 2 · 3,1 · 5
C = 6,2 · 5
C = 31 cm
Exemplo 2:
Calcule o comprimento da circunferência a seguir, sabendo que o seguimento AE possui 14 cm (use π = 3,1).
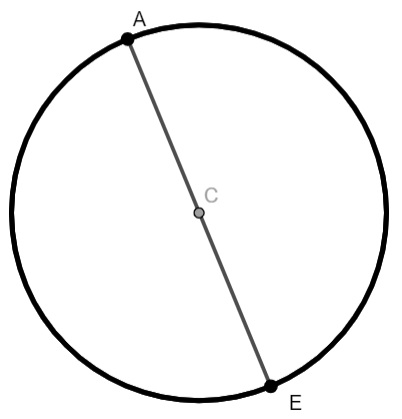
O comprimento AE é igual ao diâmetro da circunferência, para encontrar o raio, basta dividir por dois, ou seja, r = 7 cm.
C = 2 · 3,1 · 7
C = 6,2 · 7
C = 43,4 cm
Acesse também: As principais diferenças entre as figuras planas e as figuras espaciais
Área da circunferência
Assim como o comprimento, para encontrar a área da circunferência, basta utilizarmos a seguinte fórmula:
A = π · r²
Exemplo:
Calcule a área de uma circunferência que possui raio igual a 4 cm (use π = 3).
A = π · r²
A= 3 · 4²
A= 3 · 16
A = 48 cm²
Equação reduzida da circunferência
Na geometria analítica, é bastante comum procurar equações que representem as figuras planas. A circunferência é uma dessas figuras e possui sua equação reduzida e geral. A equação reduzida de uma circunferência de raio r e centro C (xc, yc) é representada por:
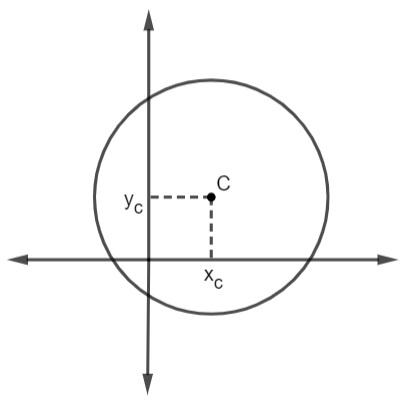
(x – xc)² + (y – yc)² = r
Equação geral da circunferência
A equação geral da circunferência é encontrada com base no desenvolvimento da equação reduzida. Ao resolver os produtos notáveis, encontraremos a seguinte equação:
x² + y² – 2xcx – 2yby + (xc² + yc² – r²) = 0
Exemplo:
Dada a circunferência, encontre a sua equação geral e a sua equação reduzida.
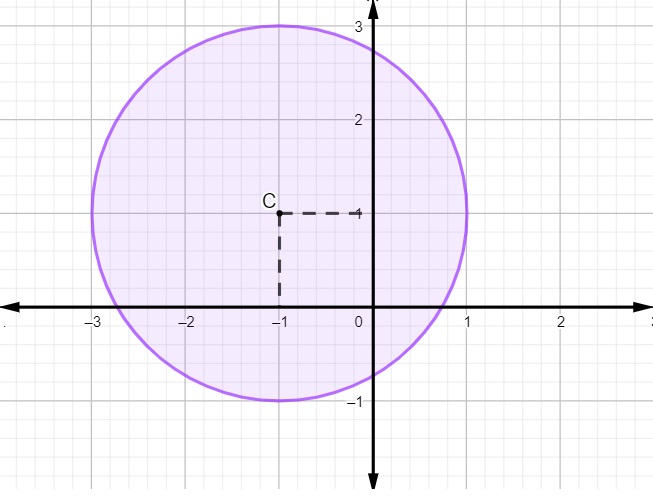
Primeiro encontraremos a equação reduzida, para isso, vamos encontrar o centro e o raio. Note que o centro da circunferência é o ponto C (-1,1). Para encontrar o raio, basta perceber que a extremidade da circunferência fica a duas unidades do centro, sendo assim, o raio é igual 2. Então, temos a sua equação reduzida.
Equação reduzida:
(x – (-1))² + (y – 1)² = 2
(x + 1)² + (y – 1)² = 2
Equação geral:
Para encontrar a equação geral, vamos desenvolver os produtos notáveis, encontrando a seguinte equação:
x² + 2x + 1 + y² – 2y + 1 = 2
x² + y² + 2x – 2y + 2 – 2 = 0
x² + y² + 2x – 2y = 0
Exercícios resolvidos
Questão 1 – (IFG 2019) Se o raio R de uma circunferência for reduzido pela metade, é correto afirmar que:
A) O valor da área círculo ficará reduzido pela metade do valor da área do círculo inicial de raio R.
B) O valor da área do círculo ficará a ¾ do valor da área do círculo inicial de raio R.
C) O comprimento da circunferência se reduzirá a ¼ do valor do comprimento da circunferência inicial de raio R.
D) O comprimento da circunferência se reduzirá à metade do valor do comprimento da circunferência inicial de raio R.
Resolução
Alternativa D
Se o raio for a metade, então ele será R/2. Analisando as alternativas, vamos verificar a redução na área e no comprimento:
Sabemos que a área é A = π r², se o raio for reduzido pela metade, teremos:
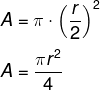
Assim, o raio será ¼ do raio anterior, o que faz com que as alternativas “a” e “b” sejam falsas.
Calculando o comprimento, temos que:
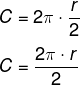
Note que o comprimento reduziu-se pela metade, o que faz com que a alternativa “d” seja a correta.
Questão 2 – Um ciclista completou 20 voltas em uma praça que possui 14 metros de raio e formato circular. Utilizando π = 3,14, podemos afirmar que ele percorreu aproximadamente:
A) 3 km
B) 3,5 km
C) 3,8 km
D) 4 km
E) 4,2 km
Resolução
Alternativa B
Primeiro calcularemos o comprimento de uma volta:
C = 2 · π · r
C = 2 · 3,14 · 14
C = 6,28 · 14
C = 87,92 m
Agora multiplicaremos pelo número de voltas.
87,92 · 40 = 3.516,8
Aproximadamente, 3,5 km.