Círculos

Um círculo é o conjunto de pontos em que, dados um ponto central O e uma distância r, a distância entre um ponto e o ponto central O deve ser menor ou igual a r.

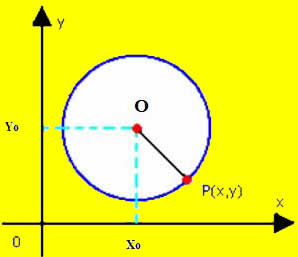
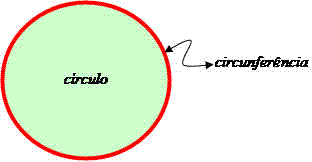
Em outras palavras, um círculo é uma região plana que apresenta uma circunferência como limite, como mostra a figura a seguir:

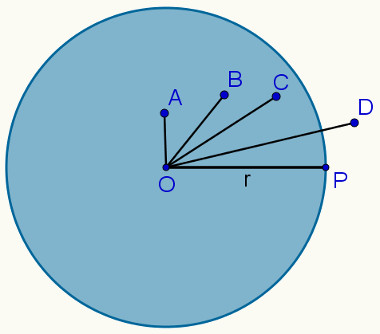
No círculo acima, foram destacados alguns pontos pertencentes a ele e um ponto que está fora dele. Para perceber quais desses pontos pertencem ao círculo, basta determinar quais deles possuem distância menor que r, que é distância entre a borda do círculo e o seu ponto central.

Assim, a distância entre dois pontos é o comprimento do segmento de reta que os liga. Quando esse segmento atravessa a borda do círculo, o ponto em sua extremidade fica de fora dessa figura. Caso isso não aconteça, o ponto é pertencente ao círculo. No exemplo acima, os pontos do círculo são: o próprio O, P, A, B, e C. O único ponto que não pertence a ele é D.

Tópicos deste artigo

• 1 - Elementos do círculo

Elementos do círculo

→ Raio

É a distância entre o centro e a borda de um círculo. Nessa definição, é a medida de r e é comumente representado por essa letra.

→ Diâmetro

É o segmento de reta que liga dois pontos pertencentes à borda de um círculo e que passa pelo seu centro. Dessa maneira, o diâmetro sempre terá o dobro da medida do raio.

→ Comprimento

O comprimento de um círculo, também chamado perímetro, é igual ao comprimento da circunferência que o limita e pode ser obtido pela seguinte expressão:

C = 2·π·r

A partir do comprimento do raio de um círculo, é possível calcular seu comprimento, pois π tem valor fixo: aproximadamente igual a 3,14.

→ Área do círculo

A área do círculo é a quantidade de espaço que ele ocupa no plano e pode ser obtida usando a seguinte expressão:

A = π·r²

Assim, conhecendo o raio de um círculo, é possível encontrar sua área.

→ Setor circular

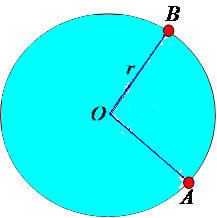
Setor circular é uma fatia do círculo determinado por dois de seus raios. Por exemplo: a parte clara da figura a seguir é um setor circular e a parte escura, outro.

Observe que o setor circular mais claro também foi destacado com um ângulo. A partir desse ângulo, é possível descobrir a área do setor circular (x). Para isso, basta usar a área total do círculo (A = π·r2) e o ângulo total do círculo (360º) na regra de três. Dessa maneira, temos:

π·r² = 360
x         α

360x = α·π·r²

x = α·π·r²
     360

Portanto, pode-se usar a regra de três ou a expressão acima para determinar a medida da área de um setor circular.

1º Exemplo – Calcule a área e o perímetro de um círculo cujo raio mede 25 centímetros.

Solução: Como o raio mede 25 cm, basta substituir esse valor na fórmula da área e do comprimento (que é o perímetro do círculo). Para esses cálculos, lembre-se de que π é, aproximadamente, igual a 3,14:

A = π·r²

A = 3,14·25²

A = 3,14·625

A = 1962,5 cm²

2º Exemplo – Calcule a área de um setor circular cujo ângulo central mede 90°.

Solução: Usamos a expressão obtida para x, que representa a área do setor circular.

x = α·π·r²
    360

x = 90·3,14·25²
     360

x = 3,14·625
    4

x = 1962,5
     4

x = 490,6 cm² aproximadamente.

Note que 90° é um quarto de 360°. Logo, a área do setor circular deve ser um quarto da área do círculo.

Aproveite para conferir nossa videoaula sobre o assunto: