O círculo trigonométrico é uma circunferência usada para relacionar números reais a medidas de ângulos. Cada ponto desse círculo, portanto, representa um ângulo por meio de um número real.
Construir um círculo trigonométrico é simples: basta usar o compasso para construir uma circunferência de raio 1, com o centro no ponto C = (0,0) do plano cartesiano, como mostra a imagem a seguir:
Ângulos no círculo trigonométrico
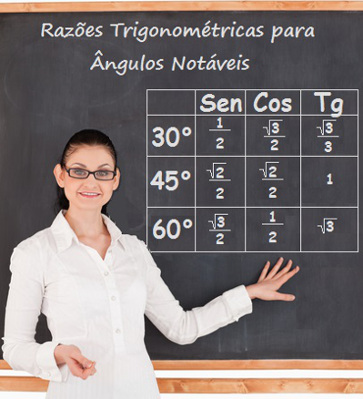
Os ângulos são construídos com o vértice no centro dessa circunferência e seus lados são os raios dela. Também fica definido que o sentido da abertura dos ângulos é o anti-horário, e o raio (em dourado) que aparece na figura acima é a base para esse sentido. Em outras palavras, todos os ângulos são representados com o primeiro lado sobre esse raio e o segundo determinando a abertura em sentido anti-horário. Os ângulos de 30°, 45° e 60° são representados da seguinte forma:
Relação entre ângulos e arcos
Como são ângulos centrais, eles possuem a mesma medida do arco relacionado. Esse arco, em termos de números reais, pode ser calculado por regra de três, e a correspondência é feita ligando a medida do comprimento do arco ao ângulo que ele representa.
Para isso, basta saber que o maior ângulo central encontrado em uma circunferência (nesse caso, no círculo trigonométrico) é de 360°, que corresponde a seu comprimento total (C), obtido da seguinte maneira:
C = 2·π·r
Como o raio do círculo trigonométrico deve ser 1, teremos:
C = 2·π·1
C = 2π
O comprimento total dos círculos trigonométricos é 2π. Assim, podemos dizer que 360° = 2π.
Números reais atribuídos a ângulos no círculo trigonométrico
Sabendo que 360° está relacionado a 2π por meio do círculo de raio 1, podemos relacionar qualquer outro ângulo a um número em função de π. Por exemplo, o ângulo de 180°:
360° = 2π
180° x
Resolvendo essa regra de três, teremos:
360x = 180·2·π
x = 360·π
360
x = π
O ângulo de 180° está relacionado ao número real π.
Usando exatamente o mesmo raciocínio, podemos encontrar as seguintes equivalências:
90° = π/2
60° = π/3
45° = π/4
30° = π/6

Círculo trigonométrico com ângulos notáveis
Razão seno e razão cosseno
No círculo trigonométrico, é possível encontrar as medidas de seno e cosseno. Observe na imagem a seguir o ângulo de 45°:
Observe que qualquer ângulo pode ser usado para construir um paralelogramo ABCD. Nesse caso, a imagem retrata o paralelogramo relativo ao ângulo de 45°. O comprimento do lado DC é sempre o cosseno do ângulo em questão e o comprimento do lado AD é sempre igual ao seno desse ângulo.
Essas medidas podem ser obtidas com alguns instrumentos que medem o comprimento com a precisão de quatro casas decimais ou mais, ou conforme a tabela a seguir que contém as medidas dos segmentos AD e DC para todos os ângulos de 0° a 90°:






.jpg)