Cilindro

 O cilindro é um sólido geométrico estudado na geometria espacial e classificado como corpo redondo, pois apresenta duas bases no formato de círculo.

Existem algumas classificações possíveis para os cilindros. Ele pode ser oblíquo, quando o eixo não é perpendicular à base; reto, quando a altura coincide com o eixo do cilindro; e, em um cilindro reto, quando o diâmetro da base coincide com a altura, esse cilindro é classificado também como equilátero. O cálculo da área total de um cilindro e de seu volume é feito com a utilização de fórmulas específicas.

Leia também: Principais diferenças entre figuras planas e espaciais

Tópicos deste artigo

• 1 - Classificação dos cilindros
• 2 - Planificação do cilindro
• 3 - Área do cilindro
• 4 - Volume do cilindro
• 5 - Secção no cilindros
• 6 - Exercícios resolvidos

Classificação dos cilindros

Existem duas possíveis classificações para o cilindro: reto ou oblíquo, o que depende do formato desse sólido.

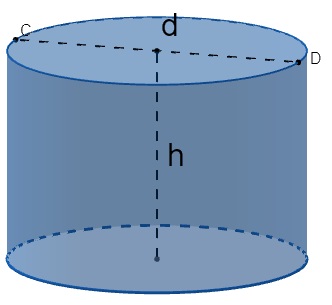
Dizemos que um cilindro é reto, quando o eixo do cilindro é perpendicular a sua base.

Existe um caso particular de cilindro reto: quando ele possui a altura igual ao diâmetro da sua base, dizemos que esse cilindro é equilátero.

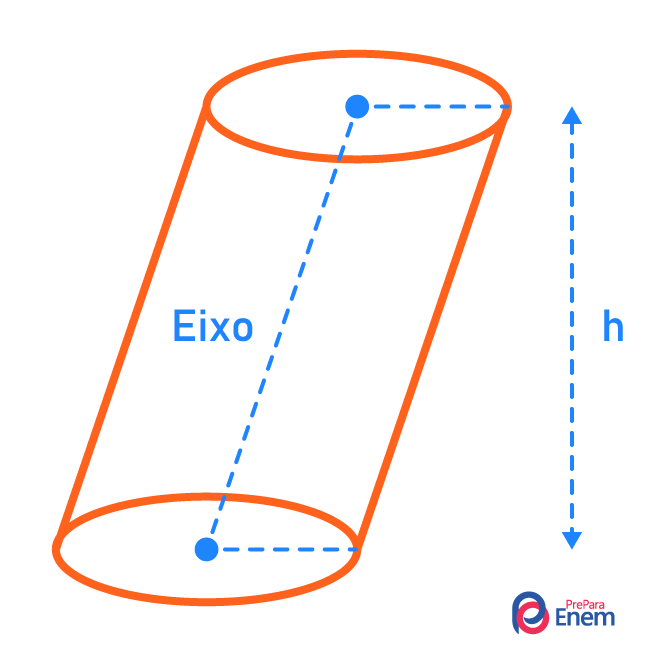
Dizemos que o cilindro é oblíquo quando o eixo do cilindro não é perpendicular a sua base. Nesse caso, é possível perceber que o cilindro é um pouco inclinado em relação à base.

Planificação do cilindro

A planificação do cilindro nada mais é do que a representação bidimensional das formas geométricas que formam esse sólido geométrico. Quando planificamos o cilindro, é possível perceber que ele é formado por dois círculos, que representam as suas bases, e um retângulo, que representa a sua área lateral, conforme a imagem a seguir:

Veja também: Planificação de sólidos geométricos – representação da superfície do poliedro no plano

Área do cilindro

Conhecemos como área total do cilindro a área da região que contorna o sólido. No cilindro, quando fazemos a sua planificação, é possível identificar duas áreas no formato de um círculo e uma área lateral no formato de um retângulo; sendo assim, a área total de um cilindro pode ser calculada por:

A_T = 2A_b + A_l

Como a base é um círculo, então a área da base é calculada por:

A_b = πr²

A área lateral é igual à área do retângulo. Esse retângulo possui altura igual a 2πr e base medindo h, então a área lateral é calculada por:

A_l = 2πrh

Sendo assim, a área total é calculada por:

A_T = 2A_b + A_l

A_T = 2πr² + 2πrh

A_T = 2πr( r + h)

Volume do cilindro

Para encontrar o valor do volume do cilindro, calculamos o produto entre a área da base e a altura desse sólido. Como a base é um círculo, então calculamos o volume com a seguinte fórmula:

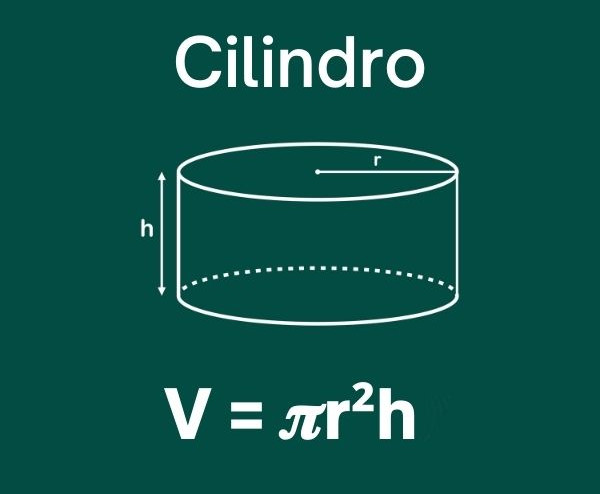
V = A_b · h

V = πr²h

Exemplo:

Dado o cilindro a seguir, calcule o valor da sua área total e de seu volume.

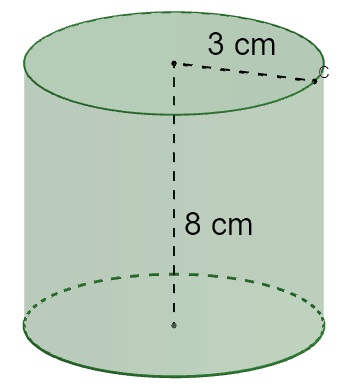
Sabemos que:

• raio r = 3 cm;

• altura h = 8 cm.

Então, vamos calcular a área total:

A_T = 2πr( r + h)

A_T = 2π · 3( 3 + 8)

A_T = 6π · 11

A_T = 66π

Agora calcularemos o volume:

V = πr²h

V = π · 3² · 8

V = π · 9 · 8

V = 72π

Leia também: Circunferência e círculo: definições e diferenças básicas

Secção no cilindros

Conhecemos como secção a região formada pela intersecção entre o cilindro e um plano. Existem dois tipos mais recorrentes de secção: a transversal e a meridiana.

• Secção transversal: uma secção do cilindro é conhecida como transversal quando ela é feita paralelamente ao eixo da base, dividindo o sólido em dois novos cilindros. Além disso, a intersecção do plano com o sólido forma um círculo, como na imagem a seguir:

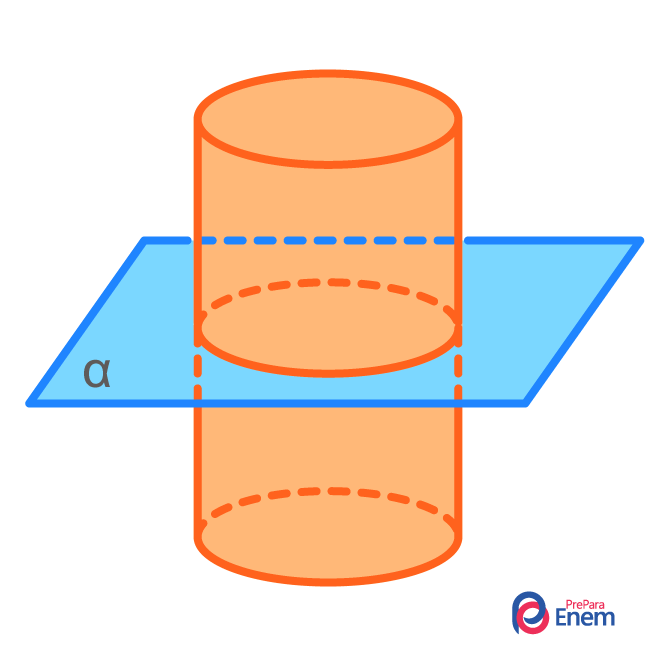
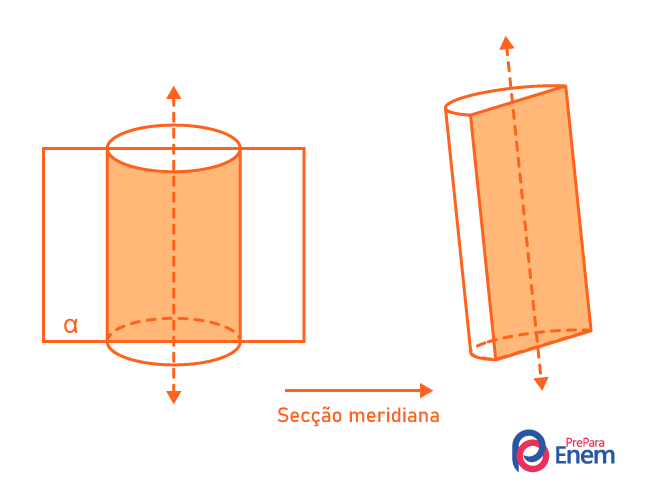
• Secção meridiana: sempre contém o eixo do cilindro, dividindo-o ao meio. A intersecção entre o cilindro e o plano formam um retângulo.

Exercícios resolvidos

Questão 1 – O volume de um cilindro é igual a 4.464 cm³ e o seu diâmetro mede 6 cm. Qual é a medida da altura desse cilindro? (Considere π = 3,1).

A) 100 cm.
B) 110 cm.
C) 120 cm.
D) 140 cm.
E) 160 cm.

Resolução

Alternativa E. Sabemos que V = πr²h. Além disso, temos:

• π = 3,1;

• r = 3 (o raio é metade do diâmetro);

• V = 4.464).

Assim, substituindo os valores conhecidos, temos que:

V = 3,1 · 3² · h

4.464 = 3,1 · 9 · h

4.464= 27,9h

h = 4.464 : 27,9

h = 160

Questão 2 – Em uma determinada fábrica, o preço do metro quadrado do vidro depende das características que ele possui. Será confeccionado um reservatório de vidro no formato cilíndrico com 1,5 m de raio e 2,5 m de altura. Sabendo que o vidro escolhido custa R$ 17,60 m², o valor gasto somente em vidro para confeccionar esse reservatório é:

(Use π = 3)

A) R$ 525,30.
B) R$ 554,80.
C) R$ 633,60.
D) R$ 875,20.
E) R$ 926,50.

Resolução

Alternativa C. Para descobrir a quantidade de vidro a ser utilizada, calcularemos a área total do cilindro.

A_T = 2πr( r + h)

A_T = 2 · 3 · 1,5( 1,5 + 2,5)

A_T = 2 · 3 · 1,5 · 4

A_T = 2 · 3 · 1,5 · 4

A_T = 36 m²

Sabendo que o m² é 17,60, então o valor gasto será:

36 · 17,60 = 633,60