Perímetro é a medida do contorno de uma figura plana, como polígonos e círculos. Lembre que um polígono é uma figura plana e fechada formada por segmentos que se encontram apenas nas extremidades. Para calcular o perímetro de um polígono, basta somar as medidas dos lados. Para calcular o perímetro de um círculo — que é o comprimento da circunferência correspondente —, utilizamos a expressão \(p=2πr\), em que r é o raio do círculo.
Leia também: Geometria plana no Enem — o que estudar
Tópicos deste artigo
- 1 - Resumo sobre perímetro
- 2 - O que é perímetro?
- 3 - Fórmulas do perímetro
- 4 - Qual a unidade de medida do perímetro?
- 5 - Como se calcula o perímetro?
- 6 - Qual a diferença entre perímetro e área?
- 7 - Qual a diferença entre perímetro e comprimento?
- 8 - Exercícios resolvidos sobre perímetro
Resumo sobre perímetro
-
A medida do contorno de uma figura plana é chamada de perímetro dessa figura.
-
O perímetro de um polígono é a soma de todos os lados.
-
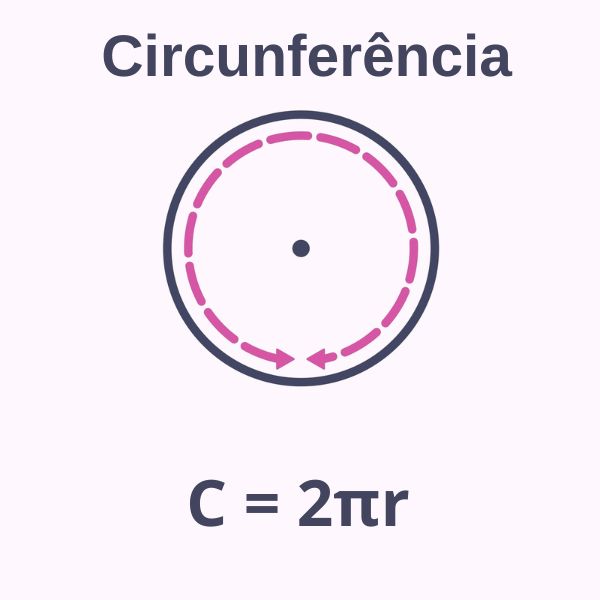
O perímetro de um círculo de raio r é o comprimento da circunferência de raio r, dado por:
\(C = 2πr\)
-
A área de uma figura plana é a medida da superfície.
O que é perímetro?
Perímetro é a medida do contorno de uma figura. No caso dos polígonos, em que o contorno é formado por segmentos de reta, o perímetro é a soma de todos os lados. Já no caso do círculo, em um o contorno é curvo, o perímetro é o comprimento da circunferência de mesmo raio. Se o raio do círculo é r, seu perímetro é dado por \(C = 2πr\).
Fórmulas do perímetro
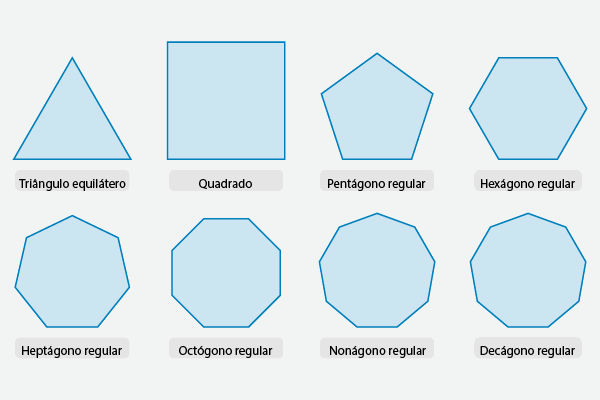
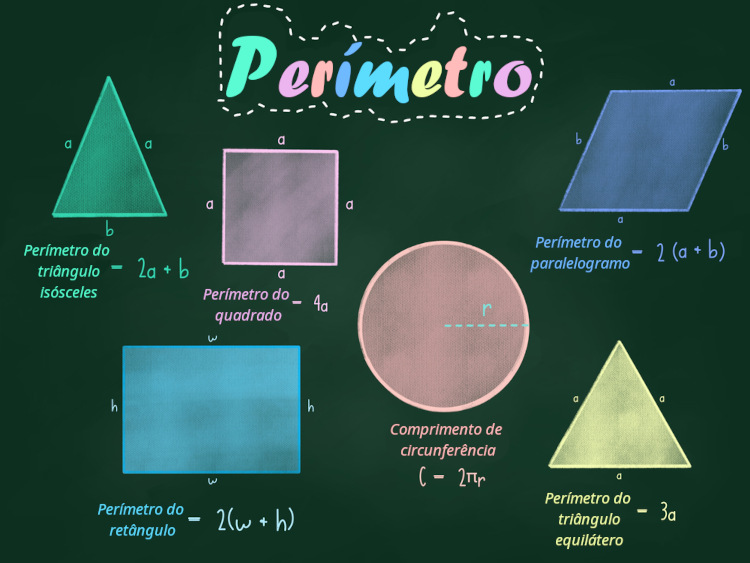
Observe a imagem abaixo, que apresenta algumas fórmulas para perímetros de polígonos e do círculo. Perceba que, no caso dos polígonos, não é necessário decorar essas expressões: basta conhecer a medida de cada lado para obter o perímetro.
Qual a unidade de medida do perímetro?
Nos polígonos, a unidade de medida do perímetro é a mesma unidade de medida dos lados. Por exemplo, se o lado de um quadrado mede 2 cm, então todos os quatro lados medem 2 cm. Assim, o perímetro é 2 cm + 2 cm + 2cm + 2 cm = 8 cm.
Já no cálculo do comprimento de uma circunferência, a unidade de medida utilizada é a mesma do raio, como veremos adiante no exemplo 2.
Veja também: Afinal, qual é a diferença entre círculo e circunferência?
Como se calcula o perímetro?
Vejamos dois exemplos de como calcular o perímetro de uma figura plana.
-
Exemplo 1: Qual o perímetro de um triângulo equilátero com 4 cm de lado?
Em um triângulo equilátero, os três lados possuem a mesma medida. Assim, o perímetro de um triângulo equilátero é 12 cm, pois 4 cm + 4 cm + 4cm = 12 cm.
-
Exemplo 2: Qual o perímetro de um círculo com 3 cm de raio?
O perímetro de um círculo com 3 cm de raio é o comprimento da circunferência com 3 cm de raio:
\(C = 2 πr\)
\(C = 2⋅π ⋅3 cm\)
\(C = 6π\ cm\)
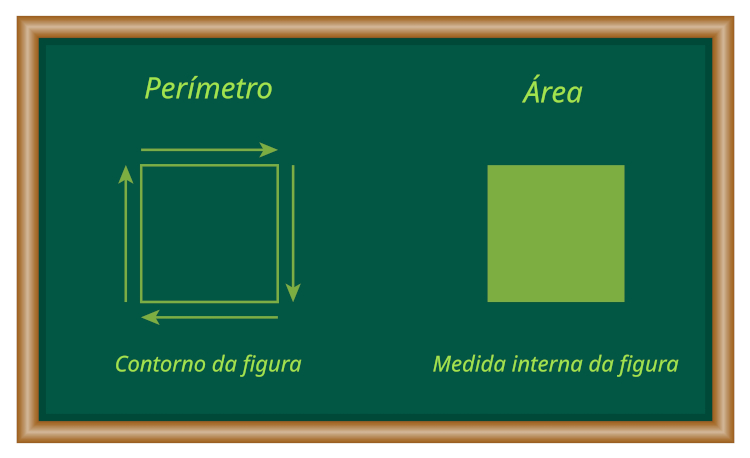
Qual a diferença entre perímetro e área?
Enquanto o perímetro é a medida do contorno de uma figura plana, a área é a medida de sua superfície, ou seja, da região interna.
Qual a diferença entre perímetro e comprimento?
A palavra comprimento normalmente se refere à medida de um segmento, ou seja, à distância entre dois pontos. Em um retângulo, por exemplo, é comum chamar o lado maior de comprimento e o lado menor de largura. Assim, em um polígono, o perímetro é a soma dos comprimentos dos lados.
Saiba mais: Como calcular a área de figuras planas
Exercícios resolvidos sobre perímetro
Questão 1
Se o perímetro de um pentágono regular é 30 cm, então a medida de cada lado é igual a
a) 5 cm.
b) 6 cm.
c) 7 cm.
d) 8 cm.
e) 9 cm.
Resolução
Seja l a medida em cm do lado do pentágono regular. Como esse polígono possui 5 lados de mesma medida, temos que:
\(5 ⋅l = 30\ cm\)
\(l=\frac{30}5\ cm\)
\(l=6\ cm\)
Alternativa B.
Questão 2
Em um retângulo, o lado maior mede 20 cm. Qual a medida do lado menor, sabendo que o perímetro é 72 cm?
a) 12 cm
b) 13 cm
c) 14 cm
d) 15 cm
e) 16 cm
Resolução
Seja b a medida em cm do lado menor do retângulo. Como os lados opostos de um retângulo são congruentes (têm a mesma medida), segue que:
20 + 20 + b + b = 72
40 + 2b = 72
2b = 32
b = 16 cm
Alternativa E.
Fontes
LIMA, E. L. Geometria Analítica e Álgebra Linear. Rio de Janeiro: IMPA, 2014.
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.