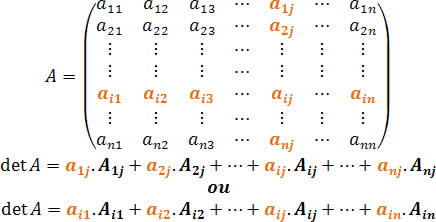No cálculo de determinantes, temos diversas regras que auxiliam na realização desses cálculos, contudo nem todas essas regras podem ser aplicadas a qualquer matriz. Diante disso, temos o Teorema de Laplace, que pode ser aplicado a qualquer matriz quadrada.
Um fato indiscutível é quanto à aplicação da regra de Sarrus para matrizes quadradas de ordem 2 e 3, sendo essa a mais indicada para a realização dos cálculos do determinante. Contudo, a regra de Sarrus não é aplicável para as matrizes de ordens superiores a 3, restando-nos apenas a regra de Chió e o Teorema de Laplace para a solução desses determinantes.
Quando falamos sobre o Teorema de Laplace automaticamente devemos relacioná-lo ao cálculo do cofator, pois esse é um elemento essencial para encontrarmos o determinante de uma matriz através desse teorema.
Diante disso, surge a grande questão: quando usar o Teorema de Laplace? Por que usar esse teorema e não a regra de Chió?
No Teorema de Laplace, como você pode ver no artigo relacionado abaixo, esse teorema realiza diversos cálculos de determinante de “sub-matrizes” (matriz de ordem menor obtidas com elementos de uma matriz principal), fazendo com que seja um trabalho mais complexo do que seria com a regra de Chió. Façamos uma análise na expressão do Teorema de Laplace, pois assim iremos notar algo interessante que nos auxiliará a responder este questionamento.
A matriz A é uma matriz quadrada de ordem 4.

Pelo Teorema de Laplace, se escolhermos a primeira coluna para serem calculados os cofatores, teremos:
detA=a11.A11+a21.A21+a31.A31+a41.A41
Note que os cofatores (Aij) são multiplicados pelos seus respectivos elementos da matriz A4x4, como ficaria esse determinante se os elementos: a11,a31,a41 forem iguais a zero?
detA=0.A11+a21.A21+0.A31+0.A41
Veja que não há motivo para calcularmos os cofatores A11, A31 e A41, pois eles estão multiplicados por zero, ou seja, o resultado dessa multiplicação será zero. Assim, para o cálculo desse determinante, restarão o elemento a21 e o seu cofator A21.
Portanto, sempre quando tivermos matrizes quadradas, nas quais uma de suas filas (linha ou coluna) tiverem vários elementos nulos (iguais a zero), o Teorema de Laplace se torna a melhor escolha para o cálculo do determinante.
Videoaulas relacionadas: