Entre as relações métricas que temos no triângulo, algumas merecem destaque por causa das propriedades especiais que possuem. Por ora falaremos das bissetrizes e do incentro em um triângulo qualquer.
Portanto, devemos compreender a definição da bissetriz de um ângulo e aplicá-la em um triângulo.
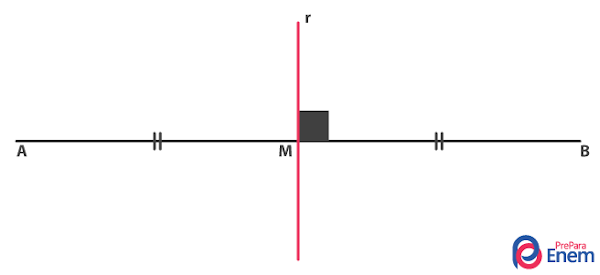
A bissetriz é a reta (semirreta, segmento de reta) que sai do vértice de um ângulo, dividindo este ângulo em dois ângulos iguais. Por exemplo, a bissetriz do ângulo de 90° é o segmento que divide este ângulo em dois ângulos iguais a 45°. Até então, tudo isso não passa de uma breve revisão. Vamos agora conhecer as propriedades dessas retas bissetrizes no triângulo.
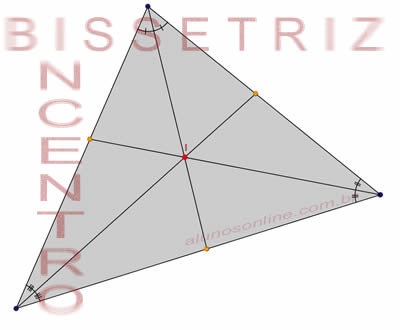
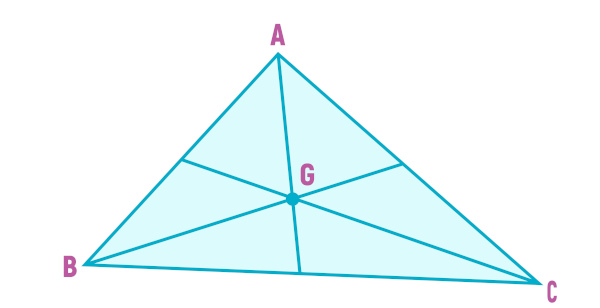
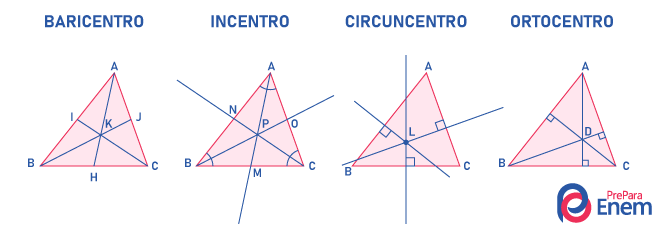
No triângulo temos três vértices, portanto teremos três ângulos internos. Em cada um desses ângulos internos podemos traçar uma reta, partindo do vértice que secciona o ângulo ao meio, ou seja, podemos traçar uma bissetriz. Ao traçarmos as três bissetrizes de um triângulo, elas vão se intersectar em um único ponto, sendo este ponto denominado incentro.

Entretanto, existe um motivo em especial para que esse encontro das bissetrizes se chame incentro: este ponto recebe tal denominação porque é o centro da circunferência inscrita no triângulo. Veja a imagem a seguir:

Note que a circunferência está completamente dentro do triângulo, por isso ela é uma circunferência inscrita no triângulo, no qual toca cada lado do triângulo em um único ponto.