Baricentro de um triângulo é o ponto de encontro das três medianas do triângulo. Geralmente, é representado pela letra G. Para encontrar o baricentro, é necessário traçar as três medianas do triângulo e, assim, localizar o ponto de encontro entre elas.

O baricentro é um dos pontos notáveis do triângulo e possui propriedades importantes. Para encontrar o baricentro quando estudamos o triângulo representado em um plano cartesiano, calculamos a média aritmética entre as coordenadas dos vértices do triângulo.

Leia também: Propriedades do triângulo isósceles e do equilátero

Tópicos deste artigo

• 1 - Resumo sobre baricentro do triângulo
• 2 - O que é o baricentro?
• 3 - Propriedades do baricentro
• 4 - Como calcular o baricentro

Resumo sobre baricentro do triângulo

• O baricentro é um ponto notável do triângulo.

• É o ponto de encontro das três medianas do triângulo, geralmente representado por G.

• Para calcular as coordenadas do baricentro do triângulo A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C), utilizamos a fórmula:

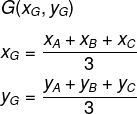
O que é o baricentro?

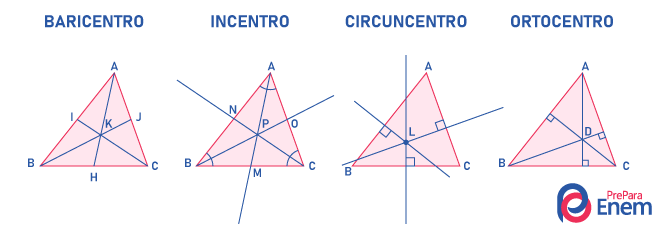
O triângulo é o sólido geométrico mais simples de todos, mas que é estudado a fundo na geometria. A partir do estudo do triângulo, foram encontrados quatro pontos notáveis, sendo um deles o baricentro. Os demais são denominados incentro, circuncentro e ortocentro.

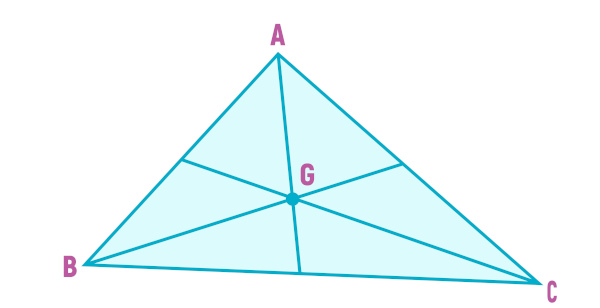
O baricentro, em específico, é o ponto de encontro das três medianas do triângulo. Portanto, para encontrar o lugar geométrico que o baricentro ocupa, traçamos as três medianas do triângulo e marcamos o ponto de encontro entre elas, que é comumente representado pelo ponto G. Vejamos a seguir a representação do baricentro de um triângulo.

A mediana é o segmento de reta que vai do ponto médio de um lado do triângulo até o vértice oposto a esse lado. Traçaremos as medianas do triângulo ABC, começando pela mediana em relação ao vértice A:

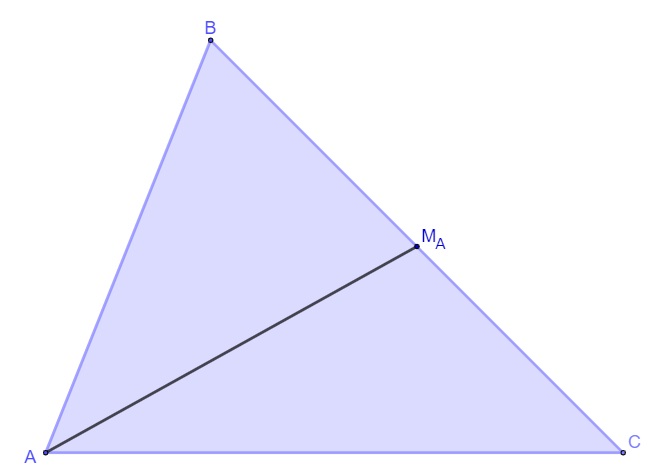
Agora, traçaremos mais uma mediana, a relativa ao vértice B:

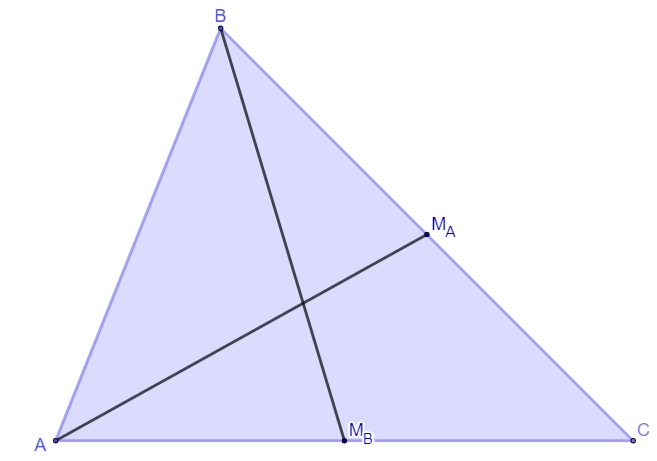
Por último, vamos traçar a mediana relativa ao vértice C e encontrar o baricentro.

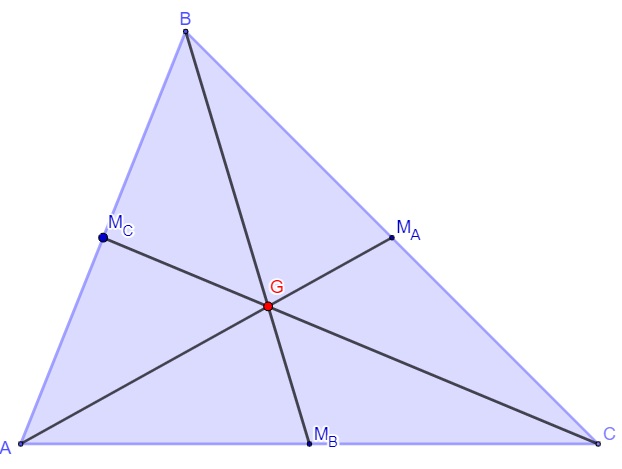
Dessa forma, demarca-se o baricentro desse triângulo, representado por G.

Leia também: Condição de existência de um triângulo

Propriedades do baricentro

O baricentro possui duas propriedades importantes. Vejamos cada uma delas a seguir.

• 1ª propriedade: o baricentro é um ponto interno do triângulo.

Ao traçar as medianas, o segmento de reta sempre estará na parte interna do triângulo, como consequência de sua definição, pois a mediana liga o vértice ao ponto médio. Sendo assim, o baricentro sempre será um ponto interno, independentemente do formato do triângulo.

• 2ª propriedade: o baricentro divide qualquer uma das medianas em dois segmentos, sendo que o comprimento destes estão em uma razão de 1 para 2.

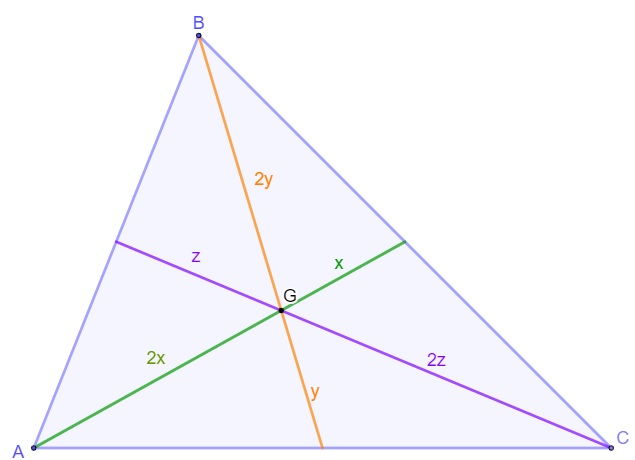
Como calcular o baricentro

A partir dos estudos da geometria analítica, foi possível realizar a representação de um triângulo no plano cartesiano. Com a representação do triângulo, conhecendo as coordenadas de seus vértices, é possível calcular as coordenadas do baricentro do triângulo.

Dado um triângulo cujos vértices são os pontos A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C), com baricentro possuindo coordenadas G(x_G, y_G), basta calcularmos a média aritmética dos valores de x e y para encontrar as coordenadas do baricentro desse polígono.

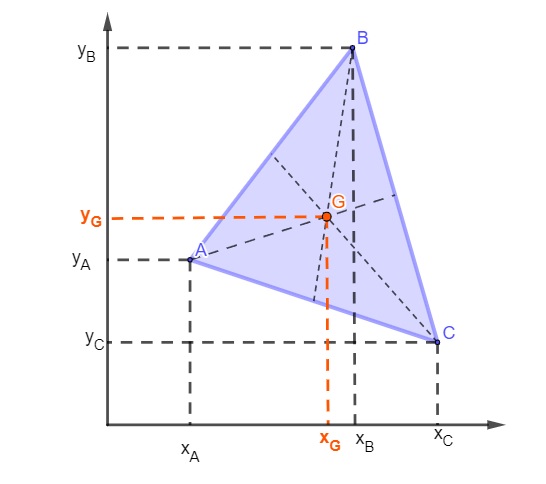
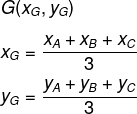
Exemplo:

Um triângulo possui vértices localizados nos pontos A(2, 3), B(5, – 4) e C(– 1, – 2). Qual são as coordenadas de seu baricentro?

Resolução:

Para encontrar suas coordenadas, começaremos por x_G.

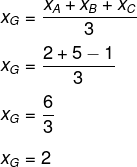
Agora, encontraremos y_G:

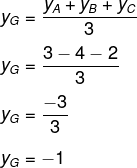
Portanto, o baricentro desse triângulo é o ponto G(2, – 1).

Leia também: Bissetriz e incentro de um triângulo

Exercícios resolvidos sobre baricentro de um triângulo

Questão 1

Um triângulo possui baricentro com as coordenadas G(– 1, 2). Sabendo que as coordenadas dos vértices A, B e C são, respectivamente, (4, 2), (– 2, 3) e (x, y), a diferença de y – x é igual a

A) 3.

B) 4.

C) 5.

D) 6.

E) 7.

Resolução:

Alternativa D

Sabemos que:

x_A = 4

x_B = – 2

x_G = – 1

Então, calcula-se o seguinte:

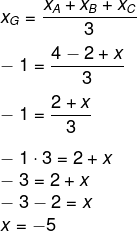
Além disso, sabemos que:

y_A = 3

y_B = – 4

y_G = 2

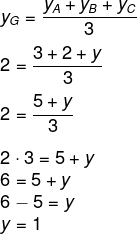
Agora, basta calcular a diferença entre y e x:

y – x = 1 – (– 5) = 1 + 5 = 6

Questão 2

Marque a alternativa que descreve de forma correta o que é o baricentro.

A) O baricentro é um segmento de reta notável do triângulo, formado pelo encontro das medianas.

B) O baricentro é um ponto notável do triângulo, formado pelo encontro das alturas.

C) O baricentro é um ponto notável do triângulo, formado pelo encontro das bissetrizes.

D) O baricentro é um ponto notável do triângulo, formado pelo encontro das medianas.

E) O baricentro é um segmento de reta notável do triângulo, formado pelo encontro das mediatrizes.

Resolução:

Alternativa D

O baricentro é o encontro das medianas de um triângulo.