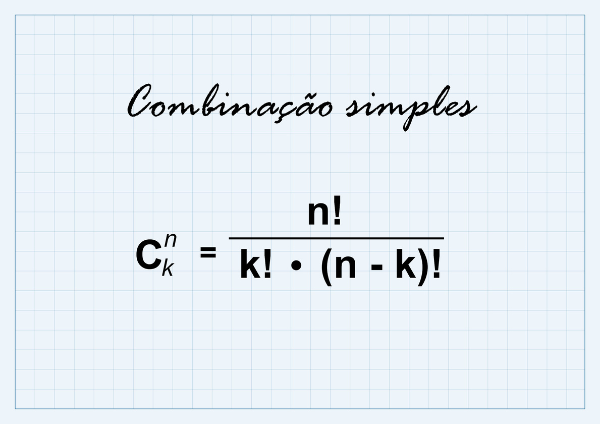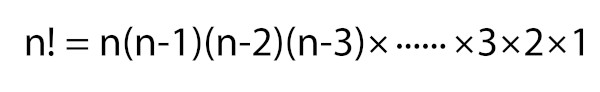Arranjo com repetição, ou arranjo completo, são todos os agrupamentos ordenados que podem ser formados com p elementos de um conjunto com n elementos, sendo que um mesmo elemento pode se repetir entre os p elementos.
O arranjo com repetição é um entre os vários tipos de agrupamentos estudados na análise combinatória, área da matemática que desenvolve técnicas para realizar contagens e encontrar o número de agrupamentos possíveis em determinadas situações, como a criação de senhas, de número de série de um produto, de placas veiculares, entre outras aplicações.
Para calcular o arranjo com repetição (AR) de n elementos tomados de p em p, utilizamos a fórmula:
ARn,p = np
Leia também: Análise combinatória no Enem — como esse tema é cobrado?
Tópicos deste artigo
- 1 - Resumo sobre arranjo com repetição
- 2 - O que é um arranjo com repetição?
- 3 - Qual a fórmula do arranjo com repetição?
- 4 - Como calcular o número de arranjos com repetição
- 5 - Exercícios resolvidos sobre arranjo com repetição
Resumo sobre arranjo com repetição
-
O arranjo com repetição é um tipo de agrupamento da análise combinatória.
-
O arranjo com repetição são os agrupamentos ordenados com p elementos entre n elementos de um conjunto, permitindo repetições.
-
Para calcular o arranjo com repetição, utilizamos a fórmula ARn,k = nk.
O que é um arranjo com repetição?
Conhecemos como arranjo com repetição todos os agrupamentos ordenados que podemos formar com p elementos entre os n elementos do conjunto.
Exemplo:
Quais agrupamentos ordenados podemos formar com duas letras entre as letras A, B, C, admitindo repetição?
Resolução:
Nesse caso, temos um arranjo com repetição, então, os casos possíveis são:
(A, A); (B, B); (C, C); (A, B); (B, A); (A, C); (C, A); (B, C); (C, B).
Dessa forma, há 9 arranjos com repetição possíveis.
Qual a fórmula do arranjo com repetição?
Em problemas envolvendo análise combinatória, é bastante comum que o interesse seja calcular a quantidade de agrupamentos possíveis em vez de listá-los, como foi feito no exemplo anterior. Para calcular de forma direta, a quantidade de arranjos com repetição que podemos fazer escolhendo p elementos de um conjunto com n elementos é dada por:
|
ARn,p = np |
-
AR → arranjo com repetição ou arranjo completo;
-
n → quantidade de elementos no conjunto;
-
p → quantidade de elementos que serão escolhidos.
Leia também: Como calcular permutações com repetição?
Como calcular o número de arranjos com repetição
Vejamos, a seguir, como aplicar a fórmula para encontrar a quantidade de arranjos com repetição que podemos formar em determinadas situações.
Exemplo:
Em um banco, a senha do cartão é composta por 4 números, que podem ser repetidos ou não, então, qual é a quantidade de senhas possíveis para esse cartão?
Resolução:
Sabemos que a senha é uma sequência de 4 algarismos e que a ordem é importante, logo, esse problema se trata de um arranjo com repetição.
Existem 10 algarismos de 0 até 9, então, n = 10, e serão escolhidos 4 deles, então, p = 4. Dessa forma, temos que:
AR10,4 = 104 = 10.000
Então, há 10 mil senhas distintas possíveis.
Leia também: Como é calculada a combinação com repetição?
Exercícios resolvidos sobre arranjo com repetição
Questão 1
As novas placas de automóveis do Mercosul são compostas por 4 letras, todas maiúsculas, e 3 algarismos, então, o número de placas possíveis nesse sistema pode ser calculado por:
A) 263
B) 104
C) 264 · 10
D) 10³ · 264
E) 104 · 263
Resolução:
Alternativa D
Estamos diante de dois arranjos com repetições, pois temos que escolher as 4 letras e também os 3 algarismos. Vale lembrar que placas admitem repetição e que a ordem é importante, então, para calcular o número de letras, temos que:
AR26,4 = 264
Para calcular os algarismos:
AR10,3 = 103
Assim, o número de arranjos possíveis é calculado pelo produto entre os dois arranjos com repetição:
103 · 264
Questão 2
Qual é a quantidade de números distintos, compostos por exatamente 3 algarismos, que podemos formar com os números 1, 2, 3, 4, 5?
A) 15
B) 27
C) 60
D) 75
E) 125
Resolução:
Alternativa E
A quantidade de números que podemos formar pode ser calculada por um arranjo com repetição, pois a ordem é importante e também podemos repetir os algarismos.
Então, temos que: n = 5 e p = 3.
AR5,3 = 53 = 125