Área do triângulo

A área de um triângulo pode ser obtida pela seguinte fórmula:

A = b·h
      2

A representa a área do triângulo; b, sua base; e h, sua altura. A unidade de medida de área deve ser elevada ao quadrado para indicar que se refere à área, e não ao comprimento.

Para garantir que a fórmula dada realmente é válida para calcular a área de um triângulo, devemos conhecer a área do paralelogramo:

A = b·h

Nessa fórmula, b é a base do paralelogramo e h é sua altura. Vejamos agora como é possível obter um paralelogramo a partir de um triângulo.

• Em um triângulo qualquer ABC, escolha os lados AB e BC e trace retas paralelas a eles passando pelos vértices A e C, como foi feito na figura a seguir:

• Seja D o ponto de encontro entre as retas paralelas traçadas, construa os segmentos AD e CD, que são paralelos a BC e AB, respectivamente. A figura ABCD é um paralelogramo, pois é um quadrilátero cujos lados opostos são paralelos.

• Uma das propriedades dos paralelogramos é a seguinte: lados opostos são congruentes. Assim sendo, as medidas dos lados AD e CD são iguais às medidas dos lados BC e AB, respectivamente. Como o lado AC do triângulo ABC é comum ao lado AC do triângulo ACD, podemos dizer que os triângulos ABC e ACD são congruentes.

  Não pare agora... Tem mais depois da publicidade ;)

• Como os dois triângulos são congruentes, suas áreas são iguais. Isso significa que metade da área do paralelogramo é igual à área de um dos triângulos. Para calcular a área do triângulo, apenas calculamos a área do paralelogramo de mesma base e altura e dividimos o resultado por 2.

A = b·h
      2

Exemplos

1º) Calcule a área de um triângulo cuja base mede 30 cm e a altura mede 40 cm.

A = b·h
      2

A = 30·40
      2

A = 1200
      2

A = 600 cm²

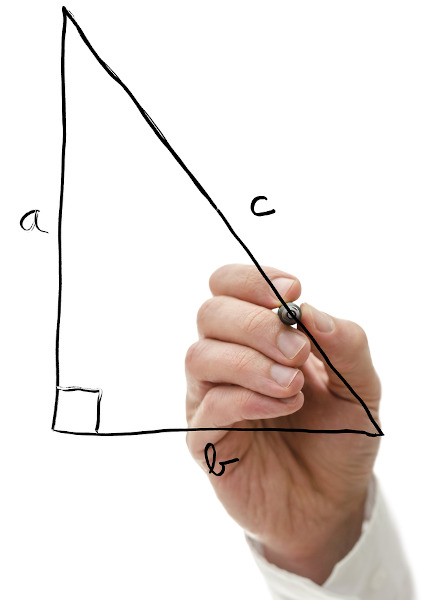
2º) Um lote de esquina tem formato de triângulo retângulo. Seu dono resolveu colocar grama em toda a superfície desse triângulo. Sabendo que o metro quadrado de grama custa R$ 18,00 e que os catetos desse triângulo medem 12 metros, calcule quanto essa pessoa gastará.

Solução:

Primeiramente, devemos descobrir a área do lote. Para tanto, observe que, em um triângulo retângulo, existe um ângulo de 90°. Essa é a condição para existir uma altura. Assim, um dos catetos é a base do triângulo e o outro é a altura. Sua área, portanto, será:

A = b·h
      2

A = 12·12
      2

A = 144
       2

A = 72 m²

Agora basta multiplicar esse resultado pelo valor da grama.

72·18 = 1296

Serão gastos R$ 1296,00.