A área do quadrado é a medida da sua superfície, ou seja, da região que essa figura ocupa. Para calcular a área do quadrado, é necessário saber a medida de seus lados, pois a área é calculada pelo produto entre as medidas da base e da altura do quadrado. Como os quatro lados do quadrado têm o mesmo tamanho, calcular sua área é o mesmo que elevar a medida de um de seus lados ao quadrado.
Leia também: Fórmulas para cálculo das áreas de figuras planas
Tópicos deste artigo
- 1 - Resumo sobre a área do quadrado
- 2 - Fórmula da área do quadrado
- 3 - Como se calcula a área do quadrado?
- 4 - Diagonal do quadrado
- 5 - Diferenças entre área do quadrado e perímetro do quadrado
- 6 - Exercícios resolvidos sobre a área do quadrado
Resumo sobre a área do quadrado
- O quadrado é um quadrilátero cujos lados possuem a mesma medida.
- A área do quadrado representa a medida de sua superfície.
- A fórmula da área do quadrado de lado l é: \(A=l^2\).
- A diagonal de um quadrado de lado l é dada por: \(d=l\sqrt2\) .
- O perímetro do quadrado é a medida do contorno da figura.
- O perímetro de um quadrado de lado l é dado por: \(P=4l\).
Fórmula da área do quadrado
Existe uma fórmula que determina a área de qualquer quadrado desde que se saiba o valor da medida de um de seus lados. Para chegarmos a ela, primeiro vejamos alguns casos específicos de área de quadrados.
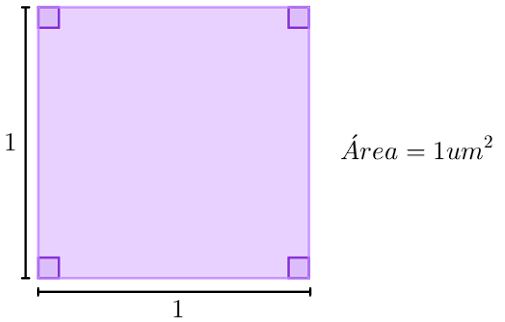
Há uma convenção matemática que determina o seguinte: um quadrado com uma unidade de medida de lado (chamado de quadrado unitário) possui uma área de 1 u.m.2 (1 unidade de medida ao quadrado).
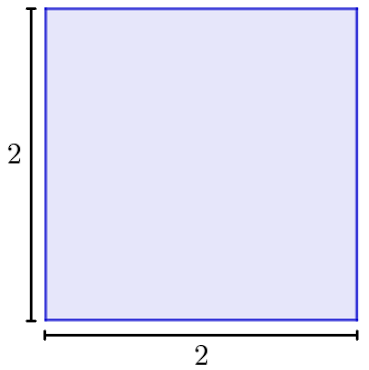
Com base nessa ideia, é possível expandi-la de forma a calcular a área de outros quadrados. Por exemplo, imagine um quadrado cujo lado mede 2 unidades de medida:
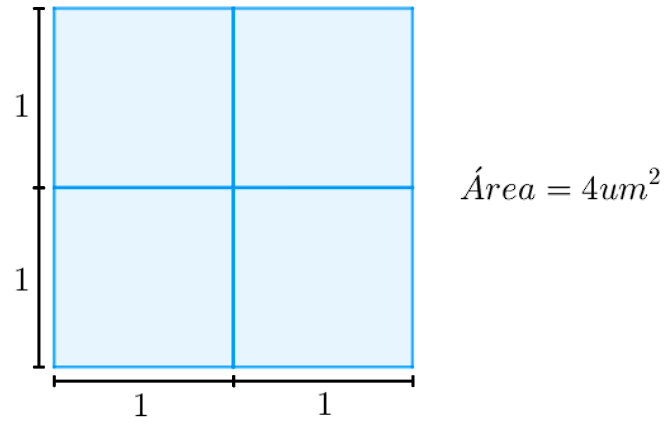
Para descobrir a medida da sua área, podemos dividir a medida dos seus lados até obtermos pequenas medidas de 1 unidade:
Assim, é possível ver que o quadrado de lados medindo 2 unidades pode ser dividido exatamente em 4 quadrados unitários. Portanto, como cada quadrado menor possui 1 u.m.2 de área, a área do quadrado maior mede \(4\cdot1\ u.m.^2=4\ u.m.^2\).
Se seguirmos esse raciocínio, um quadrado cujo lado mede 3 unidades de medida poderia ser dividido em 9 quadrados unitários e, portanto, teria uma área equivalente a 9 u.m.2, e assim por diante. Perceba que, nesses casos, a área do quadrado corresponde ao quadrado da medida do lado:
Lado medindo 1 unidade → Área = \(1\cdot1=1\ u.m.^2\)
Lado medindo 2 unidades → Área = \(2\cdot2=4\ u.m.^2\)
Lado medindo 3 unidades → Área = \(3\cdot3=9\ u.m.^2\)
No entanto, essa ideia não funciona apenas para números inteiros positivos mas também para qualquer número real positivo, ou seja, se um quadrado possui um lado medindo l, sua área é dada pela fórmula:
Área do quadrado= \(l.l=l^2\)
Como se calcula a área do quadrado?
Como visto, a fórmula da área do quadrado relaciona a área dessa figura com o quadrado da medida de seu lado. Assim, basta tomar a medida do lado do quadrado e elevar esse valor ao quadrado para a medida de sua área seja obtida.
Contudo, é possível calcular o inverso também, ou seja, com base no valor da área de um quadrado, pode-se calcular a medida de seus lados.
- Exemplo 1: Sabendo que o lado de um quadrado mede 5 centímetros, calcule a área dessa figura.
Substituindo l=5 cm na fórmula da área do quadrado:
\(A=l^2={(5\ cm)}^2=25\ cm^2\)
- Exemplo 2: Se a área de um quadrado é de 100 m2 , determine a medida do lado desse quadrado.
Substituindo A=100 m2 na fórmula da área do quadrado:
\(A=l^2\)
\(100\ m^2=l^2\)
\(\sqrt{100\ m^2}=l\)
\(l=10\ m\)
Leia também: Como calcular a área do triângulo?
Diagonal do quadrado
A diagonal de um quadrado é o segmento que une dois de seus vértices não adjacentes. No quadrado ABCD abaixo, a diagonal em destaque é o segmento AC, porém esse quadrado também possui outra diagonal, representada pelo segmento BD.
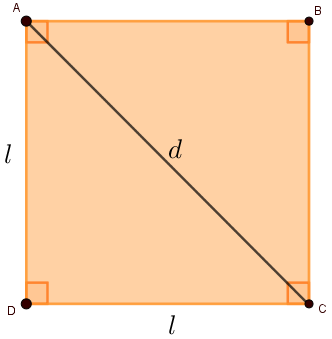
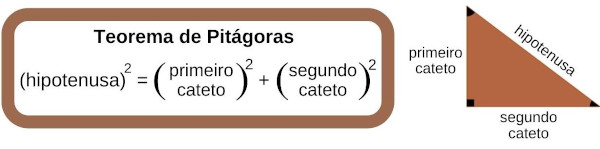
Perceba que o triângulo ADC é um triângulo retângulo, cujos catetos medem l e a hipotenusa mede d. Assim, pelo teorema de Pitágoras, é possível relacionar a diagonal de um quadrado com a medida de seus lados da seguinte forma:
\((Hipotenusa)^2=(cateto\ 1)\ ^2+(cateto\ 2)^2\)
\(d^2=l\ ^2+l^2\)
\(d^2=2l^2\)
\(d=l\sqrt2\)
Portanto, sabendo a medida do lado do quadrado, é possível determinar a diagonal dele, assim como também pode-se encontrar o lado de um quadrado sabendo a medida de sua diagonal.
Diferenças entre área do quadrado e perímetro do quadrado
Como visto, a área do quadrado é a medida da sua superfície. Já o perímetro do quadrado se refere apenas aos lados da figura. Em outras palavras, enquanto a área é a região que a figura ocupa, o perímetro é apenas o contorno dela.
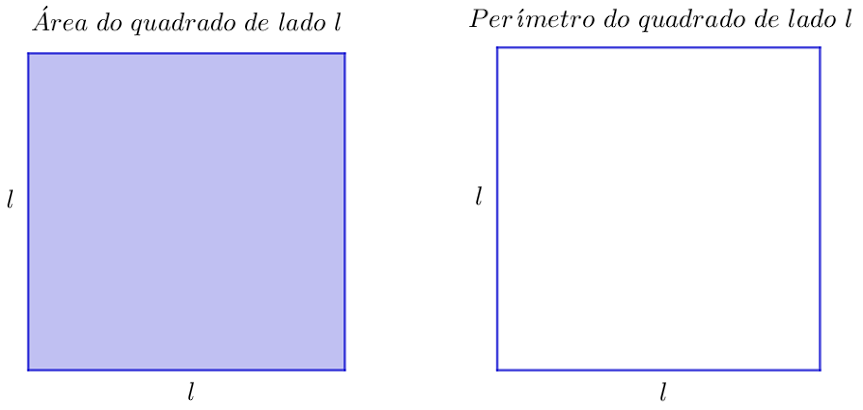
Para calcular o perímetro de um quadrado, basta somar os valores das medidas de seus quatro lados. Assim, como todos os lados de um quadrado possuem uma mesma medida l, temos que:
Perímetro do quadrado = \(l+l+l+l=4l\)
- Exemplo 1: Calcule o perímetro de um quadrado cujo lado mede 11 cm .
Substituindo l=11 na fórmula do perímetro do quadrado, temos:
\(P=4l=4\cdot11=44\ cm\)
- Exemplo 2: Sabendo que o perímetro de um quadrado é de 32 m, determine qual é a medida do lado e a área dessa figura.
Substituindo P=32 na fórmula do perímetro, conclui-se que:
\(P=4l\)
\(32=4l\)
\(l=\frac{32}{4}\ =8\ m\)
Assim, como o lado mede 8 metros, basta utilizar essa medida para descobrir a área desse quadrado:
\(A=l^2=(8\ m)^2=64\ m^2\)
Leia também: Como se calcula a área do retângulo?
Exercícios resolvidos sobre a área do quadrado
Questão 1
A diagonal de um quadrado mede \(5\sqrt2\ cm\). O perímetro P e a área A desse quadrado medem:
a) \(P=20\ cm\) e \(A=50\ cm\ ^2\)
b) \(P=20\sqrt2\ cm\) e \(A=50\ cm^2\)
c) \(P=20\ cm\) e \(A=25\ cm^2\)
d) \(\ P=20\sqrt2\ cm\ \) e \(A=25\ cm^2\)
Resolução: letra C
Sabendo que a diagonal do quadrado mede \(5\sqrt2\ cm\), podemos encontrar a medida do lado do quadrado pela relação:
\(d=l\sqrt2\)
\(5\sqrt2=l\sqrt2\rightarrow l=5\ cm\)
Descoberta a medida do lado do quadrado, podemos substituir esse valor nas fórmulas de perímetro e área do quadrado, obtendo:
\(P=4\cdot l=4\cdot5=20\ cm\)
\(A=l^2=5^2=25\ cm^2\)
Questão 2
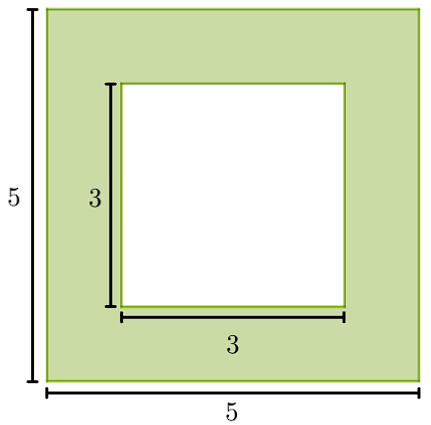
A imagem a seguir é composta por dois quadrados, um cujo lado mede 5 cm e outro cujo lado mede 3 cm:
Qual é a área da região destacada em verde?
a) 9 cm2
b) 16 cm2
c) 25 cm2
d) 34 cm2
Resolução: letra B
Note que a área destacada em verde representa a área do quadrado maior (de lado 5 cm ) menos a área do quadrado menor (de lado 3 cm ).
Portanto, a área destacada em verde mede:
Área do quadrado maior–área do quadrado menor = \(5^2-3^2=25-9=16\ cm^2\)
Fontes:
REZENDE, E.Q.F.; QUEIROZ, M. L. B. de. Geometria Euclidiana Plana: e construções geométricas. 2ª ed. Campinas: Unicamp, 2008.
SAMPAIO, Fausto Arnaud. Trilhas da matemática, 7º ano: ensino fundamental, anos finais. 1. ed. São Paulo: Saraiva, 2018.