Existem duas definições atribuídas à palavra ângulo: a primeira refere-se a um conjunto de pontos situado entre duas semirretas de mesma origem; e a segunda diz respeito à medida entre esses dois segmentos de reta. Sendo assim, ângulos são valores numéricos que representam uma abertura. O mínimo que essa medida pode assumir é zero e sua unidade de medida é o grau.
Quando duas semirretas formam um ângulo de 0° (zero grau), não existe abertura entre elas e sua representação gráfica coincide com a de uma única semirreta. Quando duas semirretas estão em sua abertura máxima, cuja medida é 360°, a imagem formada também é uma única semirreta, mas com um ângulo partindo dessa semirreta e dando a volta em sua origem.
Para compreender melhor, observe a imagem abaixo: à esquerda, um ângulo de 0° e, à direita, um ângulo de 360°.
.jpg)
Qualquer ângulo entre 0° e 360° terá uma forma parecida com o que encontramos na imagem a seguir:
.jpg)
Nessa figura, observe que a origem das semirretas é o ponto O.
Para representar ângulos, podemos usar letras minúsculas, letras gregas minúsculas ou a mesma letra que representa a origem, mas que deve ser maiúscula e com acento circunflexo (Ô).
Como medir ângulos
A régua serve para medir linhas retas que possuem início e fim. Perceba que os ângulos não podem ser medidos com réguas ou qualquer objeto usado para medir comprimento. Observe na figura a seguir uma tentativa de medir o ângulo de 60° com uma régua:
.jpg)
Note que, quanto mais longe da origem a medida é feita, maior é o resultado encontrado. Na verdade, ângulos possuem medidas circulares e, por isso, precisam de um objeto circular para que sua medida seja realizada:
.jpg)
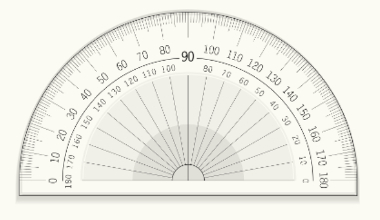
Transferidor: objeto usado para medir ângulos.
Para medir um ângulo, coloque seu vértice (a origem dos segmentos de reta) no centro do transferidor de modo que um dos segmentos de reta aponte para zero. Geralmente, há um ponto que indica o local onde essa origem deve ser colocada. Depois disso, basta observar para onde aponta o outro segmento de reta no transferidor:
.jpg)
Medida de um ângulo feita com um transferidor.
Note que há duas sequências de números no transferidor: uma no sentido horário e outra no sentido anti-horário. Para que a medida fique correta, se o zero escolhido for o do sentido horário, o ângulo para o qual apontará a segunda semirreta estará no mesmo sentido.
Ângulos notáveis
São os mais comuns no cotidiano e acabam facilitando os cálculos matemáticos que os envolvem. São eles:
- Ângulo raso: ângulo que mede 180°, que é metade da abertura máxima que um ângulo pode ter. Os ângulos rasos fazem com que as semirretas formem uma única reta.
- Ângulo reto: ângulo de 90°, que é metade de um ângulo raso e um quarto da abertura total que um ângulo pode ter. O ângulo reto pode ser observado em encontros de parede com o solo, em quinas de mesas, janelas etc.
- Ângulos de 30°, 45° e 60°. Esses ângulos não possuem nome especial, mas são encontrados com frequência na natureza e nas construções humanas.
.jpg)
Exemplos de ângulos retos, rasos, 30°, 45° e 60°
Videoaulas relacionadas: