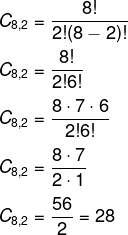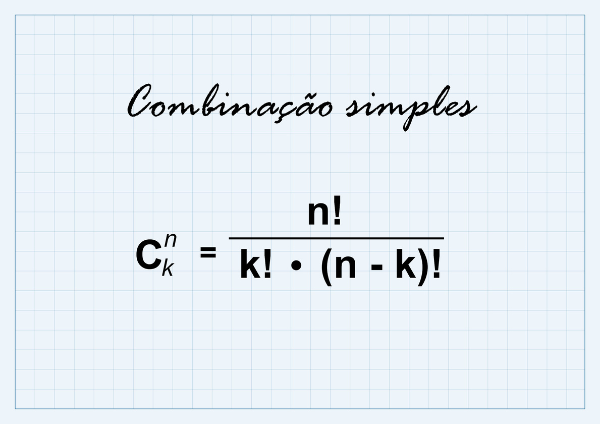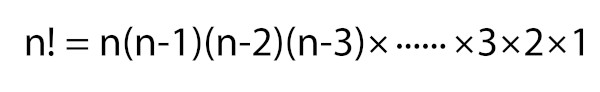A análise combinatória é a área da matemática que desenvolve métodos de contagem aplicados para analisar a quantidade de reagrupamentos possíveis dos elementos de um conjunto em determinadas condições. Na análise combinatória, existem formas diferentes de agrupamentos, e todos eles podem ser resolvidos com o princípio fundamental da contagem, conhecido também como princípio multiplicativo. Tendo como base o princípio multiplicativo, foi possível desenvolver fórmulas diferentes para cada um dos tipos de agrupamento.
Além de problemas comuns de contagem, existem os três tipos de agrupamentos:
- permutação
- combinação
- arranjo
Em situações-problemas em que se aplica técnicas de contagem, é importante analisar e saber diferenciar o tipo de agrupamento que está sendo resolvido, já que, para cada um, há métodos específicos para encontrar-se o total de reagrupamentos possíveis. Na análise combinatória, é importante também saber calcular o fatorial de um número, que nada mais é que a multiplicação desse número por todos os seus sucessores naturais diferentes de zero.
Além de uma vasta aplicação em outras áreas do conhecimento, como a biologia e a química, na própria matemática existem aplicações de técnicas de contagem desenvolvidas pela análise combinatória em situações que envolvem o estudo da probabilidade, essencial na tomada de decisões.
Leia também: Análise combinatória no Enem: como esse tema é cobrado?
Tópicos deste artigo
- 1 - Qual é a função da análise combinatória?
- 2 - Princípio fundamental da contagem
- 3 - Fatorial de um número
- 4 - Tipos de agrupamentos
- 5 - Exercícios resolvidos
Qual é a função da análise combinatória?
A análise combinatória possui várias aplicações, como na probabilidade e estatística, e essas três áreas auxiliam de forma direta as tomadas de decisões. Um exemplo bastante presente se dá na análise das contaminações em uma pandemia e na estimativa das futuras contaminações. A análise combinatória está presente também no estudo da genética ou até mesmo no nosso CPF, que é único em território nacional, além de senhas e sistemas de segurança, que analisam as combinações possíveis para maior proteção.
A análise combinatória está presente também em jogos de loteria, de poker, entre outros jogos de tabuleiros. Em resumo, ela tem como função encontrar todos os agrupamentos possíveis dentro de um conjunto por meio de condições pré-determinadas, além disso, na maioria das vezes, o interesse é saber a quantidade de agrupamentos possíveis, valor que conseguimos encontrar utilizando as ferramentas desse tipo de análise.
Princípio fundamental da contagem
O princípio fundamental da contagem, conhecido também como princípio multiplicativo, é a base para os cálculos envolvendo contagem de reagrupamentos. Ainda que existam fórmulas específicas para calcular alguns casos de agrupamentos, elas surgem desse princípio, conhecido também como P.F.C.
O princípio fundamental da contagem diz que:
Se uma decisão a pode ser tomada de n formas e uma decisão b pode ser tomada de m formas, e essas decisões são independentes, então o número de combinações possíveis entre essas duas decisões é calculado pela multiplicação n · m.
Exemplo:
Márcia vai viajar da cidade A para a cidade C, mas, durante o percurso, ela decidiu que passará pela cidade B para visitar alguns parentes. Sabendo que há 3 rotas para ir da cidade A para a cidade B, e que há 5 rotas para ir da cidade B para a cidade C, de quantas maneiras distintas Márcia pode fazer essa viagem?
Há duas decisões a serem tomadas, d1 → rota entre as cidades A e B; e d2 → rota entre as cidades B e C.
Assim a primeira decisão pode ser tomada de 3 maneiras, e a segunda, de 5 maneiras, logo, basta multiplicar 3 × 5 = 15.
Veja também: Quais são as operações com conjuntos?
Fatorial de um número
Em problemas envolvendo análise combinatória, é bastante comum aparecer o cálculo do fatorial de um número, que nada mais é que a multiplicação de um número por todos os seus sucessores maiores que zero. Representamos o fatorial de um número n por n! (n fatorial).
n! = n . (n-1) . (n-2) . … 3 . 2 . 1
Exemplos:
6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
8! = 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 40.320
Tipos de agrupamentos
Existem problemas que são resolvidos pela aplicação do princípio multiplicativo, entretanto, em muitos casos, convém analisar mais a fundo, a fim de aplicar uma fórmula específica ao problema de acordo com o tipo de agrupamento que estamos resolvendo.
Existem três tipos de agrupamento que são igualmente importantes, são eles a permutação, a combinação e o arranjo. Compreender as características de cada um é essencial para resolver situações-problemas que envolvam qualquer um deles.
-
Permutação
Dado um conjunto com n elementos, chamamos de permutação todos os agrupamentos ordenados formados com esses n elementos, por exemplo, em situações envolvendo filas, em que queremos saber de quantas maneiras uma fila pode ser organizada, em problemas envolvendo anagramas, entre outros.
Para diferenciar a permutação da combinação e do arranjo, é importante entender, na permutação, que a ordem dos elementos é importante e que todos os elementos do conjunto farão parte desses reordenamentos.
Para calcular a permutação de n elementos, utilizamos a fórmula:
Pn = n!
Exemplo:
De quantas maneiras 6 pessoas podem se organizar em uma fila?
Pelo princípio multiplicativo, sabemos que 6 decisões serão tomadas. Sabemos que há 6 possibilidades para a primeira pessoa, 5 possibilidades para a segunda pessoa, 4 possibilidades para a terceira pessoa, 3 possibilidades para a quarta pessoa, 2 para a quinta pessoa, e, por fim, 1 possibilidade para a última, mas perceba que, ao multiplicar as decisões, estamos calculando nada mais que 6!, sendo assim, sabemos que:
P6 = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Exemplo 2:
Quantos anagramas existem na palavra Marte?
O anagrama nada mais é que o reordenamento das letras de uma palavra, ou seja, vamos permutar as letras de lugar. Como a palavra Marte possui 5 letras, então, o total de anagramas pode ser calculado por:
P5 = 5!
P5 = 5 · 4 · 3 · 2 · 1 = 120
-
Arranjo
Um agrupamento é conhecido como arranjo quando selecionamos parte dos elementos dentro de um conjunto. Seja n a quantidade de elementos de um conjunto, o calculo do arranjo é a quantidade de agrupamentos ordenados que conseguimos formar com p elementos desse conjunto, em que n > p.
![]()
Lê-se: arranjo de n elementos tomados de p em p.
Exemplo:
10 atletas estão disputando uma corrida de 100 metros rasos, de quantas maneiras distintas podemos ter o pódio, supondo que os atletas sejam igualmente qualificados e sabendo que ele é formado pelo primeiro, segundo e terceiro lugares?
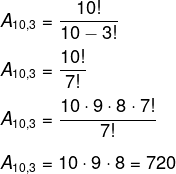
-
Combinação
Calcular as combinações possíveis é contar quantos subconjuntos podemos formar com parte dos elementos do conjunto. Diferentemente do arranjo e da permutação, na combinação, a ordem não é importante, então, o conjunto não é ordenado. Para calcular a combinação, utilizamos a fórmula:
![]()
Exemplo:
Para comemorar o sucesso em vendas de uma corretora de imóveis, a empresa decidiu sortear, entre os 10 funcionários que mais venderam, 4 deles para viajarem para a cidade de Caldas Novas-GO, com a sua família e todas as despesas pagas. Quantos resultados distintos podemos ter com esse sorteio?
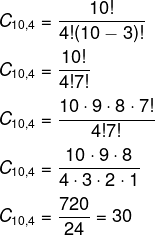
Acesse também: Como estudar Matemática para o Enem?
Exercícios resolvidos
Questão 1 – (Enem) O diretor de uma escola convidou os 280 alunos de terceiro ano a participarem de uma brincadeira. Suponha que existem 5 objetos e 6 personagens numa casa de 9 cômodos; um dos personagens esconde um dos objetos em um dos cômodos da casa. O objetivo da brincadeira é adivinhar qual objeto foi escondido por qual personagem e em qual cômodo da casa o objeto foi escondido.
Todos os alunos decidiram participar. A cada vez, um aluno é sorteado e dá a sua resposta. As respostas devem ser sempre distintas das anteriores, e um mesmo aluno não pode ser sorteado mais de uma vez. Se a resposta do aluno estiver correta, ele é declarado vencedor e a brincadeira é encerrada.
O diretor sabe que algum aluno acertará a resposta porque há
A) 10 alunos a mais do que possíveis respostas distintas.
B) 20 alunos a mais do que possíveis respostas distintas.
C) 119 alunos a mais do que possíveis respostas distintas.
D) 260 alunos a mais do que possíveis respostas distintas.
E) 270 alunos a mais do que possíveis respostas distintas.
Resolução
Alternativa A
Pelo princípio fundamental da contagem, sabemos que o número de respostas distintas é calculado pelo produto 5 × 6 × 9 = 270. Como há 280 alunos, então, temos 10 alunos a mais que possíveis respostas distintas.
Questão 2 – Uma filial de uma empresa de consórcio decidiu selecionar dois funcionários para irem até a matriz conhecer o novo sistema voltado para o departamento de contemplação de consórcios. Para isso, o gerente decidiu realizar um sorteio entre os 8 funcionários do departamento, a fim de decidir quais participariam dessa formação. Sabendo disso, o número de resultados possíveis para esse torneiro é:
A) 42
B) 56
C) 20
D) 25
E) 28
Resolução
Alternativa E
Note que esse é um problema de combinação, pois a ordem não é importante e estamos selecionando parte do conjunto. Vamos calcular a combinação de 8 tomados de dois em dois.