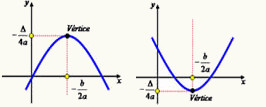
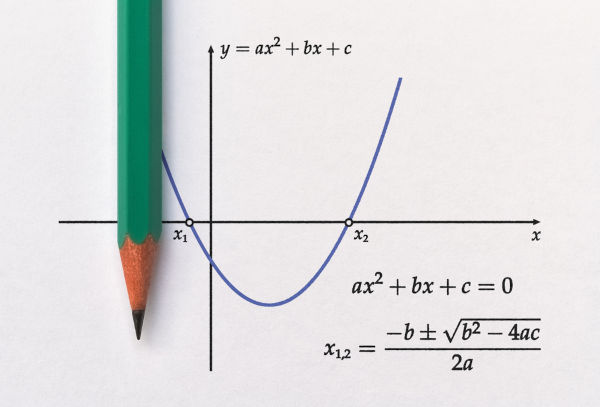
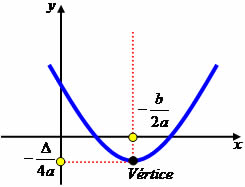
A função que possui a lei de formação f(x) = ax² + bx + c, é considerada do 2º grau e possui como gráfico representativo uma parábola. Ao construirmos o gráfico de uma função com essas características, temos que de acordo com a lei de formação a parábola assume concavidade voltada para cima quando o coeficiente a é maior que zero e concavidade voltada para baixo quando o coeficiente a é menor que zero.
Uma característica dependente do valor do coeficiente a, está ligado à abertura da parábola. À medida que o valor absoluto do coeficiente do termo x² aumenta de valor a abertura fecha e à medida que diminui a abertura se torna maior.

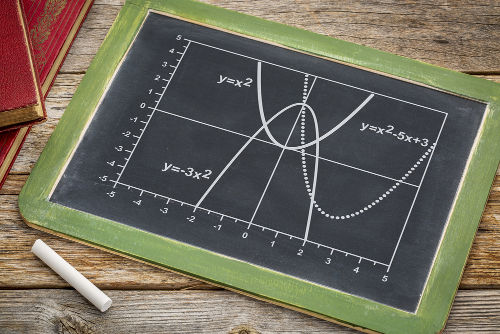
As parábolas a seguir representam as seguintes funções:
Concavidade voltada para cima
y = 9x²
y = 8x²
y = 4x²
y = 2x²
y = x²
y = 0,5x²
Concavidade voltada para baixo
y =- 9x²
y = -8x²
y = -4x²
y = -2x²
y = -x²
y = -0,5x²