Para que um polígono seja considerado regular, ele precisa cumprir três pré-requisitos: ser convexo, ter todos os lados congruentes e ter todos os ângulos internos com a mesma medida. Existe uma fórmula que pode ser usada para calcular a área de qualquer polígono regular, entretanto, é importante conhecer os procedimentos usados para chegar a ela, pois eles demonstram como podemos obter um mesmo resultado sem haver a necessidade de decorar essa fórmula.
Fórmula
A fórmula para calcular a área do polígono regular é a seguinte:
A = P·a
2
Em que P é o perímetro do polígono e a é seu apótema. Note que o perímetro do polígono é dividido por 2 na fórmula. Metade de um perímetro é o que conhecemos como semiperímetro. Assim sendo, a fórmula usada para calcular a área de um polígono regular pode ser compreendida como:
O produto do semiperímetro do polígono regular pelo apótema.
Demonstração da fórmula
Como exemplo, usaremos o heptágono regular. Encontre o centro desse polígono e ligue esse ponto a cada vértice da figura, como o que foi feito na imagem abaixo:
É possível mostrar que todos os triângulos obtidos por esse procedimento são isósceles e congruentes. Tomando o triângulo ABH como exemplo, os lados AH e AB são congruentes e o lado AB é a base do triângulo isósceles.
Nesse mesmo triângulo, construímos o apótema: segmento que vai do centro do polígono até o ponto médio de um de seus lados. O comprimento do apótema será representado pela letra a.
Como esse polígono é regular, o apótema é também a altura do triângulo isósceles. Assim, para calcular a área do triângulo ABH, poderemos usar a seguinte expressão:
At = b·h
2
Como a base do triângulo é o lado do polígono regular e sua altura é o comprimento do apótema, temos:
At = l·a
2
No caso do heptágono, note que existem sete triângulos isósceles congruentes. Então, a área desse polígono regular será:
A = 7·l·a
2
Agora observe que, se substituirmos o heptágono por um polígono regular qualquer, com n lados, teremos, nessa mesma expressão, o seguinte:
A = n·l·a
2
Como o número de lados multiplicado pelo comprimento de cada um desses lados, no polígono regular, representa seu perímetro (P), concluímos que a fórmula para a área do polígono regular é:
A = P·a
2
Assim, como mencionamos anteriormente, essa demonstração para chegar à fórmula é também uma técnica que pode ser usada para calcular a área do polígono regular.
Exemplo:
Calcule a área de um hexágono regular cujo lado mede 20 cm.
Solução: Para calcular essa área, será necessário saber a medida do apótema e do perímetro do polígono. O perímetro é dado por:
P = 6·20 = 120 cm.
Como a medida do apótema não foi dado, será necessário descobri-lo de alguma maneira. Para isso, primeiramente encontraremos mais informações sobre os triângulos que podem ser construídos a partir do centro do hexágono regular:
A soma dos ângulos internos de um hexágono é igual a 720°, pois:
S = (n – 2)180
S = (6 – 2)180
S = 4·180
S = 720°
Isso significa que cada ângulo interno do polígono mede 120°. Isso acontece porque todos os seus ângulos são iguais, uma vez que o polígono é regular, assim:
720 = 120°
6
Como todos os triângulos construídos no interior do polígono são isósceles e congruentes, pode-se garantir que cada ângulo da base desses triângulos é igual à metade de 120, isto é, 60°. Também pode-se garantir que um triângulo isósceles que possui ângulos da base com 60° é equilátero, ou seja, possui todos os lados com a mesma medida. Assim, teremos as seguintes medidas no hexágono:
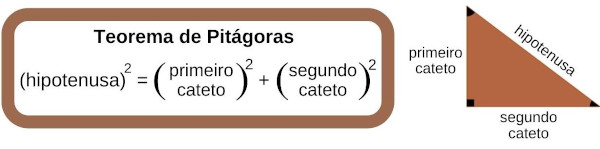
Para encontrar o apótema, basta usar o teorema de Pitágoras ou a Trigonometria.
Sen 60° = a
20
√3 = a
2 20
2a = 20√3
a = 20√3
2
a = 10√3
Agora que sabemos o apótema e o lado, podemos calcular a área do hexágono regular:
A = P·a
2
A = 120·10√3
2
A = 1200√3
2
A = 600√3 cm2