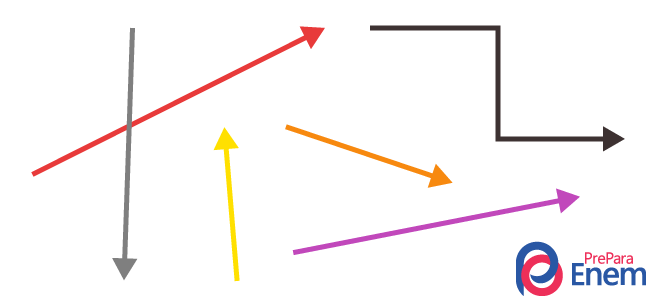
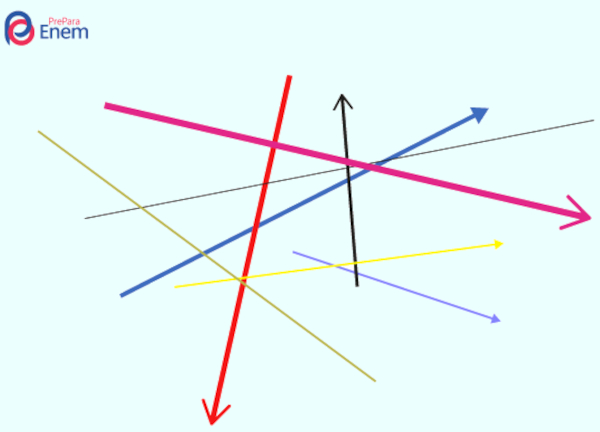
Os vetores são representações de grandezas vetoriais, como módulo, direção e sentidos. Eles são comumente representados por setas e possuem diversos tipos, como: iguais, nulos, opostos ou unitários.
O vetor resultante resulta das operações algébricas que podem ser feitas com vetores. Caso os vetores estejam em uma mesma direção, faz-se a operação de adição, já se estiverem em direções contrárias, faz-se a operação de subtração.
Para vetores perpendiculares, que formam um ângulo de 90°, encontra-se seu vetor resultante usando o teorema de Pitágoras, mas se os vetores forem oblíquos, com um ângulo diferente de 0°, 90° e 180° , usa-se a regra do paralelogramo, para encontrar a orientação do vetor, e a lei dos cossenos, para encontrar seu módulo.
Saiba mais: Grandezas angulares — as grandezas relacionadas aos movimentos circulares
Tópicos deste artigo
- 1 - Resumo sobre vetores
- 2 - Videoaula sobre vetores
- 3 - Grandezas vetoriais e grandezas escalares
- 4 - Módulo, direção e sentido dos vetores
- 5 - O que é vetor resultante?
- 6 - Quais são os tipos de vetores?
- 7 - Operações com vetores
- 8 - Exercícios resolvidos sobre vetores
Resumo sobre vetores
- São segmentos de retas que caracterizam as grandezas vetoriais indicando seu módulo, sentido e direção.
- Seu módulo é seu tamanho; seu sentido, pode ser à direita ou à esquerda; e sua direção pode ser horizontal, vertical ou diagonal.
- Chamamos de vetor resultante o que resulta das operações.
- Podem ser classificados como iguais, nulos, opostos ou unitários.
- Existem diversas operações que podem ser realizadas com eles, como a adição, a subtração ou a multiplicação de um número real por um vetor.
- Podem ser decompostos em duas componentes, uma na horizontal, em x, e uma na vertical, em y.
- Os que são perpendiculares se calcula usando o teorema de Pitágoras, já para os oblíquos, usa-se a regra do paralelogramo e a lei dos cossenos.
Videoaula sobre vetores
Grandezas vetoriais e grandezas escalares
Na Física, há grandezas vetoriais e grandezas escalares, a diferença principal entre elas está na necessidade ou não de orientação.
- Grandezas vetoriais: precisa-se de três informações para caracterizá-las: módulo, direção e sentido. Por exemplo, a força é uma grandeza vetorial, já que se precisa saber para onde ela está atuando, ou seja, se está puxando ou empurrando.
- Grandezas escalares: podem ser caracterizadas apenas com um número seguido de uma unidade de medida. Por exemplo, o tempo é uma grandeza escalar, pois não é necessário saber sua orientação, afinal de contas, o tempo só avança.
Módulo, direção e sentido dos vetores
Na Física, os vetores são segmentos de retas que caracterizam as grandezas vetoriais indicando seu módulo, sentido e direção. São representados por uma letra com seta em cima, como podemos ver abaixo:

A orientação dos vetores consiste em:
- Módulo: indica o comprimento do vetor e é conhecido como o valor numérico, intensidade ou tamanho da grandeza vetorial, pode ser representado por \(\left|\vec{v}\right|\) ou v .
- Direção: indica a direção de localização do vetor, que pode ser horizontal, vertical ou diagonal.
- Sentido: indica o sentido da ponta do vetor, podendo ser à direita, à esquerda, para cima, para baixo, a leste, norte, sul, oeste, entre outros.
O que é vetor resultante?
O vetor resultante é a nomenclatura dada ao vetor que resulta das operações vetoriais. Para encontrá-lo, é necessário considerar o módulo, direção e sentido dos vetores envolvidos na operação.
Quais são os tipos de vetores?
Existem diversos tipos de vetores. Veremos os principais a seguir.
-
Vetores iguais
São assim chamados os vetores cujos segmentos de retas são iguais, com mesma direção, sentido e módulo. Assim:
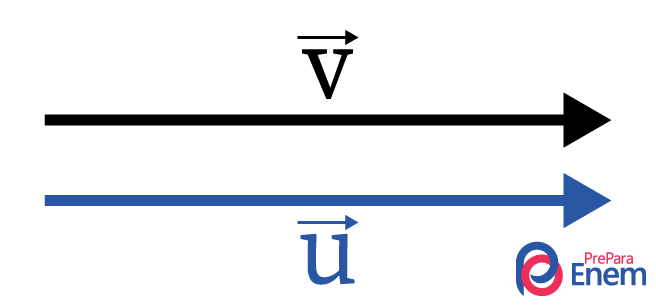
-
Vetores nulos
São os vetores que possuem seu módulo igual a zero, com direção e sentido indefinidos. São representados geometricamente por um ponto e escritos assim: \(\vec{0}\).
- Vetores opostos
São as representações dos vetores em seus sentidos contrários. São representados pelo sinal negativo precedendo o vetor:
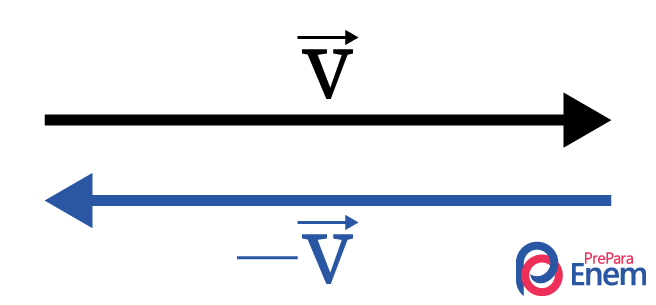
-
Vetores unitários
São aqueles cujo módulo é igual a 1.
Operações com vetores
Existem diversas operações algébricas que se pode realizar usando vetores. Veremos algumas delas a seguir.
-
Adição de vetores
Ocorre quando dois ou mais vetores estão em um mesmo sentido. Consiste na soma de seus módulos e de suas direções.
Exemplo:
Dado um vetor \(\vec{v}\), com tamanho de 2 unidades, e outro vetor \(\vec{u}\), com tamanho de 5 unidades, qual será o vetor resultante da adição entre eles?
Resolução:
Quando se trabalha com vetores, é recomendável sempre fazer o desenho do vetor, já que seus sentidos e direções são importantes para os cálculos.
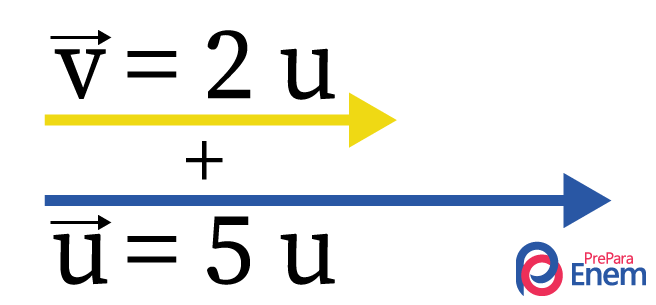
Simultaneamente à soma dos valores dos vetores, faz-se a soma de suas direções, para isso, basta colocar um na frente do outro.
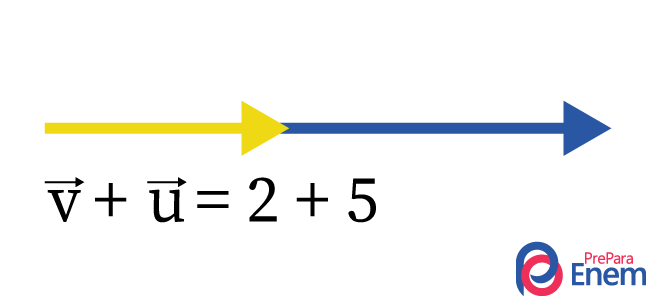
O vetor resultante possui módulo de 7 unidades, sentido à direita e direção horizontal.
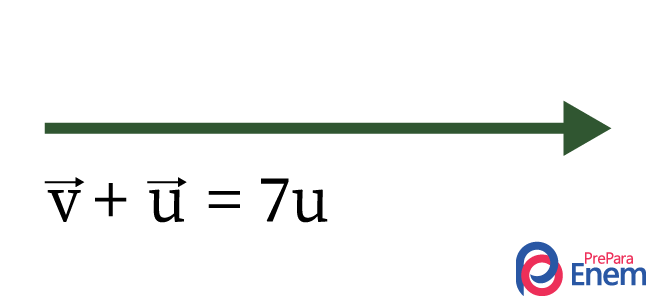
O módulo ou tamanho do vetor resultante é de 7 unidades.
-
Subtração de vetores
Ocorre quando os vetores estão em sentidos opostos, consistindo na diminuição de seus módulos e de suas direções. Vale ressaltar que subtrair dois vetores é o mesmo que somar um vetor com outro de valor oposto, como \(\vec{v}-\vec{u}=\vec{v}+\left(-\vec{u}\right)\) .
Exemplo:
Dado um vetor \(\vec{v}\), com tamanho de 1 unidade, no sentido à direita, e outro vetor \(\vec{u}\), com tamanho de 3 unidades, no sentido à esquerda, qual será o vetor resultante da subtração entre eles?
Resolução:
Desenhando os vetores:
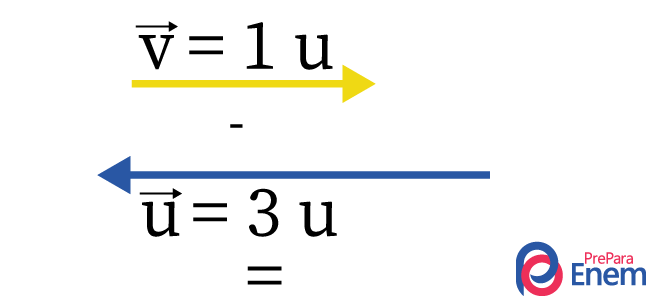
Simultaneamente à subtração dos valores dos vetores, faz-se a subtração de suas direções, para isso basta colocar um abaixo do outro, e o vetor resultante é o que falta para completar o vetor azul \(\vec{u}\).
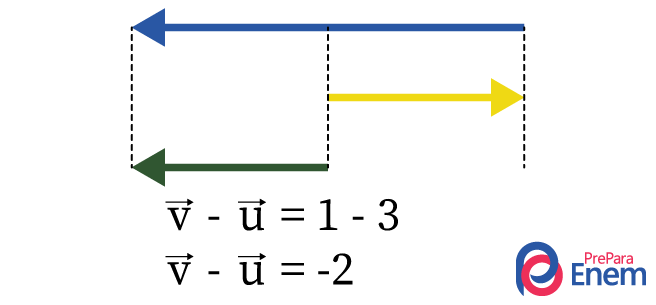
O valor da subtração é de –2, o que significa que o vetor resultante tem sentido contrário ao vetor amarelo \(\vec{v}\). Ele tem módulo de 2 unidades, sentido à esquerda e direção horizontal.
-
Vetores perpendiculares: teorema de Pitágoras
Os vetores perpendiculares ou vetores que, combinados, formam um ângulo de 90° podem ser calculados por meio do teorema de Pitágoras, cuja fórmula é:
\({\mathrm{hipotenusa}}^2={{\mathrm{cateto}}_1}^2+{{\mathrm{cateto}}_2}^2\)
Exemplo:
Dado um vetor \(\vec{v}\) com módulo de 3 unidades e orientação vertical para cima e outro vetor \(\vec{u}\) com módulo de 4 unidades e orientação horizontal à direita, qual será o vetor resultante da soma entre eles?
Resolução:
Desenhando os vetores:
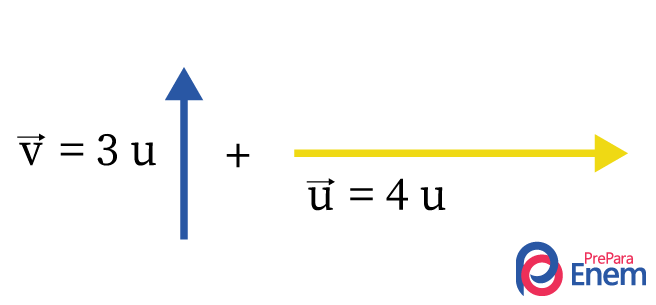
Depois, encontra-se o vetor resultante, para isso, movimenta-se os seus vetores sem alterar seus tamanhos até se encontrarem, e traça-se pontilhados de mesmo tamanho, formando um quadrado. Em seguida, faz-se uma linha diagonal, que corresponde ao vetor resultante \(\vec{R}\) da soma entre esses dois vetores, como desenhado abaixo:
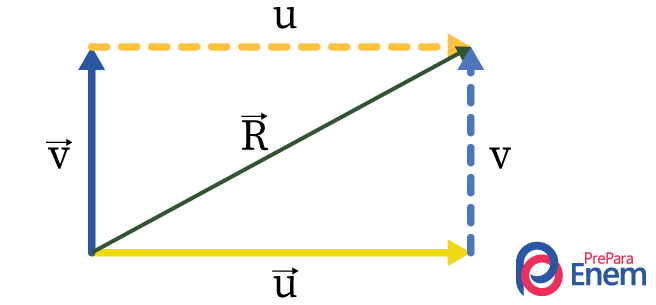
Como já foram encontrados o sentido orientado a nordeste e a direção na diagonal do vetor resultante, falta encontrar o módulo calculado pelo teorema de Pitágoras:
\({\mathrm{hipotenusa}}^2={{\mathrm{cateto}}_1}^2+{{\mathrm{cateto}}_2}^2\)
A hipotenusa corresponde ao módulo do vetor resultante \(\vec{R}\) , e os catetos são os módulos dos vetores envolvidos:
\(R^2=u^2+v^2\)
\(R^2=4^2+3^2\)
\(R^2=16+9\)
\(R^2=25\)
\(R=\sqrt{25}\)
\(R=5\ u\)
O módulo ou tamanho do vetor resultante é de 5 unidades.
-
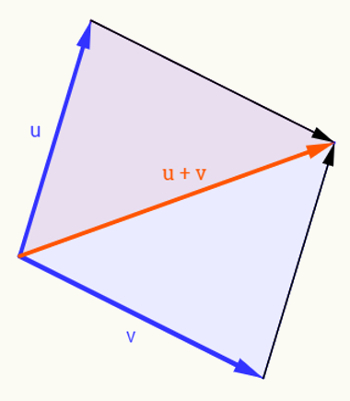
Vetores oblíquos: regra do paralelogramo
São aqueles vetores que, combinados, formam um ângulo diferente de 0° , 90° e 180° . A orientação do vetor resultante é encontrada por meio da regra do paralelogramo, e seu módulo, por meio da lei dos cossenos, cuja fórmula é:
\({\mathrm{hipotenusa}}^2={{\mathrm{cateto}}_1}^2+{{\mathrm{cateto}}_2}^2-2\bullet{\mathrm{cateto}}_1\bullet{\mathrm{cateto}}_2\bullet\cos{\theta}\)
Exemplo:
Dado um vetor \(\vec{v}\) com módulo de 2 unidades e orientação a noroeste e outro vetor \(\vec{u} \) com módulo de 4 unidades e orientação a sudeste, qual será o vetor resultante da soma entre eles, sabendo que o ângulo formado pela sua combinação é de 60° ?
Resolução:
Desenhando os vetores:
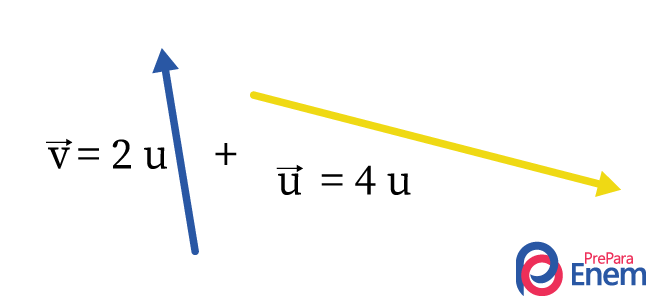
Usando a regra do paralelogramo, encontra-se a orientação do vetor resultante. Essa regra consiste em movimentar os seus vetores sem alterar seus tamanhos até se encontrarem, e traçar pontilhados de mesmo tamanho, formando um quadrado, como nos vetores perpendiculares, mas agora formando um paralelogramo. Depois, faz-se uma linha diagonal, que corresponde ao vetor resultante \(\vec{R} \) da soma entre esses dois vetores, como desenhado abaixo:
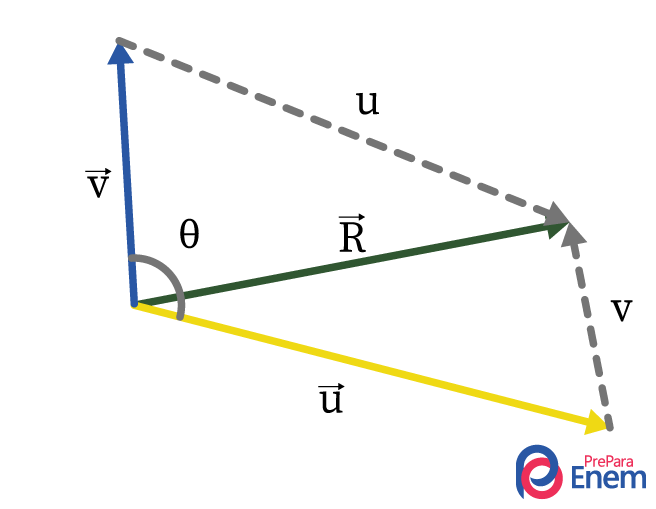
O vetor resultante tem sentido à direita e direção diagonal. Calculamos seu módulo por meio da lei dos cossenos:
\({\mathrm{hipotenusa}}^2={{\mathrm{cateto}}_1}^2+{{\mathrm{cateto}}_2}^2-2\bullet{\mathrm{cateto}}_1\bullet{\mathrm{cateto}}_2\bullet\cos{\theta}\)
A hipotenusa corresponde ao módulo do vetor resultante \(\vec{R}\) e os catetos são os módulos dos vetores envolvidos:
\(R^2=u^2+v^2-2\bullet u\bullet v\bullet\cos{\theta}\)
\(R^2=4^2+2^2-2\bullet4\bullet2\bullet cos60°\)
\(R^2=16+4-16\bullet0,5\)
\(R^2=16+4-8\)
\(R^2=12\)
\(R=\sqrt{12}\)
\(R=2\sqrt3\ u\)
O módulo ou tamanho do vetor resultante é de \(2\sqrt3\) unidades.
-
Resultante de vários vetores
Para encontrar o vetor resultante entre vários vetores, é necessário uni-los em suas origens e depois encontrar a resultante de 2 em 2 vetores. Dependendo dos vetores dados, pode-se calcular o vetor resultante por meio das operações de adição e subtração, do teorema de Pitágoras ou da lei dos cossenos.
Exemplo:
Dados 3 vetores, um vetor \(\vec{v}\) com módulo de 2 unidades e orientação a noroeste, um segundo vetor \(\vec{u}\) com módulo de 3 unidades e orientação a sudeste, e um terceiro vetor \(\vec{t}\) com módulo de 1 unidade com sentido para baixo e direção vertical, qual será o vetor resultante da soma entre eles, sabendo que o ângulo formado entre \(\vec{u}\) e \(\vec{v}\) é de 60° e entre \(\vec{R_{uv}}\) e \(\vec{t}\)é de 30° ?
Resolução:
Desenhando os vetores:
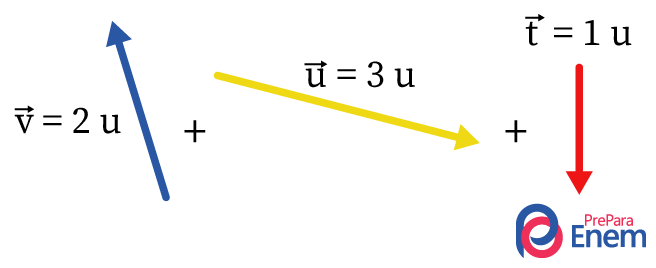
Agora, eles serão unidos em suas origens:
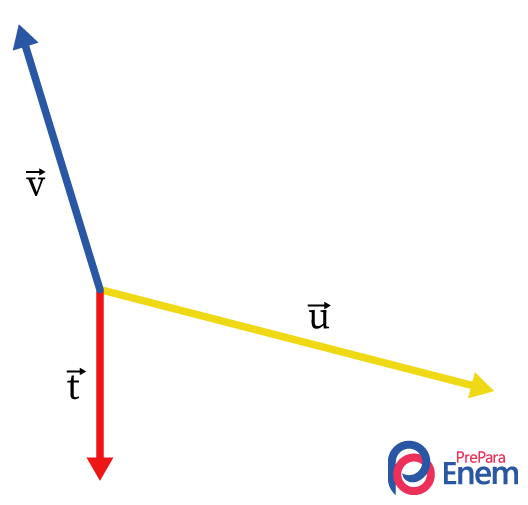
Primeiramente, encontra-se o vetor resultante entre \(\vec{v}\) e \(\vec{u}\), chamado \(\vec{R_{uv}}\), e seu módulo é dado por meio da lei dos cossenos:
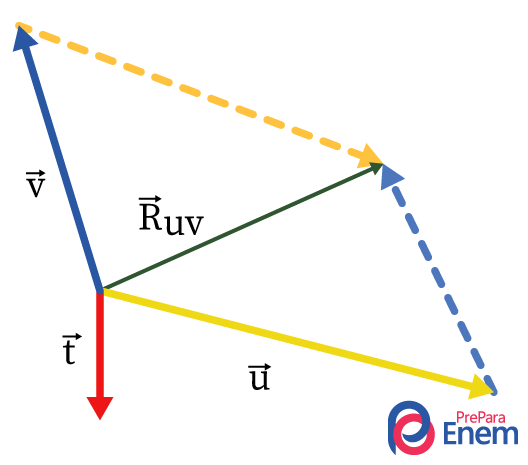
\({R_{uv}}^2=u^2+v^2-2\bullet u\bullet cos60°\)
\({R_{uv}}^2=3^2+2^2-2\bullet3\bullet2\bullet0,5\)
\({R_{uv}}^2=9+4-12\bullet0,5\)
\({R_{uv}}^2=9+4-6\)
\({R_{uv}}^2=7\)
\(R_{uv}=\sqrt7\)
Por fim, encontra-se o vetor resultante \(\vec{R} \) entre o vetor \(\vec{R_{uv}} \) e \(\vec{t}\) e seu módulo é dado por meio da lei dos cossenos:
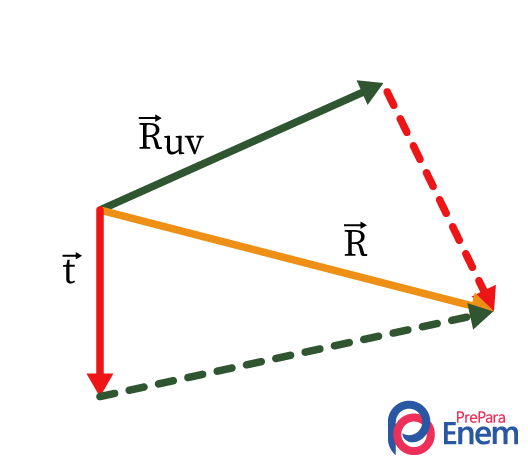
\(R^2={R_{uv}}^2+t^2-2\bullet R_{uv}\bullet cos30°\)
\(R^2={\sqrt7}^2+1^2-2\bullet\sqrt7\bullet1\bullet\frac{\sqrt3}{2}\)
\(R^2=7+1-\sqrt{21}\)
\(R^2=8-4,58\)
\(R^2=3,42\)
\(R\cong1,85\)
O módulo ou tamanho do vetor resultante é de aproximadamente 1,85 unidades.
-
Decomposição vetorial
A decomposição vetorial consiste em encontrar as componentes x e y de algum vetor. Basicamente o que se faz é o processo contrário ao da soma de vetores, em que se encontra aqueles vetores que se somaram e resultaram no vetor resultante.
Se houver um vetor \(\vec{v} \) inclinado e se quer decompô-lo em suas componentes x e y , ele será desenhado da seguinte forma:
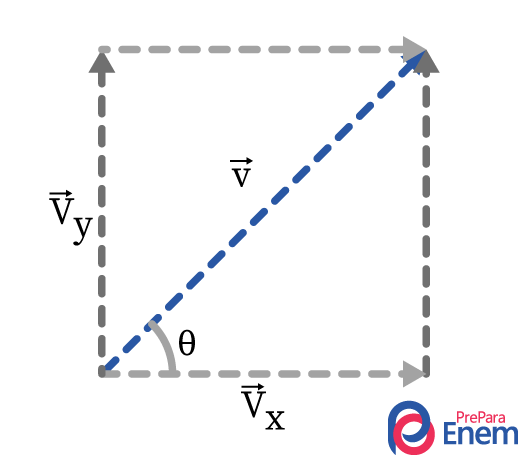
No desenho, \(\vec{v}\) é o vetor resultante da soma vetorial entre \(\vec{v_x}\ \) e \(\vec{v_y}\) . Como se percebe, o desenho forma um triângulo retângulo, como este:
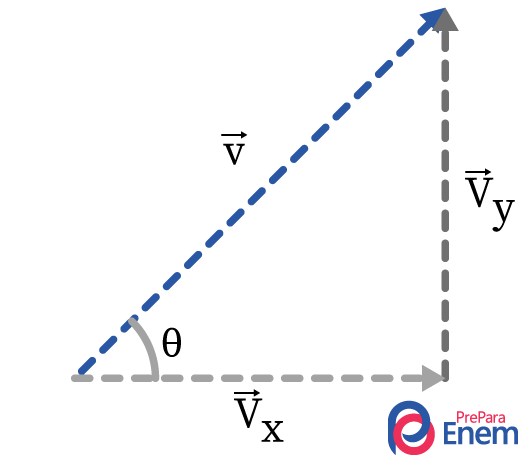
Para calcular o módulo dos vetores \(\vec{v_x}\ \) e \(\vec{v_y}\) , utiliza-se as relações trigonométricas do triângulo retângulo. Primeiramente, encontra-se \(v_y\) :
\(\sin{\theta=\frac{cateto\ oposto}{hipotenusa}}\)
\(\sin{\theta=\frac{v_y}{v}}\)
\(v\bullet\sin{\theta=v_y}\)
Encontrando \(v_x\) :
\(\cos{\theta=\frac{cateto\ adjacente}{hipotenusa}}\)
\(\cos{\theta=\frac{v_x}{v}}\)
\(v\bullet\cos{\theta=v_x}\)
Exemplo:
Uma força é realizada ao puxar um bloco no chão. O módulo da força é de 30 N e tem inclinação de 60° com a horizontal. Quais serão as componentes horizontal e vertical dessa força?
Resolução:
Primeiramente, faz-se o desenho das forças e suas componentes:
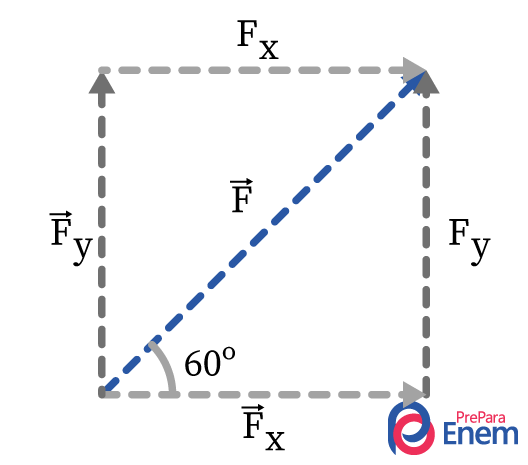
Calculando o módulo da componente horizontal \(F_x\) :
\(F_x=F\bullet cos60°\)
\(F_x=30\bullet0,5\)
\(F_x=15\ N\)
Calculando o módulo da componente vertical \(F_y\) :
\(F_y=F\bullet sin60°\)
\(F_y=30\bullet\frac{\sqrt3}{2}\)
\(F_x=15\sqrt3\ N\)
-
Produto de um número real por um vetor
O produto entre um número real e um vetor resulta em um novo vetor com mesma direção, mesmo sentido, se o número real for positivo, ou sentido contrário, se o número for negativo, e seu módulo será a multiplicação entre o número n e o vetor \(\vec{v}\).
\(v_{novo}=n\bullet\vec{v}\)
Exemplo:
Dado um vetor \(\vec{v}\) com módulo de 5 unidades e orientação a noroeste, qual será seu valor se multiplicado pelo número real 3?
Resolução:
Sua direção e sentido continuam sendo os mesmos, diagonal a noroeste respectivamente. Seu módulo será então:
\(v_{novo}=n\bullet\vec{v}\)
\(v_{novo}=3\bullet5\)
\(v_{novo}=15\ u\)
O módulo ou tamanho do vetor novo é de 15 unidades.
Saiba mais: Ângulo entre dois vetores — como medir?
Exercícios resolvidos sobre vetores
Questão 1
(UEPG – PR) Quando dizemos que a velocidade de uma bola é de 20 m/s, horizontal e para a direita, estamos definindo a velocidade como uma grandeza:
A) escalar
B) algébrica
C) linear
D) vetorial
E) n.d.a.
Resolução:
Alternativa D
Como a grandeza velocidade possui direção, sentido e intensidade, diz-se que ela é vetorial.
Questão 2
Os vetores\(\vec{a}\) , \(\vec{b} \) e \(\vec{c} \) têm módulos iguais a 3, 6 e 9 respectivamente. Qual o módulo do vetor \(\vec{s}=\vec{a}+\vec{b} \) e do vetor \(\vec{v}=\ \vec{s}+\vec{c}\) ?
A) 12, 12
B) 15, 18
C) 9, 18
D) 0, 18
E) 9, 12
Resolução:
Alternativa C
O módulo do vetor \(\vec{s}\)é a soma dos vetores \(\vec{a} \) e \(\vec{b}\) , então:
\(\vec{s}=\vec{a}+\vec{b}\)
\(\vec{s}=3+6\)
\(\vec{s}=9\)
Já o módulo do vetor \(\vec{v}\) é a soma dos vetores \(\vec{s}\) e \(\vec{c}\) , então:
\(\vec{v}=\ \vec{s}+\vec{c}\)
\(\vec{v}=\ 9+9\)
\(\vec{v}=18\)