A velocidade vetorial é a velocidade de um corpo em termos vetoriais, em razão disso, apresenta módulo, direção e sentido. É calculada pela divisão entre a variação do deslocamento vetorial e o intervalo de tempo necessário para ocorrer esse movimento.
Leia também: Velocidade terminal — a máxima velocidade atingida por um objeto em queda livre
Resumo sobre a velocidade vetorial
-
Sua unidade de medida é metros por segundo.
-
Seu sentido pode ser vertical, diagonal ou horizontal.
-
Sua direção pode ser para cima, para baixo, para esquerda ou para a direita.
-
Pode ser positiva ou negativa de acordo com seu movimento no plano cartesiano.
-
Seu módulo é a velocidade escalar.
-
Na velocidade média vetorial, calculamos a velocidade em parâmetros vetoriais.
-
Na velocidade vetorial instantânea, calculamos a velocidade em tempos próximos a zero.
Tópicos deste artigo
- 1 - O que é velocidade vetorial?
- 2 - Como se calcula a velocidade vetorial?
- 3 - Velocidade vetorial x velocidade escalar
- 4 - Velocidade média vetorial
- 5 - Velocidade vetorial instantânea
- 6 - Exercícios resolvidos sobre velocidade vetorial
O que é velocidade vetorial?
A velocidade vetorial é uma grandeza física vetorial que mede a rapidez com que ocorre o deslocamento vetorial de um objeto durante um tempo específico. Sua unidade de medida, de acordo com o Sistema Internacional de Unidade (S.I.), é o metros por segundo, contudo, em nosso cotidiano, é comum vermos a velocidade sendo representada por quilômetros por hora.
Por ser uma grandeza física vetorial, ela apresenta orientação e módulo:
-
Direção: pode ser horizontal, vertical ou diagonal.
-
Sentido: a velocidade será positiva quando seu sentido de movimento for para cima e/ou para a direita; a velocidade será negativa quando seu sentido de movimento for para baixo e/ou para a esquerda, de acordo com o plano cartesiano.
-
Módulo ou intensidade: calculado pela fórmula da velocidade vetorial.
A fórmula da velocidade vetorial é:
\(\vec{v}=\frac{∆\vec{x}}{∆t}\)
-
\(\vec{v}\) é a velocidade vetorial, medida em \([m/s] \).
-
\(∆\vec{x}\) é a variação de deslocamento vetorial, diferença entre \(\vec{x}\) e \(\vec{x}_o\), medida em metros \([m] \).
-
\(\vec{x}\) é o par ordenado de (x,y) final, medido em metros \([m] \).
-
\(\vec{x}_o\) é o par ordenado de (x,y) inicial, medido em metros \([m] \).
-
\(∆t \) é a variação de tempo, medida em segundos \([s] \).
-
t é o tempo final, medido em segundos \([s] \).
-
\(t_o \) é o tempo inicial, medido em segundos \([s] \).
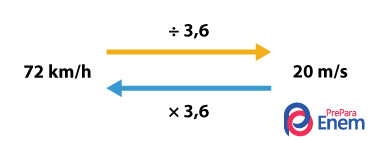
Para convertermos de quilômetros por hora para metros por segundo, precisamos dividir a velocidade dada em km/h por 3,6; se quisermos transformar de metros por segundo para quilômetros por hora, basta multiplicar a velocidade dada em m/s por 3,6. Como podemos ver no exemplo abaixo:
Como se calcula a velocidade vetorial?
A velocidade vetorial pode ser calculada pela sua fórmula, que envolve a variação de deslocamento vetorial e o tempo. Contudo, de acordo com as informações dadas a respeito do vetor deslocamento, existem diversas formas de resolvê-lo.
Geralmente o vetor deslocamento é dado pela variação entre os vetores \(\vec{x}_o\) e \(\vec{x}\), sendo:
\(∆\vec{x}=\vec{x}-\vec{x}_o\)
-
\(∆\vec{x}\) é a variação de deslocamento vetorial, diferença entre \(\vec{x}\) e \(\vec{x}_o\), medida em metros \([m] \).
-
\(\vec{x}\) é o par ordenado de \( (x,y) \) final, medido em metros \([m] \).
-
\(\vec{x}_o\) é o par ordenado de \( (x,y) \) inicial, medido em metros \([m] \).
Contudo, se o ângulo entre os vetores \(\vec{x}_o\) e \(\vec{x}\) for relevante para o exercício, o vetor deslocamento \(\mathbf{∆\vec{x}}\) é calculado de acordo com a tabela abaixo:
|
Ângulo entre os vetores \(\mathbf{\vec{x}_o}\) e \(\mathbf{\vec{x}}\) |
Fórmula do vetor deslocamento |
Nome do teorema ou regra |
|
0° e vetores na mesma direção |
\(∆\vec{x}=\vec{x}_o+\vec{x}\) |
Adição dos vetores |
|
90° |
\(∆\vec{x}^2=\vec{x}_o^2+\vec{x}^2\) |
|
|
180° e vetores na mesma direção |
\(∆\vec{x}=\vec{x}_o-\vec{x}\) |
Subtração dos vetores |
|
Não informou o ângulo |
\(∆\vec{x}=\vec{x}+\vec{x}_o\) |
Variação de deslocamento |
|
Ângulos diferentes de 0°,90° e |
\(∆\vec{x}^2=\vec{x}_o^2+\vec{x}^2-2\cdot \vec{x}_o\cdot \vec{x}\cdot cosθ\) |
-
\(∆\vec{x}\) é a variação de deslocamento vetorial, diferença entre \(\vec{x}\) e \(\vec{x}_o\), medida em metros \( [m] \).
-
\(\vec{x }\) é o par ordenado de \( (x,y) \) final, medido em metros \( [m] \).
-
\(\vec{x}_o \) é o par ordenado de \((x,y) \) inicial, medido em metros \([m] \).
-
\(θ \) é o ângulo entre \(\vec{x}_o\) e \(\vec{x}\), medido em graus \( [°] \).
Exemplo 1: Um carro se locomove 5 metros ao norte e depois vira à direita e se desloca por mais 15 metros, durante 0,5 segundos. Qual é a variação de deslocamento vetorial e a sua velocidade vetorial?
Para facilitar na visualização, desenharemos a locomoção do carro pelos vetores amarelo e azul; entre eles há um ângulo de 90°:
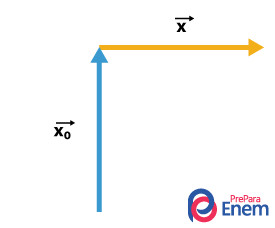
Para encontrarmos o vetor variação de deslocamento, é necessário primeiramente usarmos a regra do paralelogramo, em que criamos um novo vetor, em roxo, que corresponde à soma entre os vetores amarelo e azul, como podemos ver abaixo:
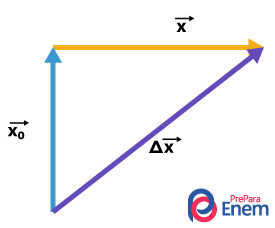
Posteriormente, usamos o teorema de Pitágoras, já que o ângulo entre os vetores \(\vec{x}_o\) e \(\vec{x}\) é de 90°, para encontrar o valor da variação de deslocamento vetorial.
\(hipotenusa^2=cateto^2+cateto^2\)
\(∆\vec{x}^2=\vec{x}_o^2+\vec{x}^2\)
De acordo com o enunciado, temos que \(\vec{x}_o=5\ m\) e \(\vec{x} = 15\ metros\):
\(∆\vec{x}^2=5^2+15^2\)
\(∆\vec{x}^2=25+225\)
\(∆\vec{x}^2=250\)
\(∆\vec{x}^2=\sqrt{250}\)
\(∆\vec{x}^2=5\sqrt{10}\)
Como o carro se deslocou \(5\sqrt{10}\) metros, em 0,5 segundos, é possível encontrarmos o valor da sua velocidade vetorial.
\(\vec{v}=\frac{∆\vec{x}}{∆t}\)
\(\vec{v}=\frac{5\sqrt{10}}{0,5}\)
\(\vec{v}=\frac{\sqrt{10}}{0,1}\)
\(v≈31,62\ m/s\)
Então a velocidade vetorial do carro foi de aproximadamente 31,62 metros por segundo.
Exemplo 2: Uma pessoa se desloca 800 metros a nordeste e depois mais 500 metros a leste, sabendo que o ângulo θ vale 150°, qual é a sua variação de deslocamento vetorial?
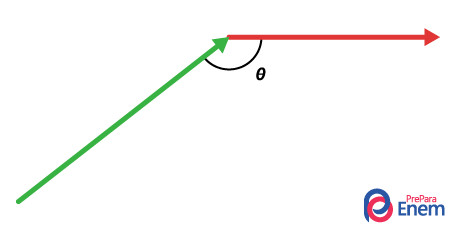
Da mesma forma do exemplo anterior, para encontrarmos o vetor variação de deslocamento entre os vetores verde e vermelho, é necessário primeiramente usarmos a regra do paralelogramo, pela qual criamos um novo vetor, em roxo, que corresponde à soma entre esses vetores, como podemos ver abaixo:
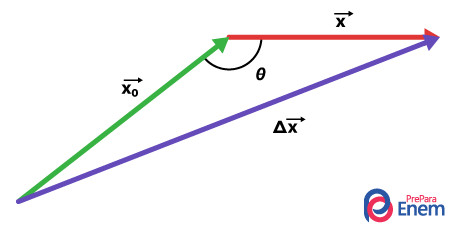
Como nos foi informado o ângulo como sendo de 150°, encontraremos a variação de deslocamento vetorial por meio da lei dos cossenos:
\(∆\vec{x}^2=\vec{x}_o^2+\vec{x}^2-2\cdot \vec{x}_o\cdot \vec{x}\cdot cosθ\)
De acordo com o enunciado, temos que \(\vec{x}_o=800\ m \) e \(\vec{x}=500\ m \):
\(∆\vec{x}^2=800^2+500^2-2\cdot800\cdot 500\cdot cos150°\)
\(∆\vec{x}^2=640.000+250.000-800.000\cdot cos150°\)
O cos150° equivale a \(-cos30°≈-0,866\), então:
\(∆\vec{x}^2=640.000+250.000-800.000\cdot (-0,866)\)
\(∆\vec{x}^2=640.000+250.000+692.800\)
\(∆\vec{x}^2=1.582.800\)
\(∆\vec{x}=\sqrt{1.582.800}\)
\(∆\vec{x}≈1258,09\ metros\)
Então a variação de deslocamento vetorial da pessoa foi de aproximadamente 1258,09 metros.
Saiba mais: Operações básicas envolvendo vetores
Velocidade vetorial x velocidade escalar
É comum vermos os termos velocidade escalar e velocidade vetorial, mas a principal diferença entre eles é que esta se trata do quanto se deslocou vetorialmente durante um tempo estabelecido, enquanto aquela se trata do módulo da velocidade vetorial.
Velocidade média vetorial
A velocidade média vetorial é similar à definição de velocidade média, contudo, o seu estudo envolve vetores, em razão disso, é possível termos velocidade nula, ainda que haja movimento, já que o corpo pode ter se deslocado durante um tempo e depois voltar ao ponto de partida.
A fórmula da velocidade média vetorial é:
\(\vec{v}_m=\frac{∆\vec{x}}{∆t}=\frac{\vec{x}-\vec{x}_o}{t-t_o}\)
-
\(\vec{v}_m\) é a velocidade média vetorial, medida em \( [m/s] \).
-
\(∆\vec{x}\) é a variação de deslocamento vetorial, diferença entre \(\vec{x}\) e \(\vec{x}_o\), medida em metros \( [m] \).
-
\(\vec{x}\) é o par ordenado de (x,y) final, medido em metros \([m] \).
-
\(\vec{x}_o\) é o par ordenado de (x,y) inicial, medido em metros \( [m] \).
-
\(∆t\) é a variação de tempo, medida em segundos \([s] \).
-
t é o tempo final, medido em segundos \([s] \).
-
\(t_o\) é o tempo inicial, medido em segundos \([s] \).
Velocidade vetorial instantânea
A velocidade vetorial instantânea pode ser definida pelo quanto foi deslocado vetorialmente em um intervalo de tempo infinitesimal, chegando próximo a zero. Ela pode ser calculada pela fórmula:
\(\vec{v}_{inst}=\frac{∆\vec{x}}{∆t}\)
-
\(\vec{v}_{inst}\) é a velocidade vetorial instantânea, medida em \([m/s] \).
-
\(∆\vec{x}\) é a variação de deslocamento vetorial, medida em metros \([m] \).
-
\(∆t \) é a variação de tempo, medida em segundos \([s]\).
No entanto, a fórmula verdadeira utilizada para o cálculo da velocidade instantânea é escrita em termos de um limite em que o intervalo de tempo tende a zero, ou de derivada (estudada nos cursos superiores que possuem a disciplina de Física), conforme podemos ver abaixo:
\(v_{inst}=\stackrel{lim}{\tiny∆t→0}\frac{∆x}{∆t}=\frac{dx}{dt}\)
-
\(v_{inst}\) é a velocidade instantânea, medida em \( [m/s] \).
-
\(\stackrel{lim}{\tiny∆t→0}\) é o limite em que a variação do tempo tende a zero.
-
\(∆x \) é a variação de deslocamento, medida em metros \( [m] \).
-
\(∆t \) é a variação de tempo, medida em segundos \([s]\).
-
\(\frac{dx}{dt}\) é a derivada em relação ao tempo do deslocamento.
Leia também: Cálculo do deslocamento por meio do gráfico da velocidade
Exercícios resolvidos sobre velocidade vetorial
Questão 1
(PUC-SP) Se a velocidade vetorial de um ponto material é constante e não nula, sua trajetória
a) é uma parábola.
b) pode ser retilínea, mas não necessariamente.
c) deve ser retilínea.
d) é uma circunferência.
e) pode ser uma curva qualquer.
Resolução:
Alternativa C. A trajetória será retilínea quando a velocidade vetorial for não nula e constante, em que sua orientação e módulo também serão constantes.
Questão 2
(Fatec) Um automóvel percorre 6,0 km para o norte e, em seguida, 8,0 km para o leste. A intensidade do vetor posição, em relação ao ponto de partida, é:
a) 10 km
b) 14 km
c) 2,0 km
d) 12 km
e) 8,0 km
Resolução:
Alternativa A. Primeiramente é necessário compreender o percurso feito pelo carro, conforme demonstrado na imagem abaixo:
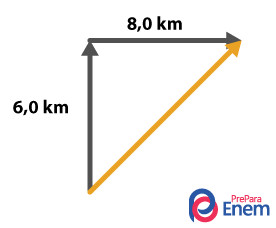
O vetor amarelo se trata do vetor posição. Para encontrar sua intensidade, precisamos utilizar a fórmula de Pitágoras, em que a hipotenusa é o vetor posição:
\(hipotenusa^2=cateto^2+cateto^2\)
\(∆\vec{x}^2=\vec{x}_o^2+\vec{x}^2\)
\(∆\vec{x}^2=6^2+8^2\)
\(∆\vec{x}^2=36+64\)
\(∆\vec{x}^2=100\)
\(∆\vec{x}=\sqrt{100}\)
\(∆\vec{x}=10\ km\)