Velocidade de escape

Velocidade de escape é a menor velocidade necessária para que um corpo consiga escapar da atração exercida pela gravidade de algum corpo celeste, como a Terra, a Lua, ou qualquer outro planeta, sem o auxílio de uma propulsão no ar (como no caso dos foguetes). Desconsiderando-se a ação da resistência do ar, a velocidade de escape da Terra é de cerca de 11,2 km/s, aproximadamente 40.000 km/h.

Veja também: Exoplanetas – o que são, onde ficam e quantos conhecemos?

Tópicos deste artigo

• 1 - Fórmula da velocidade de escape
• 2 - Velocidade de escape de outros planetas
• 3 - Exercícios sobre velocidade de escape

Fórmula da velocidade de escape

A fórmula da velocidade de escape é obtida considerando-se que a energia cinética de um corpo que é lançado da superfície da Terra transforme-se integralmente em energia potencial gravitacional.

De acordo com a lei da gravitação universal, de Isaac Newton, a gravidade de um objeto de formato circular, que é uma boa aproximação para o formato de estrelas e planetas, de massa M e raio R, pode ser calculada da seguinte forma:

G – constante da gravitação universal (6,67.10^-11 m³ kg^-1s^-2)
M – massa do corpo (kg)
R – raio do corpo (m)

Dessa forma, se um corpo é lançado da superfície da Terra, ao nível do mar, com uma velocidade v, e toda sua energia cinética transforma-se em energia potencial gravitacional, é possível obtermos a seguinte expressão para a velocidade de escape, observe:

Como é possível ver no resultado obtido, a velocidade de escape não depende da massa do objeto, mas somente da massa do planeta (M).

Velocidade de escape de outros planetas

Na tabela a seguir, é possível observar os valores das velocidades de escape de outros planetas, do Sol e também da Lua, partindo de suas superfícies, confira:

Outra velocidade de escape interessante de se conhecer é a do Sol, partindo dos planetas do Sistema Solar. Partindo-se da Terra, para escaparmos completamente da atração gravitacional do Sol, é necessária uma velocidade de 42,1 km/s, mais de 150.000 km/h!

Exercícios sobre velocidade de escape

Questão 1) Determinado planeta apresenta velocidade de escape v, massa m e raio r. Um outro planeta, cuja massa é quatro vezes maior e que tem o mesmo raio, deverá apresentar uma velocidade de escape v', tal que:

a) v' = v/2
b) v' = 2v
c) v' = 4v
d) v' = v/4
e) v' = v/16

Gabarito: Letra B

Resolução:

Para resolver o exercício, usaremos a fórmula da velocidade de escape e chamaremos a velocidade de escape do segundo planeta de v'. Em seguida, utilizaremos o valor de 4M no lugar da massa do primeiro planeta, que é somente M. Por fim, basta tirarmos esse valor de dentro da raiz quadrada e, assim, obtermos a seguinte relação:

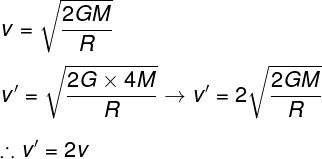
Questão 2) Desprezando-se a resistência do ar, um objeto de massa m, e que se move em uma velocidade maior que 11,2 km/s, pode ser lançado para fora da Terra. Se desejarmos lançar um objeto de massa 2m para fora da Terra, sob condições idênticas às quais o objeto de massa m fora lançado, a mínima velocidade de escape será de:

a) 22,4 km/s
b) 5,6 km/s
c) 3,4 km/s
d) 11,2 km/s
e) 4,8 km/s

Gabarito: Letra D

Resolução:

A velocidade de escape da Terra depende de somente de três coisas: da constante da gravitação universal, da massa da Terra e da distância de onde o objeto se encontra até o centro da Terra, portanto, mesmo que se lance objetos de diferentes massas, a velocidade de escape da Terra continua igual para todos.