O termo trabalho é muito utilizado no nosso cotidiano para definir o desempenho de qualquer atividade ou tarefa, independentemente da forma como elas são realizadas. A palavra “trabalho” pode fazer referência tanto a uma pessoa que exerce suas atividades em um escritório e não se movimenta muito durante o dia quanto à outra pessoa que passa o dia todo em uma obra, carregando peso e sempre em movimento.
No entanto, a definição física de trabalho é diferente da que utilizamos no dia a dia. De acordo com a Física, só existe trabalho se houver um deslocamento de um determinado corpo pela aplicação de uma força. Como podemos encontrar a relação do trabalho com outras grandezas, utilizamos o termo trabalho mecânico para estudar a relação entre a força e o deslocamento de um corpo.
O trabalho mecânico é definido como a relação entre a força (F) aplicada sobre um corpo e o deslocamento (d) sofrido por ele. Matematicamente, essa relação é dada pela expressão:
T = F . d. Cos α
*α é o ângulo entre a força e o deslocamento.
A partir dessa equação, podemos inferir que, quanto maior a força e o deslocamento de um corpo, maior será o trabalho mecânico.
A unidade de medida do trabalho mecânico no Sistema Internacional é N.m, pois a unidade de medida da força é o Newton (N) e a do deslocamento é o metro (m). O produto N . m é também conhecido como Joule — simbolizado pela letra J — em homenagem a James Prescott Joule. A definição física para o Joule é a seguinte: o trabalho realizado por uma força de 1 Newton que é exercida na mesma direção e sentido do deslocamento de 1 m.
Cálculo do trabalho mecânico
A definição matemática dada anteriormente é a forma básica de fazer o cálculo do trabalho mecânico realizado sobre um corpo. Todavia, devemos fazer a análise considerando a direção e o sentido da força e do deslocamento do corpo.
-
Trabalho realizado por uma força constante
Quando a força aplicada sobre o corpo é constante, devemos considerar três situações:
-
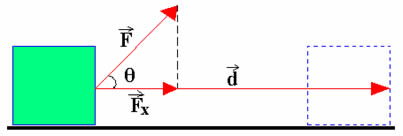
O ângulo α está entre zero e noventa graus (0º ≤ α < 90º), conforme mostra a figura:

Diagrama demonstrando o sentido e a direção da força e do deslocamento de um corpo com 0º ≤ α < 90º
Quando o ângulo entre a força e o deslocamento do corpo está entre 0º e 90º, o trabalho é positivo, pois os cossenos dos ângulos nesse intervalo sempre assumem valores positivos. Além disso, a força e o deslocamento estão na mesma direção, portanto, como apresentam sinais iguais, o produto entre eles é positivo.
-
Quando α = 90º:

Diagrama demonstrando o sentido e a direção da força e do deslocamento de um corpo com α = 90º
Quando α = 90º, o trabalho é nulo, pois, ao substituirmos 90º na equação anterior, teremos:
T = F . d. Cos 90
Como o cosseno de 90º é zero, o resultado da equação anterior também é zero.
-
O último caso a ser analisado para o trabalho realizado por uma força é quando o ângulo α é maior que 90º e menor que 180º (90º < α < 180º). Observe a figura:

Diagrama demonstrando o sentido e a direção da força e do deslocamento de um corpo com 90º < α < 180º
Nesse caso, o trabalho assume valor negativo, já que a força e o deslocamento estão em sentidos opostos, o que significa que a força é exercida no sentido oposto ao deslocamento.
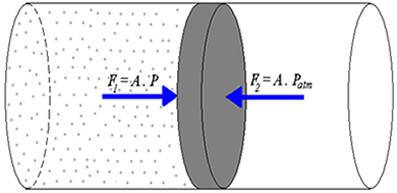
Neste texto, fizemos a análise do trabalho mecânico realizado apenas por uma força constante, mas o trabalho também pode ser realizado por uma força variável. Para saber mais sobre o assunto, leia o texto “Trabalho de uma força variável”. Além disso, é válido ressaltar que o trabalho mecânico também pode ser realizado por um gás, mas como esse assunto não era o foco deste texto, confira o esse conteúdo através do texto“Trabalho a pressão constante”. Não deixe de conferir também a relação entre trabalho e energia!
Aproveite para conferir a nossa videoaula relacionada ao assunto: