Quando falamos em trabalho geralmente nos vem à mente algo relacionado a esforço físico, pois associamos trabalho a esforço, como mover uma mesa, cortar grama, lavar louças etc. Mas na Física a definição de trabalho é diferente, relacionamos trabalho ao deslocamento ou à deformação de uma força. Sendo assim, trabalho é o produto de uma força pelo deslocamento. Matematicamente, temos:
τ=F.d
A equação acima nos permite calcular o trabalho de uma força aplicada na direção horizontal, agora se essa força for aplicada a um corpo obliquamente, passa a ser usada a decomposição vetorial na equação, que é reescrita da seguinte forma:
τ=F.d.cos?θ
Onde θ (teta) é o ângulo formado entre o vetor força e a direção horizontal.
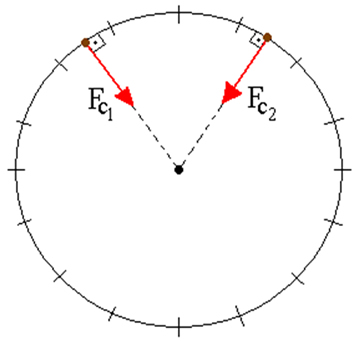
Vejamos a figura acima. De acordo com a ilustração podemos dizer que o corpo se encontra em movimento circular. No movimento circular, a força resultante que age sobre o corpo é a força centrípeta, portanto, para determinarmos o trabalho realizado pela força centrípeta temos que fazer uma divisão da circunferência em pequenos pedaços e calcular o trabalho em cada pedaço da divisão.
Ao fazer a divisão perceberemos que para cada pedaço pequeno a força centrípeta é perpendicular ao deslocamento, portanto, o trabalho em cada pedaço é nulo. Podemos concluir que o trabalho de uma força centrípeta é sempre nulo.
Vejamos pela matemática:
Como a força centrípeta é sempre perpendicular ao deslocamento, temos que o ângulo entre a força e o deslocamento vale θ = 90º. Apliquemos a equação:
τ=F.d.cos?θ
Como o cos θ = 90º, temos:
τ=F.d.cos?90°
Mas o cos 90º = 0, temos que:
τ=F.d.0 ? τ=0
Aproveite para conferir as nossas videoaulas relacionadas ao assunto: