O torque é o principal agente da rotação, produzido sempre que aplicamos uma força sobre um braço de alavanca, de modo que quanto quanto mais distante for o braço de alavanca de um objeto, maior é a facilidade em rotacioná-lo. Se não há movimento rotacional, o torque está equilibrado, se tratando do equilíbrio de rotação.
Acesse também: Mecânica no Enem — como esse tema é cobrado?
Tópicos deste artigo
- 1 - Resumo sobre torque
- 2 - Videoaula sobre torque
- 3 - O que é o torque?
- 4 - Fórmulas do torque
- 5 - Como calcular o torque?
- 6 - Equilíbrio de rotação
- 7 - Torque e momento angular
- 8 - Exemplos de torque
- 9 - Exercícios resolvidos sobre torque
Resumo sobre torque
-
Para rotacionarmos um objeto, é necessária a aplicação do torque, que é uma grandeza física vetorial.
-
A direção e sentido do torque são determinados pela regra da mão direita.
-
Movimentos no sentido horário têm torque negativo, já movimentos no sentido anti-horário têm torque positivo.
-
Calculamos o torque por meio do produto entre a força aplicada, a distância do eixo e o seno do ângulo formado entre eles.
-
A unidade do torque é Newton por metro.
-
No equilíbrio de rotação, a soma dos torques é nula, e o momento angular é constante.
-
Momento angular é o produto entre o raio, o momento linear e o seno do ângulo entre eles.
Videoaula sobre torque
O que é o torque?
Torque é uma grandeza física vetorial que pode ser definida como o agente dinâmico da rotação. Ou seja, para haver movimento rotacional, é indispensável a aplicação de torque, similarmente ao movimento translacional, para o qual é necessária a utilização de uma força.
Ele está relacionado à aplicação de uma força sobre o braço de alavanca (distância até o eixo de rotação, compreendido como o ponto que gira do objeto). Quanto mais distante for o braço de alavanca de um objeto, maior será a facilidade em rotacioná-lo, conforme podemos ver na imagem.
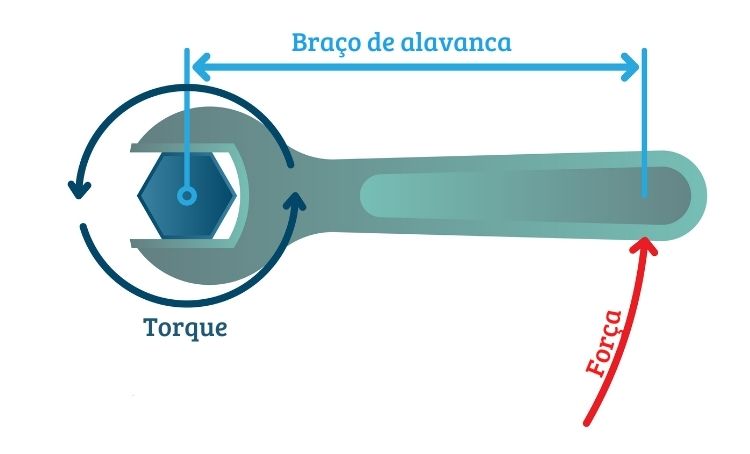
Por ser uma grandeza vetorial, o torque possui direção, sentido e módulo:
-
Direção e sentido: determinados pela regra da mão direita. Fechamos a mão em direção à força, e o dedão que está perpendicular à mão corresponde ao torque.
-
Módulo: determinado por meio do cálculo. Seu sinal por ser positivo quando o movimento for no sentido anti-horário ou negativo quando o movimento for no sentido horário
→ Unidade de torque
A unidade de medida do torque, de acordo com o Sistema Internacional de Unidades (SI), é Newton por metro, representado por \(N\bullet m.\).
Fórmulas do torque
→ Cálculo do torque vetorialmente
\(\vec{\tau}=\vec{r}·F\)
-
\(\vec{\tau}\) → vetor torque
-
\(\vec{r}\) → vetor posição
-
\(\vec{F}\) → vetor força aplicada
→ Módulo do torque
\(\tau=r\bullet F\bullet\sin{\theta}\)
-
\(\tau\) → torque produzido, medido em \([N\bullet m]\).
-
\(r\) → distância do eixo de rotação, também chamado de braço de alavanca, medida em metros \([m]\).
-
\(F\) → força produzida, medida em Newton \([N].\).
-
\(\theta\) → ângulo entre a distância e a força, medido em graus [°].
Como calcular o torque?
Podemos calcular o torque por meio da multiplicação da distância pela força e pelo seno do ângulo entre elas.
-
Exemplo 1:
Uma força de 400 N é aplicada perpendicularmente ao plano de uma porta, em uma distância de 100 cm do eixo de rotação dessa porta, que passa a girar no sentido anti-horário. O torque produzido por essa força é igual a:
Resolução:
Encontraremos o torque produzido utilizando a fórmula:
\(\tau=r\bullet F\bullet\sin{\theta}\)
Contudo, primeiramente devemos converter a distância de centímetros para metros, sendo que 100 cm = 1 m.
Além disso, como a força é aplicada perpendicularmente ao eixo, ou seja, fazendo um ângulo de \(90°\), então \( \theta=90°\):
\(\tau=1\bullet400\bullet\sin90°\)
\(\tau=1\bullet400\bullet1\)
\(\tau=400\ N\bullet m\)
O torque vale \(400\ N\bullet m\), com sinal positivo, já que a porta gira no sentido anti-horário.
-
Exemplo 2:
Uma maçaneta circular, cujo eixo de rotação encontra-se em seu centro, tem diâmetro de 2 cm e é girada no sentido horário por uma força de 25 N. Determine o torque aplicado sobre a maçaneta.
Resolução:
Encontraremos o torque produzido usando a sua fórmula:
\(\tau=r\bullet F\bullet\sin{\theta}\)
Converteremos a distância de centímetros para metros, sendo que \(2\ cm=0,02\ m\).
\(\tau=0,02\bullet25\bullet\sin90°\)
\(\tau=0,02\bullet25\bullet1\)
\(\tau=-\ 0,5\ N\bullet m\)
O torque vale \(-\ 0,5\ N\bullet m\), com sinal negativo, já que a maçaneta gira no sentido horário.
Equilíbrio de rotação
O equilíbrio de rotação ocorre quando a soma vetorial de todos os momentos de torque geram um resultado nulo, fazendo com que o objeto não rotacione ou gire com uma velocidade angular constante e, consequentemente, aceleração angular nula.
Torque e momento angular
Momento angular surge sempre que há corpos em rotação. Como o torque é o responsável pela rotação, existe uma relação proporcional entre eles, sendo que quanto maior é o momento angular, maior é o torque, representado pela fórmula:
\(\tau=\frac{∆L}{∆t}\)
-
\(\tau \) → torque, medido em \( [N\bullet m]\).
-
\(∆L\) → variação do momento angular, medida em \(\left[{kg\bullet m^2}{s}\right]\).
-
\(∆t\) → variação de tempo, medida em segundos \([s]\).
Importante: Vale resaltar que se trabalhamos com um caso em que há equilíbrio de rotação, como o somatório dos torques é nulo, seu momento angular permanece constante.
O momento angular pode ser calculado de duas maneiras distintas. Assim como no caso do torque, uma das formas é vetorialmente e a outra forma é considerando seu módulo:
\(\vec{L}=\vec{r}\bullet\vec{p}\)
\(L=r\bullet p\bullet\sin{\theta}\)
-
\(\vec{L}\) → vetor momento angular
-
\(\vec{r}\) → vetor posição
-
\(\vec{p} \) → vetor momento linear
-
\(L\) → momento angular, medido em \(\left[{kg\bullet m^2}{s}\right]\).
-
\(r\) → distância entre o objeto e o eixo de rotação ou raio, medida em metros \([m]\).
-
\(p\) → momento linear, medido em \(\left[{kg\bullet m}{s}\right]\).
-
\(\theta\) → ângulo entre \(r\) e \(Q\), medido em graus [°].
Já o momento linear pode ser calculado pela fórmula:
\(p=m\bullet v\)
-
p → momento, medido em \(\left[{kg\bullet m}{s}\right]\).
-
m → massa, medida em quilogramas \( [kg]\).
-
v → velocidade, medida em metros por segundo \( \left[{m}/{s}\right]\).
Saiba mais: Física do Hand Spinner
Exemplos de torque
Existem diversos exemplos de casos em que o torque é empregado, com o intuito de aproveitá-lo ao máximo fazendo o mínimo esforço na sua utilização, como no uso de chaves de fenda, chaves de torção, braçadeiras de portas, maçanetas, alavancas, entre outros.
Por exemplo, a maçaneta é colocada o mais distante possível da braçadeira da porta, para que possamos abri-la com o mínimo de esforço. Além disso, para abrirmos a porta, precisamos aplicar torque na maçaneta.
Exercícios resolvidos sobre torque
Questão 1
(Udesc) Ao fechar uma porta, aplica-se uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças. Com relação ao movimento dessa porta, analise as proposições.
I. Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, menos efetivo é o torque da força.
II. A unidade do torque da força no SI é N·m, podendo também ser medida em Joule (J).
III. O torque da força depende da distância perpendicular entre a maçaneta e as dobradiças.
IV. Qualquer que seja a direção da força, o seu torque será não nulo. Consequentemente, a porta rotacionará sempre.
Assinale a alternativa correta.
A) Somente a afirmativa II é verdadeira.
B) Somente as afirmativas I e II são verdadeiras.
C) Somente a afirmativa IV é verdadeira.
D) Somente a afirmativa III é verdadeira.
E) Somente as afirmativas II e III são verdadeiras.
Resolução:
Alternativa D
I. Falsa
Quanto maior a distância perpendicular entre a maçaneta e as dobradiças, mais efetivo é o torque da força.
II. Falsa
A unidade do torque da força no SI é N·m, mas o torque não pode ser medido em Joule (J), que é uma unidade de medida de energia.
III. Verdadeira
O torque da força depende, de fato, da distância perpendicular entre a maçaneta e as dobradiças.
IV. Falsa
Nem sempre teremos torque, como no caso de a força ser paralela ao eixo de rotação.
Questão 2
Uma maçaneta circular que está a uma distância de 10 cm do seu eixo de rotação é girada no sentido horário durante 5 segundos. Supondo que o momento linear vale \(45\ {kg\bullet m}{s}\), determine o torque aplicado sobre a maçaneta.
A) \(-\ 0,9\ N·m\)
B) \(+\ 0,9\ N·m\)
C) \(– 90\ N·m\)
D) \(+\ 90\ N·m\)
E) \(– 900\ N·m\)
Resolução:
Alternativa A
Descobrindo o momento angular, conseguiremos determinar o torque produzido:
\(L=r\bullet p\bullet\sin{\theta}\)
Convertendo a distância de centímetro para metro e considerando que a força aplicada é perpendicular ao eixo, fazendo um ângulo de 90°, então \(\theta=90°\):
\(L=0,1\bullet45\bullet\sin90°\)
\(L=0,1\bullet45\bullet1\)
\(L=4,5\ {kg\bullet m^2}{s}\ \)
O torque produzido durante os 5 segundos foi de:
\(\tau=\frac{L}{t}\)
\(\tau=\frac{4,5}{5}\)
\(\tau=-\ 0,9\ N\bullet m\)
O torque vale \(-\ 0,9\ N\bullet m\). Seu sinal é negativo para indicar que o sentido do movimento da maçaneta é horário.