Resistividade

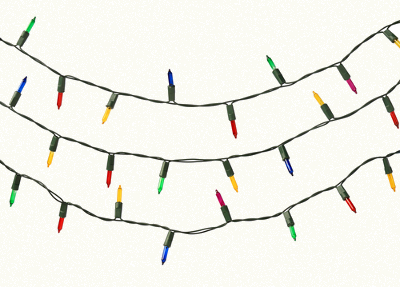
A resistividade é uma propriedade da matéria relacionada à oposição à quantidade de corrente elétrica que a percorre. Isso implica que, quanto maior a resistividade de uma substância, maior será a dificuldade da corrente elétrica para percorrê-la. Dessa forma, se a resistividade for muito elevada, têm-se uma substância isolante, como no caso da fita isolante demonstrada na figura anterior.

O oposto da resistividade é a condutividade da substância, e, por sua vez, quanto maior ela for, menor será a resistividade, consequentemente, caracterizando a substância como condutora.

A resistividade está diretamente relacionada com a resistência elétrica e, assim, com as leis de Ohm. Cada substância possui um valor específico da resistividade, logo, seu valor está relacionado ao elemento da matéria e à temperatura do elemento quando está sendo percorrido por corrente elétrica.

Leia também: Rigidez dielétrica — a tensão máxima suportada pelo material isolante

Tópicos deste artigo

• 1 - Resumo sobre resistividade elétrica
• 2 - O que é resistividade elétrica?
• 3 - Quais são os fatores que influenciam na resistividade elétrica?
• 4 - Quais são as fórmulas da resistividade elétrica?
  • Exemplos
• 5 - Unidade de medida da resistividade elétrica
• 6 - Resistividade dos materiais
• 7 - Resistividade elétrica x condutividade
• 8 - Resistividade elétrica x resistência elétrica
• 9 - Exercícios resolvidos sobre resistividade elétrica

Resumo sobre resistividade elétrica

• A resistividade é uma propriedade da matéria que determina sua oposição à passagem de corrente elétrica.
• A resistividade é influenciada pelo elemento que compõe a matéria e por sua temperatura.
• Quando a resistividade de uma substância é muito elevada, a substância é um isolante.
• Quando a resistividade de uma substância é muito baixa, a substância é um condutor.
• A propriedade oposta à resistividade é a condutividade.
• Quanto maior a resistividade, maior será a resistência elétrica de um circuito.

O que é resistividade elétrica?

A resistividade elétrica é a propriedade da matéria de resistir ao fluxo da corrente elétrica. Sendo assim, cada elemento da Tabela Periódica, ou a combinação deles, apresenta um valor para sua resistividade. Expressando seu significado de uma forma visual, a resistividade seria o conjunto de empecilhos para a corrente elétrica contidos dentro de todos os elementos, em que a quantidade deles por comprimento variaria de um elemento para outro.

Quanto maior o valor da resistividade de uma substância, menor será o fluxo da corrente que a percorre. Desse modo, corpos com resistividade elétrica muito elevada são considerados isolantes e aqueles com resistividade muito baixa são considerados condutores.

Quais são os fatores que influenciam na resistividade elétrica?

A resistividade elétrica é influenciada pela composição do corpo, em que, geralmente, os metais apresentam valores muito baixos, já que os metais conduzem corrente elétrica. Por sua vez, os ametais apresentam valores de resistividade elétrica mais elevados, já que não conduzem corrente elétrica.

Outro fator que influencia na resistividade é a temperatura. Quanto mais elevada a temperatura do corpo, mais seus átomos vibrarão, consequentemente, isso dificultará mais ainda o fluxo da corrente elétrica, e, devido a isso, sua resistividade aumenta. Isso está relacionado com o efeito Joule da corrente elétrica, já que, quanto mais um condutor aquece, mais corrente ele consumirá para se manter funcionando. Isso é porque a energia elétrica é dissipada na forma de energia térmica (calor).

Quais são as fórmulas da resistividade elétrica?

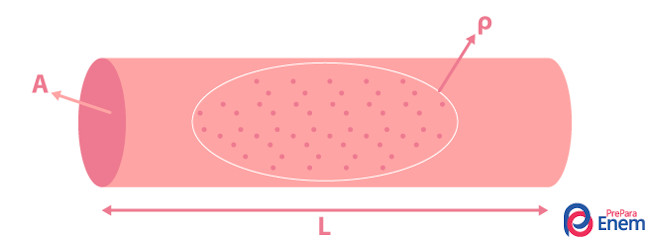
A resistividade elétrica está associada à segunda lei de Ohm. Esta afirma que a resistência elétrica de um condutor é proporcional à sua resistividade e ao seu comprimento e inversamente proporcional à sua área transversal (onde ocorre a entrada da corrente no condutor).

\(R=\frac{\rho\cdot L}{A}\ (segunda\ lei\ de\ Ohm)\)

Isolando a resistividade nessa equação, tem-se:

\(\rho=\frac{R\cdot A}{L}\)

• ρ = resistividade elétrica (Ω·m);
• R = resistência elétrica (Ω);
• L = comprimento do condutor (m);
• A = área transversal do condutor (m²).

Como a resistividade está diretamente relacionada com a temperatura do condutor, a fórmula a seguir demonstra tal relação.

\(\rho=\rho_0\cdot(1+\alpha\cdot∆T)\)

\(∆T=T-T_0\)

• ρ₀ = resistividade elétrica inicial, ou seja, antes da variação da temperatura (Ω·m);
• ρ = resistividade após a variação da temperatura (Ω·m);
• ΔT = variação da temperatura (°C);
• α = coeficiente de dilatação linear do condutor (°C^-1);
• T = temperatura final (°C);
• T₀ = temperatura inicial (°C).

Pela fórmula, é possível perceber que, quanto maior a variação de temperatura, maior será a nova resistividade.

• Exemplos

1. Qual é a resistência elétrica de um condutor de 3 m de comprimento, área transversal de 1,2·10^-4 m² e resistividade elétrica valendo 2·10^-7 Ω·m?

Extraindo os dados do problema:

• R = ?
• L = 3 m
• A = 1,2·10^-4 m²
• ρ = 2·10^-7 Ω·m

\(R=\frac{\rho\cdot L}{A}=\frac{{2\cdot10}^{-7}\cdot3}{{1,2\cdot10}^{-4}}=\frac{{6\cdot10}^{-7}}{{1,2\cdot10}^{-4}}={5\cdot10}^{-7-(-4)}={5\cdot10}^{-3}\Omega\)

2. Um condutor de resistividade igual a 5·10^-6 Ω·m, enquanto é percorrido por corrente elétrica, tem sua temperatura variando de 25 °C para 65 °C. Sabendo que seu coeficiente de dilatação linear é de, aproximadamente, 0,004°C^-1, determine o valor da resistividade após a variação da temperatura do condutor.

Extraindo os dados do problema:

• ρ = 5·10^-6 Ω·m
• T₀ = 25 °C
• T = 65 °C
• α = 0,004 °C^-1
• ρ = ?

Calcula-se primeiro a variação de temperatura:

\(∆T=T-T_0=65-25=40 °C\)

\(\rho=\rho_0\cdot(1+α\cdot∆T)=5\cdot10^{-6}\cdot(1+0,004\cdot40)=5\cdot10^{-6}\cdot(1+0,16)\)

\(\rho={5\cdot10}^{-6}\cdot\left(1,16\right)={5,8\cdot10}^{-6}\ \Omega·m\)

Leia também: As principais equações utilizadas no estudo da eletricidade

Unidade de medida da resistividade elétrica

A resistividade elétrica é medida em ohm por metro (Ω·m). Essa unidade implica a resistência do corpo por unidade do seu comprimento em metros, o que significa que, quanto maior o comprimento do condutor, maior será sua resistência elétrica.

Resistividade dos materiais

A resistividade elétrica dos materiais está relacionada a sua composição. No caso dos metais ou ligas metálicas, seu valor terá a ordem de grandeza em torno de 10^-8. No caso dos semicondutores, a ordem de grandeza será entre de 10^-5 e 10², e, para os isolantes, ela será acima de 10².

Associando isso à Tabela Periódica, os elementos das famílias 1A, 2A, 3A e família B terão resistividade baixa; para elementos da família 5A a 7A, em sua grande maioria, haverá resistividade elevada, já que se trata dos ametais, ou seja, isolantes. A tabela a seguir demonstrará a resistividade de alguns materiais.

Resistividade elétrica x condutividade

A resistividade é uma propriedade associada ao impedimento do fluxo de corrente elétrica no condutor, e, quanto maior o valor da resistividade, menor será o fluxo da corrente elétrica. A condutividade exerce propriedade inversa à da resistividade, portanto, quanto maior o seu valor, maior será o fluxo da corrente elétrica no material. Ela é representa pela letra grega σ (sigma), e sua unidade de medida é o ohm por metro a menos um (Ω·m)^-1.

\(\sigma=\frac{1}{\rho}\)

Resistividade elétrica x resistência elétrica

Como foi mencionado acima, a resistividade elétrica está diretamente relacionada à resistência elétrica, ou seja, quanto maior a resistividade do material, maior será a resistência elétrica do condutor formado por ele. A resistividade é introduzida na segunda lei de Ohm, que relaciona a resistência do condutor com sua composição, comprimento e área transversal, como é descrito na equação da segunda lei de Ohm.

\(R=\frac{\rho\cdot L}{A}\)

Leia também: Tensão elétrica — resultante do movimento de uma carga na presença de um campo elétrico

Exercícios resolvidos sobre resistividade elétrica

Questão 1

Um condutor de 8 metros de comprimento possui resistência elétrica e área transversal, respectivamente, iguais a 9·10^-5 Ω e 1,6·10^-3 m². Marque a alternativa que representa a resistividade da substância que compõe esse condutor.

a) 5∙10-⁸Ω∙m

b) 7∙10^-8Ω∙m  

c) 1,8∙10^-8Ω∙m

d) 4,6∙10^-8Ω∙m

e) 8∙10^-8Ω∙m

Resposta: letra C

Extraindo os dados:

• L = 8 m
• R = 9·10^-5 Ω
• A = 1,6·10^-3 m²
• ρ = ?

Utiliza-se a variação da 2ª lei de Ohm.

\(\rho=\frac{R\cdot A}{L}=\frac{{9\cdot10}^{-5}\cdot{1,6\cdot10}^{-3}}{8}=\frac{14,4\cdot{10}^{-8}}{8}={1,8\cdot10}^{-8}\Omega\)

Questão 2

Em um laboratório, foram construídos três cilindros (A, B e C), com exatamente as mesmas dimensões. Os três foram ligados na mesma tensão elétrica, com isso, foi medida a corrente em cada um com um amperímetro, e os valores obtidos foram iguais a:

• A → 8 mA
• B → 0,5 mA
• C → 6 mA

Marque a alternativa correta:

a) A resistividade do cilindro A é maior que as dos demais.

b) A condutividade do cilindro B é a menor dos três.

c) A condutividade de C é maior do que a condutividade de A.

d) A resistividade de B é menor que a resistividade de C.

e) Todos possuem o mesmo valor de resistividade, já que ela não se relaciona em nada com o fluxo da corrente no condutor.

Resposta: letra B

Comparando as três correntes:

A > C > B

Quanto maior a corrente, maior será a condutividade elétrica, dessa forma, a relação será a mesma que a da corrente. Por sua vez, o comportamento da corrente é oposto ao da resistividade, comparando a resistividade de cada um dos cilindros.

B > C > A

a) A resistividade do cilindro A é maior que a dos demais. (Falsa)

b) (Verdadeira)

c) A condutividade de C é menor do que a condutividade de A. (Falsa)

d) A resistividade de B é maior que a resistividade de C. (Falsa)

e) A resistividade se relaciona diretamente com o fluxo da corrente no condutor. (Falsa)