Resistência elétrica

A resistência elétrica é uma propriedade física existente nos resistores cuja principal função é de se opor à trasmissão de corrente elétrica no circuito elétrico. É uma grandeza física escalar que converte energia elétrica em energia térmica e evita a passagem de corrente elétrica pelo circuito elétrico. Ela é calculada através da primeira e segunda lei de Ohm.

Leia também: O que é a condutividade elétrica?

Tópicos deste artigo

• 1 - Resumo sobre resistência elétrica
• 2 - O que é resistência elétrica?
• 3 - Qual a função da resistência elétrica?
• 4 - Quais são as fórmulas da resistência elétrica?
  • → Primeira lei de Ohm
  • → Segunda lei de Ohm
• 5 - Como se calcula a resistência elétrica?
• 6 - Fatores que influenciam na resistência elétrica
• 7 - Resistência elétrica x resistividade elétrica
• 8 - Efeito Joule
• 9 - Exercícios resolvidos sobre resistência elétrica

Resumo sobre resistência elétrica

• A resistência elétrica é uma propriedade física existente nos resistores cuja principal função é de se opor à trasmissão de corrente elétrica no circuito elétrico.

• A resistência elétrica é capaz de resistir à corrente elétrica devido à colisão entre os átomos do condutor e os elétrons livres da corrente elétrica.

• Através das fórmulas da primeira e segunda lei de Ohm podemos calcular a resistência elétrica.

• A resistividade elétrica e o comprimento do condutor são diretamente proporcionais à resistência elétrica.

• A área de secção transversal do condutor é inversamente proporcional à resistência elétrica.

• Devido ao efeito Joule, a energia elétrica pode ser convertida em calor.

O que é resistência elétrica?

A resistência elétrica é uma propriedade física dos resistores, um componente eletrônico representado como um zigue-zague ou um quadrado nos circuitos elétricos, como demonstrado na imagem abaixo:

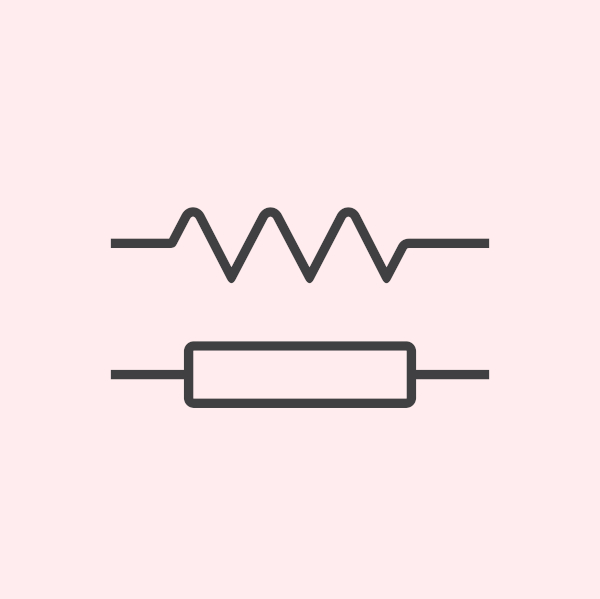
A unidade de medida da resistência elétrica pelo Sistema Internacional de Unidades (S.I.) é Ohm, representada pela letra grega ômega (Ω).

Qual a função da resistência elétrica?

A função da resistência elétrica é impedir o fluxo da corrente elétrica pelo circuito elétrico e transformar a energia elétrica recebida em calor. Ela é capaz de fazer isso porque quando um condutor elétrico é conectado a uma tensão elétrica, ele passa a ser percorrido por um fluxo de elétrons livres, que compõem a corrente elétrica e colidem com os átomos do condutor, dificultando o fluxo da corrente elétrica. Dessa forma, quanto mais colisões tivermos, mais dificuldade a corrente elétrica terá em atravessar o condutor.

Quais são as fórmulas da resistência elétrica?

→ Primeira lei de Ohm

\(R = \frac{U}{i} \)

• U → diferença de potencial elétrico (ddp), medida em Volts [V].

• R → resistência elétrica, medida em Ohm [Ω].

• i → corrente elétrica, medida em Ampére [A].

→ Segunda lei de Ohm

\(\rho = \frac{R \cdot A}{L} \)

• ρ → resistividade elétrica e do material, medida em Ohm-metro [Ω∙m].

• R → resistência elétrica, medida em Ohm [Ω].

• L → comprimento do condutor, medido em metros [m].

• A → a área de secção transversal do condutor, medida em metros quadrados [m²].

Como se calcula a resistência elétrica?

A resistência elétrica pode ser calculada através das fórmulas da primeira ou da segunda lei de Ohm, dependendo das informações fornecidas pelo enunciado.

• Exemplo 1:

Calcule a resistência elétrica de um resistor que é percorrido por uma corrente elétrica de \(5 \cdot 10^{-3} \, \text{A} \) quando associado a uma ddp de 110 V.

Resolução:

Calcularemos a resistência elétrica através da fórmula da primeira lei de Ohm:

\(R = \frac{U}{i} \)

\(R = \frac{110}{5 \cdot 10^{-3}} \)

\(R = 22 \cdot 10^3 \)

\(2,2 \cdot 10^4 \, \Omega \)

A resistência elétrica desse resistor é de \(2,2 \cdot 10^4 \, \Omega \).

• Exemplo 2:

Calcule a resistência elétrica de um fio de 3,5 metros de comprimento e área de secção transversal de 0,1 metro quadrado, sabendo que a sua resistividade elétrica é de \(2 \cdot 10^{-6} \, \Omega \cdot m \).

Resolução:

Calcularemos a resistência elétrica através da fórmula da segunda lei de Ohm:

\(R = \frac{\rho \cdot L}{A} \)

\(R = 2 \cdot 10^{-6} \cdot \frac{3,5}{0,1} \)

\(R = 70 \cdot 10^{-6} \)

\(R = 7 \cdot 10^{-5} \, \Omega \)

A resistência elétrica desse fio é de \(7\cdot {10} ^ {-5 } Ω \).

Fatores que influenciam na resistência elétrica

Os fatores que mais influenciam na resistência elétrica são a resistividade elétrica e as proporcões (área de secção transversal e comprimento) do condutor.

• Resistividade elétrica: a resistividade elétrica do condutor é diretamente proporcional à resistência elétrica. À medida que a resistividade elétrica aumenta, a resistência elétrica também aumenta.

• Área de secção transversal: a área de secção transversal do condutor é inversamente proporcional à resistência elétrica. À medida que a área de secção transversal aumenta, a resistência elétrica diminui.

• Comprimento: o comprimento do condutor é diretamente proporcional à resistência elétrica. À medida que o comprimento aumenta, a resistência elétrica aumenta.

Resistência elétrica x resistividade elétrica

A resistência elétrica e a resistividade elétrica são grandezas físicas escalares diretamente proporcionais e associadas à oposição de passagem da corrente elétrica em um circuito elétrico. Diferenciam-se principalmente por a resistência elétrica ser uma propriedade do corpo e a resistividade elétrica ser uma propriedade do material do qual o corpo foi fabricado. Para saber mais sobre a resistividade elétrica, clique aqui.

Efeito Joule

Também chamado de efeito térmico, o efeito Joule é um fenômeno físico que permite que a energia elétrica seja transformada em energia térmica, calor. Esse efeito acontece tanto em materiais condutores quanto em materiais isolantes, contanto que tenham uma resistência elétrica não nula, ocorrendo então em diversos equipamentos ou aparelhos elétricos, como chuveiros, cafeteiras, celulares, televisores, pipoqueiras, sanduicheiras, liquidificadores, notebooks e diversos outros. Saiba mais sobre o efeito Joule clicando aqui.

Exercícios resolvidos sobre resistência elétrica

Questão 1

(Enem) A resistência elétrica de um fio é determinada pelas suas dimensões e pelas propriedades estruturais do material. A condutividade (σ) caracteriza a estrutura do material, de tal forma que a resistência de um fio pode ser determinada conhecendo-se L (comprimento do fio) e A (a área de seção reta). A tabela relaciona o material à sua respectiva resistividade em temperatura ambiente.

Mantendo-se as mesmas dimensões geométricas, o fio que apresenta menor resistência elétrica é aquele feito de:

A) tungstênio

B) alumínio

C) ferro

D) cobre

E) prata

Resolução:

Alternativa E.

O fio que apresenta menor resistência elétrica é aquele feito de prata, já que ele é o que apresenta a maior condutividade elétrica, grandeza física inversamente proporcional à resistência elétrica.

Questão 2

(UCSal) Um resistor de 100 Ω é percorrido por uma corrente elétrica de 20 mA. A ddp entre os terminais do resistor, em Volts, é igual a:

A) 2,0

B) 5,0

C) 2,0∙10

D) 2,0∙10³

E) 5,0∙ 10³ 

Resolução:

Alternativa A.

Calcularemos a ddp entre os terminais a partir da fórmula da primeira lei de Ohm:

\(U = R \cdot i\)

\(U = 100 \cdot 20m\)

O m de 20mΩ é mili, que significa \({10} ^ {-3}\):

\(U = 100 \cdot 20 \cdot 10^{-3} \)

\(U = 2000 \cdot 10^{-3} \)

\(U = 2 \cdot 10^3 \cdot 10^{-3} \)

\(U = 2\cdot {10} ^ {3-3}\)

\(U = 2 \cdot 10^0 \)

\(U = 2\cdot1\)

\(U = 2 V\)

Fontes

NUSSENZVEIG, Herch Moysés. Curso de física básica: Eletromagnetismo (vol. 3). Editora Blucher, 2015.

SAMPAIO, José Luiz; CALÇADA, Caio Sérgio. Universo da Física: Ondulatória. Eletromagnetismo, Física Moderna. São Paulo: Atual, 2005.