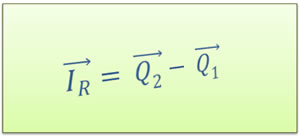A quantidade de movimento (ou momento linear) é uma das grandezas mais importantes na Física, já que está diretamente relacionada à força, ao impulso e à energia cinética. Sua unidade de medida é o quilograma-metro por segundo, pois ela é calculada através do produto entre a massa e a velocidade linear de um corpo.
Leia também: O que é o momento angular?
Tópicos deste artigo
- 1 - Resumo sobre quantidade de movimento
- 2 - O que é quantidade de movimento?
- 3 - Fórmulas da quantidade de movimento
- 4 - Unidade de medida da quantidade de movimento
- 5 - Conservação da quantidade de movimento
- 6 - Relação entre quantidade de movimento e impulso
- 7 - Exercícios resolvidos sobre quantidade de movimento
Resumo sobre quantidade de movimento
-
A quantidade de movimento (ou momento linear) é o produto entre a massa e a velocidade linear de um corpo.
-
A unidade de medida da quantidade de movimento é o quilograma-metro por segundo.
-
A conservação da quantidade de movimento ocorre em sistemas fechados e isolados de quaisquer forças externas.
-
A quantidade de movimento antes da colisão precisa ser igual à quantidade de movimento depois da colisão para ocorrer a conservação da quantidade de movimento.
-
A conservação da quantidade de movimento ocorre sempre em colisões perfeitamente elásticas.
-
O impulso é uma grandeza física vetorial igual à variação do momento linear.
O que é quantidade de movimento?
Comumentemente chamada de momento linear, a quantidade de movimento é uma grandeza física vetorial que pode ser definida como a multiplicação da massa de um corpo pela sua velocidade linear durante um deslocamento. Por ser uma grandeza vetorial ela precisa ser caracterizada em termos da sua orientação e intensidade, em que:
-
Direção: mesma da velocidade.
-
Sentido: mesmo da velocidade.
-
Intensidade: multiplicação da massa com a velocidade.
Fórmulas da quantidade de movimento
A principal fórmula da quantidade de movimento é a seguinte:
\(p=m \cdot v\)
-
p → quantidade de movimento ou momento linear, medida em quilograma-metro por segundo [kg∙m/s].
-
m → massa, medida em quilogramas [kg].
-
v → velocidade, medida em metros por segundo [m/s].
Exemplo:
Determine a quantidade de movimento de uma pessoa de 100 kg que corre a 3 m/s.
Resolução:
\(p=m\cdot v\)
\(p=100\cdot3\)
\(p = 300 \, \text{kg} \cdot \text{m/s} \)
A seguir, outras fórmula ligadas à quantidade de movimento.
→ Força relacionada à quantidade de movimento
\(F = \frac{\Delta p}{\Delta t} \)
-
F → força resultante, medida em Newton [N].
-
\(∆p\) → variação da quantidade de movimento ou momento linear, medida em Newton-segundo [N∙s].
-
\(∆t\) → variação de tempo, medida em segundos [s].
Exemplo:
Determine a quantidade de movimento em uma caixa que está sujeita a uma força de 200 N durante 10 segundos.
Resolução:
\(F = \frac{\Delta p}{\Delta t} \)
\(\Delta p = F \cdot \Delta t \)
\(\Delta p = 200 \cdot 10 \)
\(\Delta p = 2000 \, \text{kg} \cdot \text{m/s} \)
→ Energia cinética relacionada à quantidade de movimento
\(E_{c} = \frac{p^{2}}{2 \cdot m} \)
-
\({E_c}\) → energia cinética, medida em Joule [J].
-
p → quantidade de movimento ou momento linear, medida em [kg∙m/s].
-
m → massa, medida em quilogramas [kg].
Exemplo:
Determine a quantidade de movimento de um automóvel de 900 kg que se movimenta com uma energia cinética de 330 000 J.
Resolução:
\(E_{c} = \frac{p^{2}}{2 \cdot m} \)
\(p^{2} = E_{c} \cdot 2 \cdot m \)
\(p^{2} = 330000 \cdot 2 \cdot 900 \)
\({p} ^ {2} =594 000 000\)
\(p= \sqrt {594 000 000}\)
\(p≅24 372,1 kg\cdot m/s\)
Unidade de medida da quantidade de movimento
De acordo com o Sistema Internacional de Unidades (S.I.), a unidade de medida da quantidade de movimento é o quilograma-metro por segundo, representado por kg∙m/s; também é comum expressar a quantidade de movimento em Newton-segundo, representado por N∙s.
Conservação da quantidade de movimento
A conservação da quantidade de movimento só ocorre quando o sistema está isolado de quaisquer forças externas e fechado, ou seja, não pode haver uma força impedindo o movimento nem pode surgir um corpo que não estava sendo considerado desde o início, respectivamente, caso contrário teremos interferência na quantidade de movimento inicial ou na quantidade de movimento final.
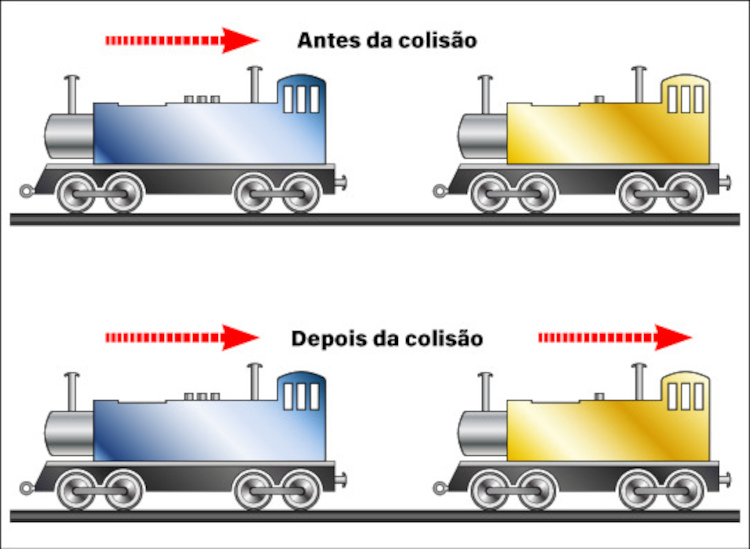
Por exemplo, na colisão perfeitamente elástica entre dois corpos temos a conservação total da quantidade de movimento, o que significa que a quantidade de movimento antes da colisão entre eles é igual à quantidade de movimento depois da colisão entre eles, representado matematicamente pela fórmula:
\(p_{A} + p_{B} = p_{A'} + p_{B'} \)
-
\({p_A}\) e \({p_B}\) → quantidades de movimento do corpo A e B inicial, respectivamente, medidas em quilograma-metro por segundo [kg∙m/s].
-
\({p_A}\) e \({p_B}\) → quantidades de movimento do corpo A e B final, respectivamente, medidas em quilograma-metro por segundo [kg∙m/s].
Para saber mais sobre a conservação da quantidade de movimento, clique aqui.
Relação entre quantidade de movimento e impulso
O impulso é uma grandeza física vetorial medida em quilograma-metro por segundo, assim como a quantidade de movimento, que pode ser definida como a variação da quantidade de movimento de um corpo, o que significa que se empregarmos um impulso a certo corpo, teremos alteração na sua quantidade de movimento.
Como vimos, a quantidade de movimento é calculada principalmente pela seguinte fórmula:
\(p=m \cdot v\)
-
p → quantidade de movimento ou momento linear, medida em quilograma-metro por segundo [kg∙m/s].
-
m → massa, medida em quilogramas [kg].
-
v → velocidade, medida em metros por segundo [m/s].
Já o impulso é calculado através da fórmula:
\(I=∆p\)
-
I → impulso, medido em Newton-segundo [N∙s].
-
∆p → variação da quantidade de movimento ou momento linear, medida em quilograma-metro por segundo [kg∙m/s].
O impulso também pode ser calculado através da seguinte fórmula:
\(I = F \cdot \Delta t \)
-
I → impulso, medido em Newton-segundo [N∙s].
-
F → força resultante, medida em Newton [N].
-
∆t → variação de tempo, medida em segundos [s].
Para saber mais sobre o impulso, clique aqui.
Exercícios resolvidos sobre quantidade de movimento
Questão 1
(Unipac) Um automóvel cuja massa é de 900 kg desenvolve velocidade de 108 Km/h (30 m/s), quando o motorista pisa bruscamente no freio e, com desaceleração constante, consegue parar após 5,0 segundos. Pode-se afirmar que a variação da quantidade de movimento do automóvel foi:
A) \(5,4 \cdot 10^{3} \, \text{N} \cdot \text{s} \)
B) \(2,7 \cdot 10^{4} \, \text{N} \cdot \text{s} \)
C) \(9,7\cdot {10} ^ {4} N\cdot s\)
D) zero
Resolução:
Alternativa B.
Calcularemos a variação da quantidade de movimento do automóvel através fórmula que relaciona o impulso à quantidade de movimento:
\(I=∆p\)
\(F\cdot ∆t=∆p\)
\(m \cdot a \cdot \Delta t = \Delta p \)
\(m \cdot \frac{\Delta v}{\Delta t} \cdot \Delta t = \Delta p \)
\(m \cdot \Delta v = \Delta p \)
\(900 \cdot (0 - 30) = \Delta p \)
\(900 \cdot (-30) = \Delta p \)
\(-27 000=∆p\)
\(-2,7 \cdot 10^{4} = \Delta p \)
Em módulo:
\(2,7 \cdot 10^{4} \, \text{N} \cdot \text{s} = \Delta p \)
Questão 2
(Enem) Durante um reparo na estação espacial internacional, um cosmonauta, de massa 90 kg, substitui uma bomba do sistema de refrigeração, de massa 360 kg, que estava danificada. Inicialmente, o cosmonauta e a bomba estão em repouso em relação à estação. Quando ele empurra a bomba para o espaço, ele é empurrado no sentido oposto. Nesse processo, a bomba adquire uma velocidade de 0,2 m/s em relação à estação.
Qual é o valor da velocidade escalar adquirida pelo cosmonauta, em relação à estação, após o empurrão?
A) 0,05 m/s
B) 0,20 m/s
C) 0,40 m/s
D) 0,50 m/s
E) 0,80 m/s
Resolução:
Alternativa E.
Calcularemos a velocidade adquirida pelo cosmonauta através da conservação da quantidade de movimento, no qual as velocidades apresentam sentidos opostos.
\(p_{1} = p_{2} \)
\(m_{1} \cdot v_{1} = m_{2} \cdot v_{2} \)
\(360 \cdot 0,2 = 90 \cdot v_{2} \)
\(72 = 90 \cdot v_{2} \)
\(v_{2} = \frac{72}{90} \)
\({v_2} =0,8 m/s\)
Fontes
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.