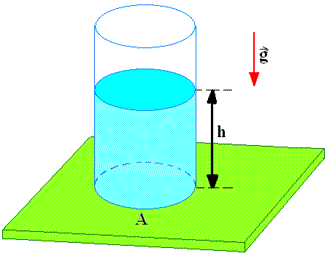
Nos estudos sobre dinâmica, vimos que o conceito de pressão é a grandeza dada pela intensidade da força aplicada sobre uma superfície, por unidade de área. Sendo que a unidade de medida da pressão é o Pa (Pascal), que é igual à força (newton) / área (m2).
Agora nosso objeto de estudo está relacionado à pressão que uma coluna líquida exerce sobre uma superfície. Sendo assim, consideremos a situação da figura acima, em que um tubo, cuja área da base é A, contém um líquido de densidade d, até uma altura h. Vamos calcular a pressão exercida por essa coluna líquida sobre a base do tubo.
O volume do líquido é dado por:
V=Abase . haltura
Sendo d a densidade do líquido, sua massa será dada por:
m=d .V
E seu peso é calculado através da seguinte equação:
P=m . g
Dessa forma, podemos relacionar as equações descritas acima, da seguinte maneira:

Sendo p a pressão exercida no fundo, temos:

A equação acima também é chamada de pressão hidrostática. É importante ficarmos atentos ao fato de essa equação não depender da área da base.