O movimento circular uniformemente variado (MCUV) é definido pela variação da velocidade do corpo enquanto ele executa um trajeto curvilíneo. Essa alteração na velocidade angular ocorre devido à presença de uma aceleração linear, que é tangente ao movimento. Sendo assim, no MCUV existem duas acelerações: a aceleração centrípeta e a aceleração linear. O movimento circular uniformemente variado tem um exemplo bem definido no loop da montanha russa. Na parte da decida, a velocidade é maior do que na parte da subida, já que a decida se dá no mesmo sentido da gravidade, e a subida se dá contra ela.
Leia também: O que é um movimento uniforme?
Tópicos deste artigo
- 1 - Resumo sobre movimento circular
- 2 - O que é movimento circular uniformemente variado (MCUV)?
- 3 - Tipos de aceleração do movimento circular uniformemente variado (MCUV)
- 4 - Fórmulas do movimento circular uniformemente variado (MCUV)
- 5 - Diferenças entre MCUV e MCU
- 6 - Exercícios resolvidos sobre movimento circular uniformemente variado
Resumo sobre movimento circular
-
O movimento circular uniformemente variado (MCUV) é caracterizado pela variação da velocidade no decorrer do trajeto da curva ou círculo descrito pelo movimento.
-
No movimento circular uniformemente variado há duas acelerações: centrípeta e linear.
-
A aceleração centrípeta é direcionada para o centro da curva, realizada durante o movimento, por isso é do tipo radial. É perpendicular à velocidade linear, logo muda sua direção, mas não afeta seu módulo.
-
A aceleração linear é tangencial ao movimento, responsável pela variação da velocidade escalar. Ela afeta o módulo da velocidade linear.
-
A aceleração resultante do movimento equivale à soma vetorial entre a aceleração centrípeta e a aceleração tangencial.
-
A aceleração angular é o fator responsável pela variação da velocidade angular. Trata-se da razão entre a variação da velocidade angular e o tempo necessário para que essa variação ocorra.
-
No movimento circular uniforme (MCU), a velocidade linear é constante; consequentemente, a velocidade angular também, já que são relacionadas.
-
A diferença entre o MCU e MCUV é que no primeiro, a velocidade é constante, pois a aceleração é perpendicular ao deslocamento. Já no segundo, ela sofre variação, devido à presença da aceleração linear.
O que é movimento circular uniformemente variado (MCUV)?
O movimento circular uniformemente variado (MCUV) é um movimento que descreve uma circunferência ou parte dela variando sua velocidade em algumas etapas do deslocamento, devido à presença de uma aceleração linear que faz com que a velocidade linear do deslocamento mude e, consequentemente, a velocidade angular também.
Tipos de aceleração do movimento circular uniformemente variado (MCUV)
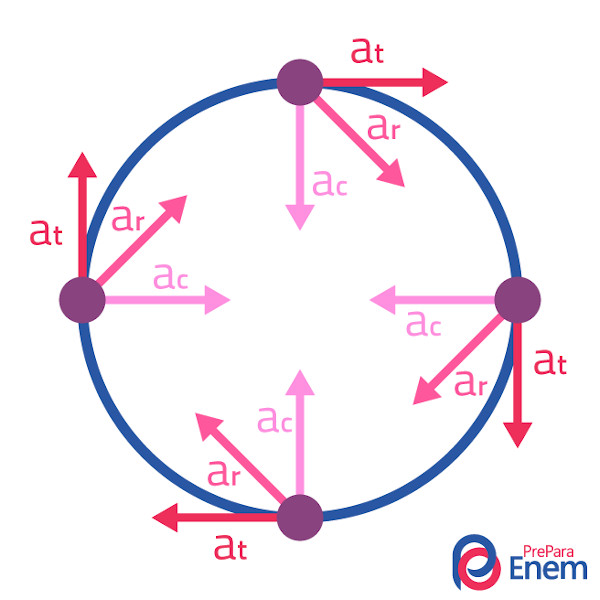
No movimento circular uniformemente variado (MCUV), há quatro tipos de aceleração. Veremos cada uma delas a seguir.
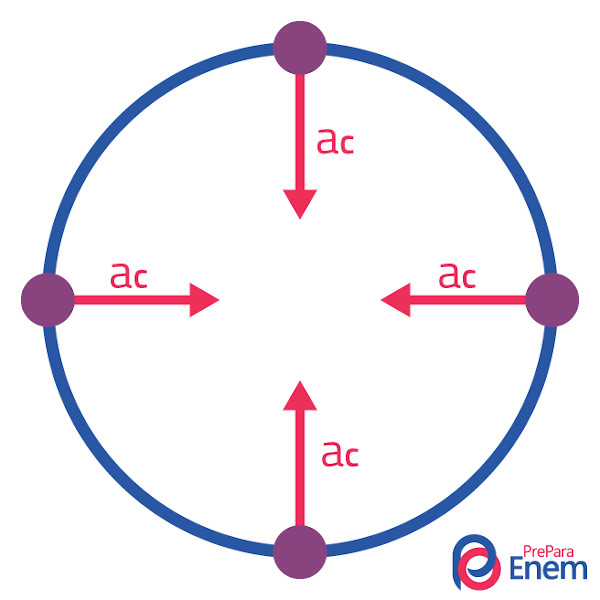
→ Aceleração centrípeta
A aceleração centrípeta é também chamada de radial por possuir a direção do raio da circunferência com sentido para seu centro. Não influencia o valor numérico (módulo) da velocidade linear, já que é perpendicular a ela, porém é o que faz com que o movimento seja circular.
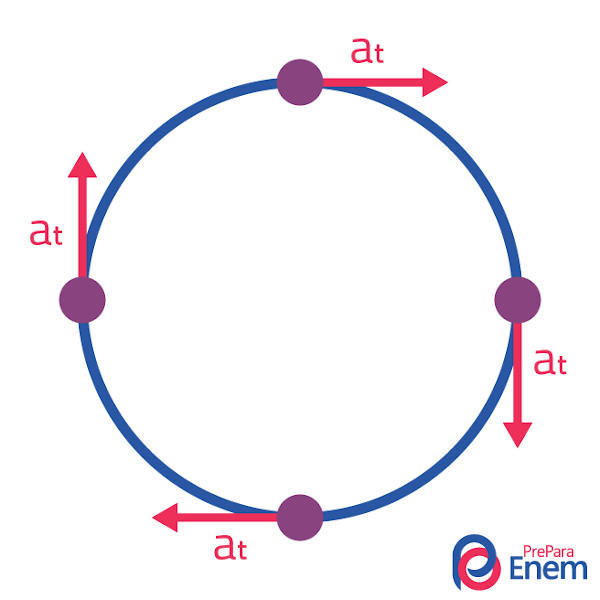
→ Aceleração tangencial
A aceleração tangencial é a aceleração linear, chamada de tangencial nesse tipo de movimento. É tangente ao movimento por possuir uma direção retilínea. É responsável por alterar o módulo da velocidade linear e, consequentemente, da angular. Ou seja, é devido à sua presença que o movimento é considerado circular uniformemente variado.
→ Aceleração resultante
A aceleração resultante é a soma vetorial das acelerações centrípeta e tangencial, que são perpendiculares. É obtida por meio do teorema de Pitágoras, em que os catetos são as acelerações centrípeta e tangencial e a resultante ocupa a posição da hipotenusa.
\(a_R^2=a_c^2+a_t²\)
→ Aceleração angular
A aceleração angular é o fator que faz com que a velocidade angular varie com o tempo. Ela é a razão entre a aceleração tangencial e o raio do círculo descrito no movimento.
Fórmulas do movimento circular uniformemente variado (MCUV)
No MCUV, as fórmulas são similares às do movimento retilíneo uniformemente variado. A diferença é que o deslocamento é a variação do ângulo θ. Veja a seguir:
|
Movimento retilíneo uniformemente variado |
Movimento circular uniformemente variado |
|
\(v=\omega\bullet R\) |
\(\omega=\frac{v}{R}\) |
|
\(a_t=a=\alpha.R\) |
\(\alpha=\frac{a}{R}\) |
|
\(v=v_0+a\bullet t\) |
\(\omega=\omega_0+\alpha\bullet t\) |
|
\(s=s_0+v_0\bullet t+\frac{a∙t^2}2\) |
\(\theta=\theta_0+\omega_0\bullet t+\frac{\alpha\bullet t^2}{2}\) |
|
\(v^2=v_0^2+2\bullet a\bullet∆s\) |
\(\omega^2=\omega_0^2+2\bullet\alpha\bullet∆θ\) |
|
\(a_m=\frac{∆v}{∆t}\) |
\(\alpha_m=∆ω∆t\) |
|
\(a_c=\frac{v^2}{R}\) |
\(a_c=\omega^2\bullet R\) |
|
\(a_R^2=a_c^2+a_t^2\) |
|
Os significados das grandezas a seguir estão no Sistema Internacional de Unidades (SI). Logo, se estiverem com valores diferentes em um problema, deverão ser convertidos.
-
v = velocidade linear final ou de chegada (m/s)
-
v0 = velocidade linear inicial ou de partida (m/s)
-
ω = velocidade angular final ou de chegada (rad/s)
-
ω0 = velocidade angular final ou de chegada (rad/s)
-
at = a = aceleração tangencial ou linear (m/s²)
-
α = aceleração angular (rad/s²)
-
t = tempo (s)
-
θ = posição angular final ou chegada (rad)
-
θ0 = posição angular inicial ou partida (rad)
-
s = posição linear final ou chegada (m)
-
s0 = posição linear inicial ou partida (m)
-
ac = aceleração centrípeta (m/s²)
-
R = raio da circunferência descrita pelo movimento (m)
-
Δθ = deslocamento angular (rad)
-
Δs = deslocamento ou distância linear (m)
Diferenças entre MCUV e MCU
-
Movimento circular uniformemente variado (MCUV): caracterizado por haver aceleração tangencial ao movimento, que faz com a velocidade varie no decorrer do trajeto, devido a uma aceleração constante. Por isso, é uniformemente variado.
-
Movimento circular uniforme (MCU): tem velocidade constante, já que a aceleração centrípeta que caracteriza o movimento é perpendicular à velocidade. Assim, ela influencia o seu sentido, mas não o seu módulo.
Resumidamente, o fator decisivo que as diferencia é a aceleração linear, que faz com que o módulo da velocidade linear v varie e, consequentemente, o módulo da velocidade angular também.
Saiba mais: Quais são os temas de Física que mais caem no Enem?
Exercícios resolvidos sobre movimento circular uniformemente variado
Questão 1
Uma partícula é colocada sob a ação de um campo magnético e elétrico simultaneamente, executando um MCUV que descreve uma circunferência com 1,60 metro de raio. Ela foi lançada dentro da região desses campos com velocidade igual a 24 m/s. Sob a ação de uma aceleração 4 rad/s², ela atinge a velocidade de 100,8 m/s. Qual foi o deslocamento angular dessa partícula?
Resolução:
Extraindo os dados do problema:
R = 1,6 m
v = 100,8 m/s
v0 = 24 m/s
α = 4 rad/s²
Δθ = ?
Queremos encontrar o deslocamento angular, então as velocidades lineares devem ser convertidas em velocidades angulares.
\(\omega_0=\frac{v_0}{R}=\frac{24}{1,6}=15\ rad/s\)
\(\omega=\frac{v}{R}=\frac{100,8}{1,6}=63\ rad/s\)
Já que o tempo não foi mencionado no problema, podemos utilizar a equação de Torricelli para o MCUV.
\(\omega^2=\omega_0^2+2\bullet\alpha\bullet∆θ\)
\({63}^2={15}^2+2\bullet4\bullet∆θ\)
\(3969=225+8\bullet∆θ\)
\(3969-225=8\bullet∆θ\)
\(3744=8\bullet∆θ\)
Como a incógnita se encontra após a igualdade, os lados da equação serão invertidos.
\(8\bullet∆θ=3744\)
\(∆θ=\frac{3744}{8}=468\ rad\)
Questão 2
Um barbante de 80 centímetros teve uma de suas extremidades amarrada em uma pequena esfera e a outra, em um suporte. A esfera foi lançada com velocidade de 10 rad/s e parou após 2,5 s, descrevendo parte de uma circunferência. Determine a aceleração linear da esfera.
Resolução:
Extraindo os dados:
R = 80 cm
ω0 = 10 rad/s
ω = 0
t = 2,5 s
a = ?
Como a velocidade angular variou de 10 rad/s para 0, trata-se de movimento circular uniformemente variado.
\(\omega=\omega_0+\alpha\bullet t\)
\(0=10+\alpha\bullet2,5\)
O produto α · 2,5 está depois da igualdade, então ele se deslocará com o sinal invertido.
\(-2,5\bullet\alpha=10\)
\(\alpha=\frac{10}{-2,5}=-4\ rad/s^2\)
O resultado é negativo porque a velocidade diminui. Consequentemente, a esfera desacelera. O valor do raio está em centímetros e deve ser convertido em metros (dividido por 100) para obtermos a aceleração linear.
\(R=\frac{80\ cm}{100}=0,8\ m\)
\(a=\alpha\bullet R=-4\bullet0,8=-3,2\ m/s^2\)