Movimento uniforme é o tipo de movimento que ocorre em trajetória retilínea e com velocidade constante, ou seja, sem que haja aceleração. Quando um móvel encontra-se em movimento uniforme, ele percorre espaços iguais em intervalos de tempo iguais.
Nesse tipo de movimento, a velocidade média de um móvel é igual à sua velocidade instantânea em toda a duração do movimento.
Veja também: Conceitos básicos de Cinemática
Tópicos deste artigo
- 1 - Velocidade média
- 2 - Gráficos do movimento uniforme
- 3 - → Gráfico do movimento uniforme regressivo
- 4 - Exemplos de movimento uniforme
- 5 - Exercício resolvido de movimento uniforme
Velocidade média
O movimento uniforme é caracterizado por uma velocidade constante. Sua velocidade pode ser calculada com base na fórmula seguinte:
![]()
v — velocidade média
ΔS — deslocamento
Δt — intervalo de tempo
De acordo com a fórmula demonstrada, a velocidade média no movimento uniforme é definida pela razão do deslocamento pelo intervalo de tempo. O deslocamento, por sua vez, é calculado pela variação do espaço. O deslocamento é dado pela diferença entre as posições final e inicial de um móvel:
![]()
SF — posição final
S0 — posição inicial
O intervalo de tempo é definido com base nos instantes inicial e final de um movimento:
![]()
tF — instante de tempo final
t0 — instante de tempo inicial
A fórmula de velocidade média, que acabamos de apresentar, pode ser escrita de outra forma, conhecida como função horária da posição. A função horária da posição é uma função de primeiro grau que relaciona a posição do móvel em relação ao tempo:
![]()
S — posição final
S0 — posição inicial
v — velocidade média
t — instante de tempo
Veja também: Velocidade escalar média
Gráficos do movimento uniforme
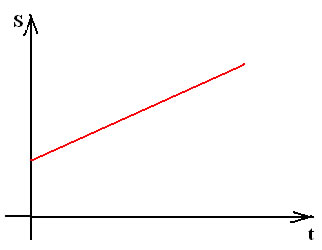
O movimento uniforme pode ser descrito por meio de gráficos de posição e velocidade em função do tempo. No movimento uniforme e progressivo, a posição pode ser definida por um gráfico em formato de uma reta ascendente:
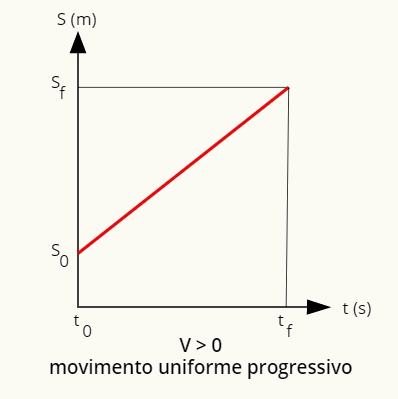
O gráfico da posição no movimento uniforme e progressivo é uma reta ascendente.
No movimento uniforme e regressivo, o gráfico da posição em função do tempo é definido como uma reta descendente:
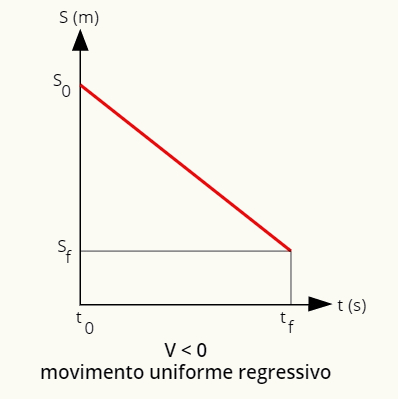
O gráfico da posição para o movimento uniforme e regressivo é uma reta descendente.
O gráfico da posição em função do tempo para quando o móvel encontrar-se em repouso é uma reta paralela ao eixo horizontal:
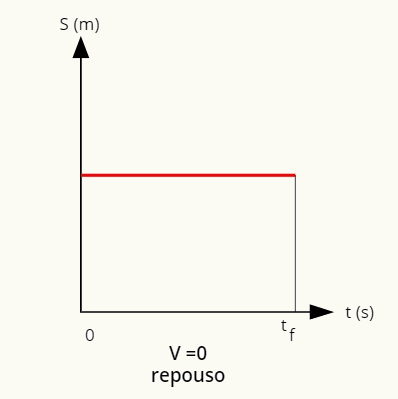
No repouso, a posição é dada por uma reta paralela ao eixo horizontal.
Veja também: Conheça as principais equações da Cinemática
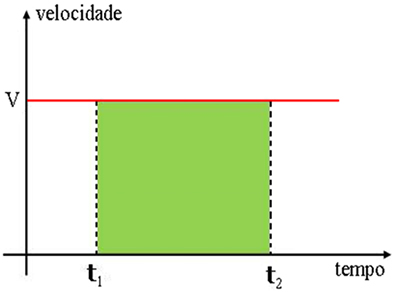
Os gráficos de velocidade para o movimento uniforme são mostrados a seguir:
→ Gráfico do movimento uniforme progressivo
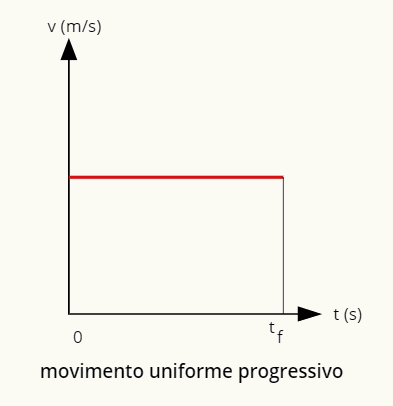
O gráfico do movimento uniforme progressivo é uma reta positiva paralela à horizontal.
→ Gráfico do movimento uniforme regressivo
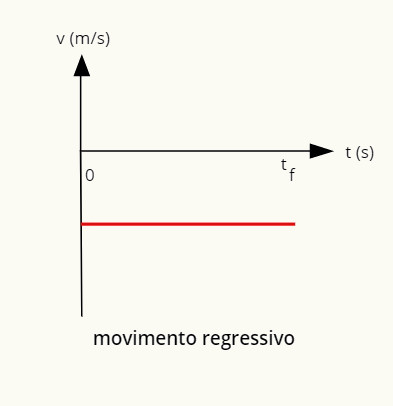
O gráfico do movimento regressivo é uma reta negativa paralela à horizontal.
→ Gráfico de repouso
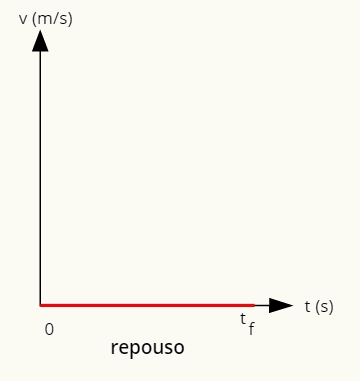
O gráfico que representa o repouso é dado por uma reta sobre o eixo horizontal.
Unidades de velocidade
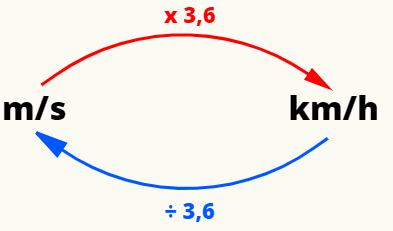
Para convertermos as unidades mais comuns de velocidade — o metro por segundo (m/s) e o quilômetros por hora (km/h) —, podemos fazer a seguinte operação:
Exemplos de movimento uniforme
1) Um trem desloca-se em uma velocidade constante de 20 metros por segundo. Determine o tempo necessário para esse trem percorrer uma distância de 60 metros.
Resolução:
Para resolver esse exercício, utilizaremos a fórmula da velocidade média:
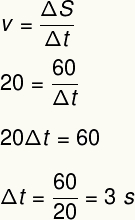
2) Um maratonista percorre uma distância de 4500 m com velocidade média de 3,6 km/h. Determine o tempo necessário para a conclusão dessa prova, em segundos e em horas e minutos.
Resolução:
Para resolver esse exercício, primeiramente é necessário transformar a unidade da velocidade, que está em quilômetros por hora, em metros por segundo:

Exercício resolvido de movimento uniforme
1) (Fuvest) João está parado em um posto de gasolina quando vê o carro de seu amigo passando por um ponto P, na estrada, a 60 km/h. Pretendendo alcançá-lo, João parte com seu carro e passa pelo mesmo ponto P, depois de 4 minutos, já a 80 km/h. Considere que ambos dirigem com velocidades constantes. Medindo o tempo, a partir de sua passagem pelo ponto P, João deverá alcançar seu amigo, aproximadamente, em:
a) 4 minutos
b) 10 minutos
c) 12 minutos
d) 15 minutos
e) 20 minutos
Resolução:
Para resolver esse exercício, precisamos primeiramente determinar o espaço percorrido do amigo de João, considerando que João passa pelo ponto P quatro minutos após a sua passagem. Para tanto, transformamos a velocidade do carro do amigo de João em km/min, dividindo-a por 60, uma vez que cada hora tem 60 minutos.
Em seguida, devemos escrever as funções horárias da posição de cada veículo, com o carro do amigo de João em uma posição inicial de 4 km à sua frente. Em seguida, para que os veículos encontrem-se, suas posições finais precisam ser iguais. Confira a resolução passo a passo: