O movimento circular uniforme (MCU) é aquele em que a velocidade de um corpo se mantém constante enquanto esse corpo executa um trajeto curvilíneo na presença de uma aceleração. A aceleração é a responsável pelo trajeto formar um círculo, já que ela é perpendicular à velocidade, como se fosse direcionada ao centro de uma circunferência, na mesma direção do raio dela. Por causa disso, essa aceleração é chamada de radial ou centrípeta.
Como o trajeto é circular, o deslocamento ocorre como se estivesse abrindo, cada vez mais, um ângulo, logo, ele é chamado de angular, e, como é gasto determinado tempo para ir formando um ângulo cada vez maior, surge a velocidade angular. Como o círculo pode ser contornado várias vezes, surge a frequência do movimento, e o tempo gasto para uma revolução completa do círculo é chamado de período.
Leia também: Conceitos básicos de movimento
Tópicos deste artigo
- 1 - Resumo sobre o movimento circular uniforme (MCU)
- 2 - Características do movimento circular uniforme (MCU)
- 3 - Aceleração centrípeta
- 4 - Grandezas angulares
- 5 - Período e frequência
- 6 - Fórmulas do movimento circular uniforme (MCU)
- 7 - Como se aplica o movimento circular uniforme (MCU)?
- 8 - Exercícios resolvidos sobre o movimento circular uniforme (MCU)
Resumo sobre o movimento circular uniforme (MCU)
- O MCU é caracterizado pela velocidade não sofrer variações no decorrer do trajeto da curva ou círculo descrito pelo movimento.
- A aceleração centrípeta é direcionada para o centro da curva realizada durante o movimento, por isso é do tipo radial.
- A aceleração centrípeta é perpendicular à velocidade linear, logo, muda sua direção, mas não afeta seu módulo.
- A velocidade angular está totalmente relacionada com a velocidade linear, logo, afetando-se uma, a outra também será influenciada.
- A frequência é o número de revoluções completas no círculo no tempo de 1 segundo.
- Período é o tempo gasto para uma revolução completa.
Características do movimento circular uniforme (MCU)
O movimento circular uniforme ocorre quando um corpo, com uma velocidade v constante, está sob ação de uma aceleração perpendicular à sua velocidade, fazendo com que o movimento descrito seja um círculo. Como a aceleração se mantém perpendicular à velocidade, ela se volta para o centro da circunferência.
Aceleração centrípeta
A aceleração voltada para o centro da circunferência descrita pelo movimento é chamada de centrípeta, e como ela está sempre na mesma direção do raio da circunferência, também recebe o nome de radial. Ela é a responsável pelo movimento ser circular. Sendo perpendicular à velocidade, ela altera a direção do corpo, não o módulo da velocidade, nesse caso, esta permanece constante.
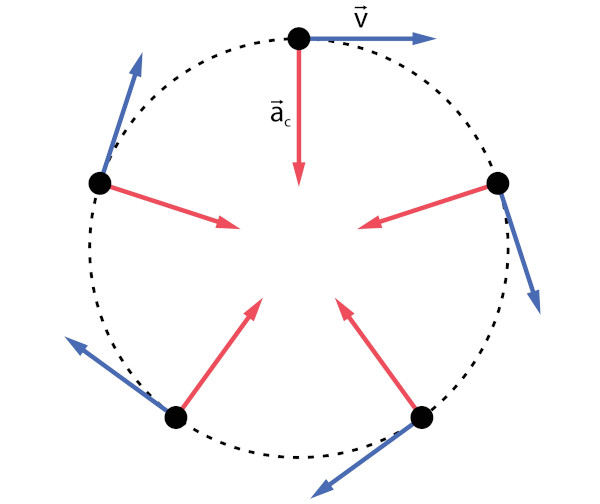
A figura anterior representa o esquema vetorial entre a velocidade linear do corpo, a qual descreve o círculo, e a aceleração centrípeta, que obriga o corpo a realizá-lo.
Grandezas angulares
As grandezas angulares dizem respeito a um movimento que gradualmente forma um círculo, parte dele ou vários ciclos dele. As grandezas angulares estão associadas às grandezas lineares, sendo sempre a razão entre as grandezas lineares e o raio da circunferência descrita.
- Espaço ou posição angular (θ): é o equivalente à posição ou ao espaço linear, ou seja, é o ângulo formado na posição em que o corpo se encontra na circunferência, representado por θ. As unidades de medida são o radiano (rad) ou graus, e a relação entre elas está disposta a seguir.
\(3,14\ rad=180°→π rad=180°\)
Com isso, nota-se que o π rad equivale ao ângulo formado por um hemisfério (metade) de círculo.
- Deslocamento angular (Δθ): é a diferença entre os valores dos ângulos onde o movimento se iniciou e onde o corpo entrou em repouso. Lembrando que uma volta completa equivale a um ângulo de 360º ou 2π rad (radianos) e distância linear percorrida equivale ao comprimento da circunferência (2.π.R). A imagem a seguir representa as posições angulares θ, o deslocamento angular Δθ e a associação com o deslocamento linear Δs.
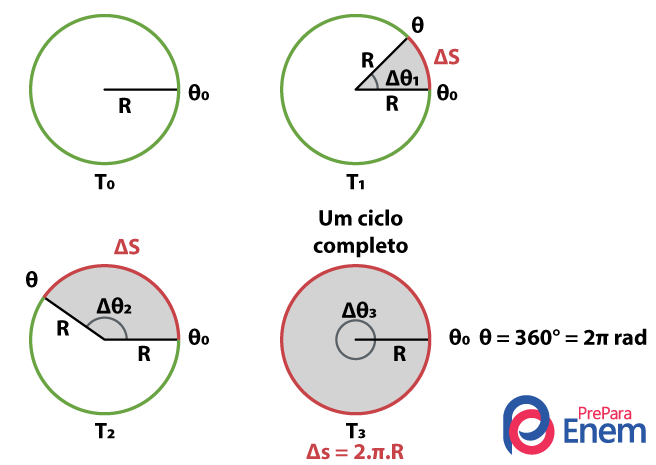
- Velocidade angular (ω): é o deslocamento angular realizado por um corpo em determinado tempo. Trata-se de um conceito bem similar ao da velocidade linear, que, por sua vez, é o deslocamento de um corpo em determinado tempo. A diferença é que, na angular, o deslocamento implica a abertura ou redução de um ângulo. Como a velocidade linear é constante, a velocidade angular também será, e sua unidade de medida é o radiano por segundo (rad/s).
Saiba mais: Relação entre velocidade linear e velocidade angular
Período e frequência
O período (T) é o tempo gasto para um corpo descrever um ciclo inteiro, ou seja, dar uma volta completa em uma circunferência, e é medido em segundos. A frequência (f) é a quantidade de ciclos formados em 1 segundo, e sua unidade de medida é o hertz (Hz). O período é o inverso da frequência, como demonstrado na relação a seguir.
\(T=\frac{1}{f}\ \ \ \ ou\ \ \ \ f=\frac{1}{T}\)
Outra unidade de medida da frequência é a rotação por minuto (rpm), cuja relação com a medida hertz está disposta a seguir.
\(f_{Hz}=\frac{f_{rpm}}{60}\)
Fórmulas do movimento circular uniforme (MCU)
A fórmulas do movimento circular uniforme são similares às do movimento retilíneo uniforme. A diferença é que as posições são substituídas pelos ângulos θ e a velocidade linear v pela velocidade ω. As relações entre elas estão representadas na tabela a seguir.
|
Linear |
Angular |
Relação |
|
s |
θ |
\(s=\theta\cdot\ R\ \ \ \rightarrow\ \ \theta=\frac{s}{R}\) |
|
Δs |
Δθ |
\(∆s=∆θ\cdot R → ∆θ=\frac{∆s}{R} \) |
|
v |
ω |
\(v=\omega\cdot R\ \ \ \rightarrow\ \ \ \omega=\frac{v}{R}\) |
Assim, as equações para movimento circular uniforme, posição angular, velocidade angular e frequência serão descritas a seguir:
|
Posição angular |
\(s=s_0+v.t\ \ \rightarrow\ \ \theta=\theta_0+\omega.t\ \) |
|
Velocidade angular |
\(v=∆s∆t → ω=∆θ∆t\) |
|
Aceleração centrípeta |
\(a_c=\frac{v^2}{R}oua_c=\omega^2\cdot R\) |
|
Associação entre velocidade angular e frequência |
\(\omega=2\cdot\pi\cdot f\ \) Obs.: para essa fórmula, a frequência deve estar medida em hertz e não em rotação por minuto. |
|
Associação entre velocidade angular e período |
\(\omega=\frac{2\cdot\pi}{T}\\\) |
Vale dizer ainda que, para uma volta completa, o deslocamento linear s equivale ao comprimento do círculo:
\(s=2\cdot\pi\cdot R\)
-
Exemplos de aplicações das fórmulas do MCU
1. Uma engrenagem de raio igual a 30 cm gasta 4 segundos para formar 1 radiano. Sabendo que sua velocidade é constante, quais são a velocidade linear e a frequência de giro dessa engrenagem?
Resposta:
Extraindo os dados do problema:
- R = 30 cm
- t = 4 s
- Δθ = 1 rad
- v = ?
- f = ?
Primeiramente o raio que está em centímetros deve ser convertido para metros dividindo-o por 100.
\(R=\frac{30\ cm}{100}=0,3\ m\)
Em seguida, calcula-se a velocidade angular instantânea com o deslocamento angular e o tempo.
\(\omega=\frac{\mathrm{\Delta\theta}}{t}=\frac{1}{4}=0,25\ rad/s\ \)
Calculando a velocidade linear primeiro:
\(v=\omega\cdot R=0,25\cdot0,3=0,075\ m/s\)
Calculando a frequência em seguida:
\(\omega=2\cdot\pi\cdot f\ \ \ \ \)
\(0,25=2\cdot3,14\cdot f\ \ \ \ \)
\(0,25=6,28\cdot f\)
Invertendo os dois lados da equação para a incógnita ficar na posição correta:
\(6,28\cdot f=0,25\)
\(f=\frac{0,25}{6,28}=0,039\approx0,04\ Hz\)
2. Uma centrífuga de um laboratório de análises clínicas tem suas amostras formando um raio de 20 cm. Sabendo que a velocidade linear da centrífuga é 6 m/s, qual a sua aceleração centrípeta?
Resposta:
Extraindo os dados do problema:
- R = 20 cm
- v = 6 m/s
- ac = ?
Primeiramente o raio que está em centímetros deve ser convertido para metros dividindo-o por 100.
\(R=\frac{20\ cm}{100}=0,2\ m\)
Calculando a aceleração centrípeta:
\(a_c=v²R=6²0,2=360,2=180 m/s²\)
Como se aplica o movimento circular uniforme (MCU)?
O movimento circular uniforme é capaz de descrever todo o movimento circular de aceleração nula, ou seja, quando a velocidade é constante, como as órbitas dos planetas em torno do Sol ou dos satélites em torno dos planetas.
Outra aplicação é na associação de engrenagens de uma máquina, como as do relógio. Os relógios mais caros têm suas engrenagens feitas à mão, apresentando uma acurácia de tempo mais precisa do que a medida em relógios digitais comuns.
Outros exemplos são os antigos aparelhos de leitura de mídia física, como discos de vinil, fitas cassete, CD etc. Todos eles reproduziam suas respectivas mídias com velocidade constante, e, para isso, era necessário rotacionar a mídia ou parte dela de alguma forma.
Leia também: Física do Hand Spinner — brinquedo com funcionamento ligado ao movimento circular
Exercícios resolvidos sobre o movimento circular uniforme (MCU)
Questão 1
Maria possui uma vitrola (dispositivo que reproduz músicas por meio de discos de vinil), e, por curiosidade, fez uma marcação com giz na extremidade de um de seus discos e cronometrou o tempo gasto para a agulha passar novamente pela marcação. O tempo registrado foi 10 segundos, sendo assim, a frequência de rotação e a velocidade angular do disco na vitrola serão de:
a) 0,1 Hz e 0,628 rad/s
b) 10 Hz e 554 rad/s
c) 5 Hz e 12 rad/s
d) 2 Hz e 8 rad/s
e) 62 Hz e 4 rad/s
Resposta: letra A
Extraindo os dados:
- T = 10 s (É o conceito de período.)
- f = ?
- ω = ?
Calculando primeiro a frequência:
\(f=\frac{1}{T}=\frac{1}{10}=0,1\ Hz\)
Em seguida, calcula-se a velocidade angular:
\(\omega=2\cdot\pi\cdot f=2\cdot3,14\cdot0,1=0,628\ rad/s\)
Questão 2
Determinado carro descreveu uma curva de raio de 8 metros. Com sua velocidade constante, sua aceleração centrípeta foi de 128 m/s². Sabendo disso, pode-se afirmar que a velocidade angular desse carro é:
a) 12 rad/s
b) 20 rad/s
c) 16 rad/s
d) 15 rad/s
e) 4 rad/s
Resposta: letra E
Extraindo os dados do problema:
- ac = 128 m/s²
- R = 8 m
- ω = ?
\(a_c=\omega^2\cdot R\ \ \)
\(128=\omega^2\cdot8\ \ \)
Invertendo os dois lados da equação, para a incógnita ficar na posição correta:
\(\omega^2\cdot8=128\)
\(\omega^2=\frac{128}{8}\ \ \)
\(\omega^2=16\)
Como a incógnita está elevada ao quadrado, acrescenta-se um radical aos dois lados da equação, assim ele se anulará com o expoente.
\(\sqrt{\omega^2}=\sqrt{16}\)
\(\omega=4\ rad/s\)