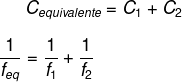Lentes esféricas

As lentes esféricas são um sistema óptico formado por materiais como vidro e acrílico, que refratam a luz visível. São formadas por meios homogêneos e transparentes e podem ser classificadas como côncavas ou convergentes, ou seja, de bordas grossas ou bordas finas.

A partir de elementos da lente, como sua geometria e seu índice de refração (dificuldade de passagem da luz), é possível determinar o tamanho e posição da imagem formada, que pode ser real ou virtual. Essa capacidade de defletir os raios de luz, isto é, o que conhecemos como o grau da lente, é chamada de vergência ou dioptria.

Leia também: Óptica no Enem — como esse assunto é cobrado?

Tópicos deste artigo

• 1 - Resumo sobre lentes esféricas
• 2 - Propriedades das lentes esféricas
• 3 - Usos das lentes esféricas
• 4 - Tipos de lentes esféricas
• 5 - Elementos geométricos das lentes esféricas
• 6 - O que são raios notáveis nas lentes esféricas?
• 7 - Formação de imagens nas lentes esféricas
• 8 - Fórmulas das lentes esféricas
• 9 - Vergência das lentes esféricas
• 10 - Justaposição das lentes esféricas
• 11 - Videoaula sobre óptica no Enem

Resumo sobre lentes esféricas

• As lentes esféricas são sistemas ópticos formados por meios homogêneos e transparentes.

• As lentes esféricas são capazes de refratar a luz e formar imagens virtuais ou reais.

• Há duas classificações para as lentes esféricas: côncavas ou convexas.

• O sistema óptico de lentes esféricas possui cinco pontos geométricos: centro óptico, pontos antiprincipais da imagem e do objeto e focos da imagem e do objeto.

• A distância do ponto antiprincipal até o centro óptico possui o mesmo valor do raio de curvatura da lente esférica.

• A distância entre o foco e o centro óptico, a distância focal, é a metade do valor do raio de curvatura.

• É possível encontrar as imagens formadas pela lente esférica através dos métodos analítico ou gráfico.

• O grau da lente esférica, ou a capacidade de defletir a luz, é chamado de vergência ou dioptria (di).

• As lentes esféricas são utilizadas em diversos equipamentos, como óculos, telescópios, microscópios, celulares, projetores, câmeras, lupas, entre outros.

• Para formação de imagem no método gráfico, basta utilizar os quatro raios notáveis.

• Quando combinamos duas ou mais lentes, ocorre a justaposição de lentes esféricas e basta somar suas vergências.

Propriedades das lentes esféricas

As propriedades das lentes podem variar dependendo do meio em que estão inseridas. Em meios no qual o índice de refração é menor que o da lente, como o ar, para lentes de vidro e acrílico, as lentes podem convergir ou divergir a luz.

As lentes convexas convergem a luz, ou seja, são capazes de redirecionar todos os raios de luz para um único ponto. Já as lentes côncavas divergem a luz, ou seja, são capazes de redirecionar os raios de luz para diferentes pontos.

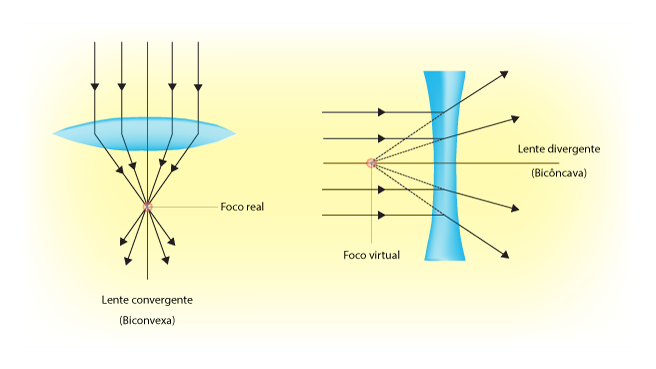
Por isso, podemos subdividir a classificação das lentes em convergente ou divergente.

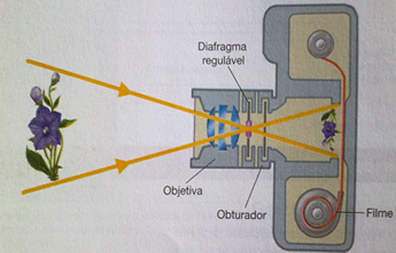
Usos das lentes esféricas

As lentes esféricas são utilizadas em diversos dispositivos de observação, como lunetas, telescópios, microscópios e lupas, além de dispositivos como câmeras, celulares e projetores. Também se destaca seu uso no cotidiano no que se refere à correção de problemas de visão — em óculos, as lentes são capazes de corrigir condições como miopia, hipermetropia, astigmatismo, entres outras.

Leia também: Conceitos que causam dúvidas em Óptica

Tipos de lentes esféricas

Há duas classificações de lentes esféricas: lentes côncavas e lentes convexas. Porém, ainda é possível subdividir essas classificações.

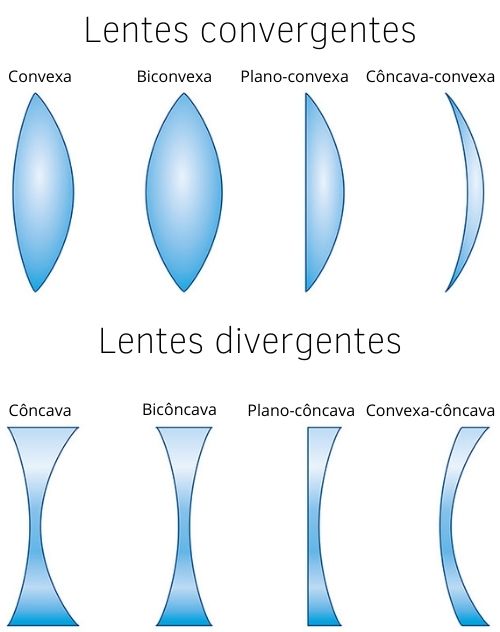
Dentre as convexas, podemos encontrar três tipos de formatos:

• Biconvexa: quando as duas bordas são convexas.

• Plano-Convexa: quando uma borda é plana e a outra é convexa.

• Côncava-Convexa: quando uma borda é côncava e a outra borda, convexa.

Dentre as côncavas, também podemos encontrar três tipos de formatos:

• Bicôncava: quando as duas bordas são côncavas.

• Plano-Côncava: quando uma borda é plana e a outra é côncava.

• Convexa-Côncava: quando uma borda é convexa e a outra, côncava.

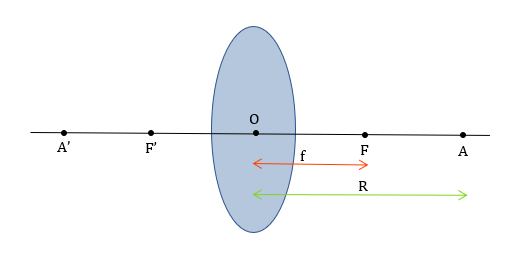
Elementos geométricos das lentes esféricas

No estudo das lentes esféricas, é definido um sistema óptico, independentemente de a lente ser côncava ou convexa, para identificar seus elementos geométricos, sendo eles:

• Centro óptico (O);

• Foco principal do objeto (F);

• Foco principal da imagem (F’);

• Ponto antiprincipal do objeto (A);

• Ponto antiprincipal da imagem (A’).

O centro óptico (O) da lente fica exatamente em seu centro geométrico. A distância do centro até o foco é chamado de distância focal (f) e essa distância tem o mesmo valor da metade do raio da lente (R/2). Já a distância do centro óptico até o ponto antiprincipal (A) é conhecido como raio de curvatura (R).

A linha que traça esses pontos é o eixo de simetria para definir o referencial de Gauss, que indica se os valores encontrados para cada ponto será positivo ou negativo. Para essa convenção de sinais, determina-se que:

• qualquer ponto que esteja acima e/ou à direita do eixo de simetria possui sinal positivo;

• qualquer ponto que esteja abaixo e/ou à esquerda do eixo de simetria possui sinal negativo.

O que são raios notáveis nas lentes esféricas?

Os raios notáveis são representações de feixes de luz que passam pela lente, nos pontos geométricos, na formação de imagens.

Para encontrar a imagem, utilizando o método gráfico (utilizando os raios notáveis para encontrar a imagem no sistema óptico), aplicam-se os quatro raios notáveis:

• o que incide paralelamente e refrata para o foco da imagem;

• o que incide pelo centro óptico;

• o que incide pelo foco do objeto e refrata paralelamente;

• o que passa pelo ponto antiprincipal.

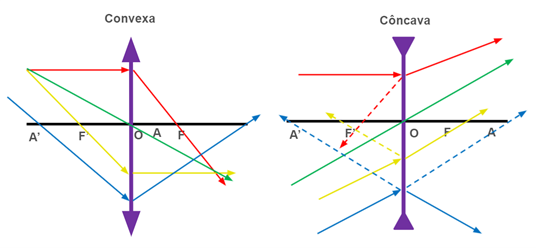
Para as lentes côncavas, o prolongamento dos raios é que formará a imagem.

Formação de imagens nas lentes esféricas

Na formação de imagem, no método gráfico, é necessário utilizar pelo menos dois dos quatro raios notáveis. O encontro desses dois raios é o ponto da formação da imagem, que pode ser virtual ou real.

• Imagem virtual: é formada no mesmo lado que o objeto, pelo prolongamento dos raios de luz. Essa imagem é direita e não pode ser projetada.

• Imagem real: é formada no lado oposto do objeto, pelo cruzamento dos raios de luz. Essa imagem é invertida e pode ser projetada.

A formação da imagem também depende da posição do objeto e do tipo de lente. Para o caso de uma lente convexa, de bordas finas, há cinco formas de posicionar o objeto:

1. Antes do ponto antiprincipal:

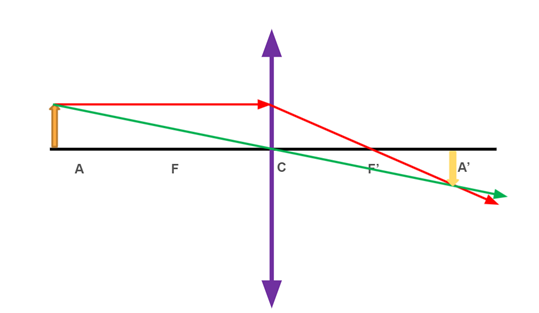
Nessa situação, a imagem formada é real, invertida e menor que o objeto.

2. No ponto antiprincipal:

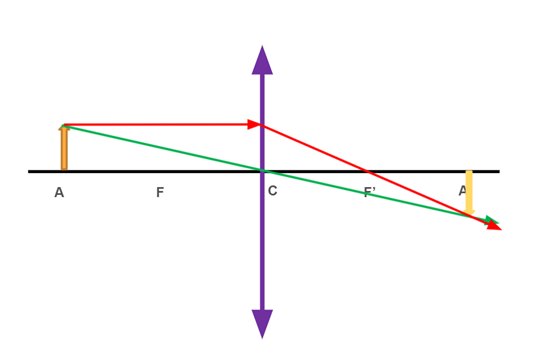
Nessa situação, a imagem formada é real, invertida e do mesmo tamanho do objeto. Aqui, o único raio não passível de utilização é o que passa pelo ponto antiprincipal.

3. Entre o foco e o ponto antiprincipal:

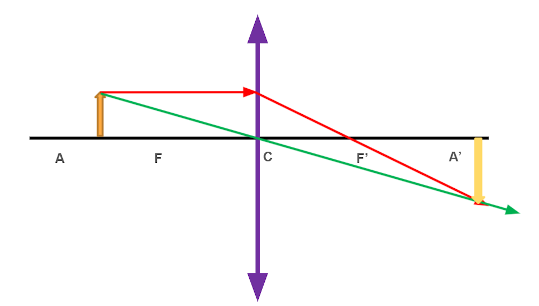
Nessa situação, a imagem formada é real, invertida e maior que o objeto.

4. No foco:

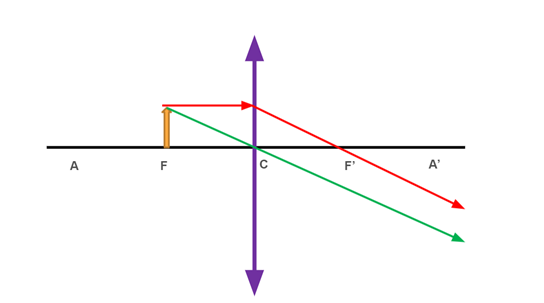
Nessa situação, os raios não se cruzam, portanto, não há formação de imagem. Podemos dizer também que a imagem é imprópria. Aqui, o único raio não passível de utilização é o que incide pelo foco e refrata paralelamente.

5. Entre o foco e o centro óptico:

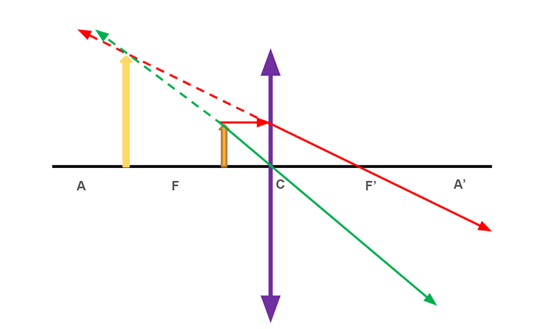
Nessa situação, os raios não se cruzam. O prolongamento deles é que forma a imagem, que é virtual, direita e maior que o objeto.

Para as lentes côncavas, de bordas grossas, existe apenas uma possibilidade de formação de imagem, independentemente da posição do objeto.

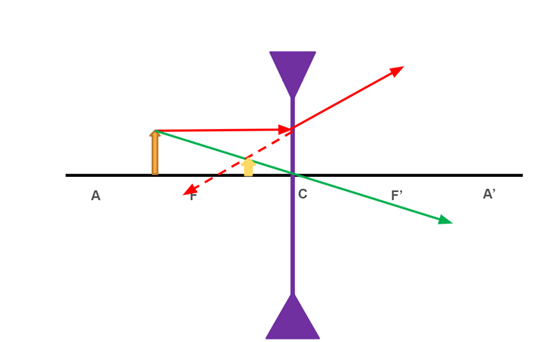
Toda imagem formada por uma lente côncava será virtual, direita e menor que o objeto.

Fórmulas das lentes esféricas

Para encontrar o aumento linear da imagem em relação ao objeto, podemos utilizar:

• A: aumento linear;

• i: tamanho da imagem;

• o: tamanho do objeto;

• p’: posição da imagem;

• p: posição do objeto;

• f: distância focal.

Para encontrar a distância focal ou vergência, deve-se utilizar a equação de Gauss:

• Quando a distância focal é um valor positivo (f > 0), sabemos que se trata de uma lente convergente;

• Quando a distância focal é um valor negativo (f > 0), sabemos que se trata de uma lente divergente.

Para encontrar a vergência através das informações do meio onde a lente está imersa, podemos utilizar a equação do fabricante de lentes, conhecida como equação de Halley:

• n: índice de refração;

• R: raio de curvatura.

Leia também: Espelhos esféricos e equação de Gauss

Vergência das lentes esféricas

A vergência ou convergência representa o quanto a lente é capaz de desviar a luz que chega até ela. É o que conhecemos como grau da lente.

Ela é simbolizada pela letra C, possui o mesmo valor que o inverso da distância focal e pode ser encontrada da seguinte maneira:

Quando a vergência apresenta um valor positivo, significa que se trata de uma lente convergente, enquanto um valor negativo indica uma lente divergente.

Dioptria das lentes esféricas

A dioptria é a unidade de medida da vergência, que é representada por di ou m^-1.

Justaposição das lentes esféricas

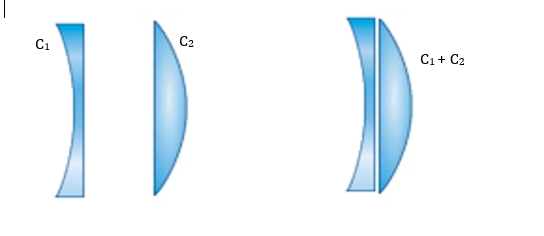
Para a obtenção de diferentes configurações na formação de imagens, é possível combinar duas ou mais lentes de forma justaposta.

Essa combinação pode potencializar o efeito da lente, como em telescópios e microscópios, ou até reduzir o efeito conhecido como aberração cromática, que ocorre quando a luz branca passa pela lente e, devido à sua curvatura, essa luz é decomposta como em um prisma.

Para calcular a vergência da justaposição, basta somar a vergência das lentes combinadas:

Videoaula sobre óptica no Enem