Não é de hoje que conhecemos os espelhos. Diz a história dos espelhos que eles foram primeiramente fabricados pelos egípcios. Eles conseguiam obter espelhos das superfícies polidas de metais como o bronze, a prata, o cobre, etc. Vejamos algumas características dos espelhos planos.
Ponto objeto: é o ponto de convergência dos raios de luz que incidem no sistema óptico S (espelhos, dioptros, lentes, etc.). Fisicamente podemos determinar o ponto objeto através do prolongamento dos raios de luz.
Ponto imagem: é o ponto de convergência do sistema óptico. Da mesma maneira que o ponto objeto, o ponto imagem pode existir fisicamente pelo prolongamento dos raios de luz.
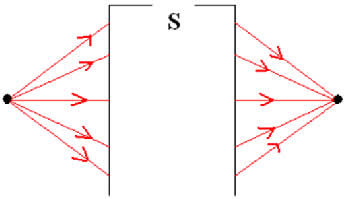
Em física chamamos de Sistema Óptico Estigmático aquele que conjuga um ponto objeto com um ponto imagem, ou seja, há a formação de apenas uma imagem para tal ponto analisado. Ao falarmos de ponto objeto ou ponto imagem estamos considerando um objeto cujas dimensões são tão pequenas que as desprezamos. A figura acima nos mostra o exemplo de um sistema óptico estigmático.
Sendo assim, se o sistema óptico conjugar um ponto objeto que não possa ser considerado como sendo um ponto, ou seja, suas dimensões não podem ser desprezadas, esse sistema óptico não é considerado estigmático. Vejamos a ilustração abaixo.

Representação esquemática de um sistema óptico (S) não estigmático.
Na prática, os sistemas ópticos não estigmáticos têm duas consequências:
1º - não fornecem imagens nítidas
2º - quando o fazem, essa imagem é vista de posições diferentes por observadores diferentes.
Essas consequências, particularmente a primeira, tornam o sistema óptico de pouca utilidade. Além disso, a impossibilidade de definir de forma unívoca a posição da imagem impede uma formulação genérica das equações da óptica geométrica, o que nos obriga, no caso dos sistemas não estigmáticos, a formulações aproximadas ou válidas caso a caso. Por essa razão, esse conceito é de importância fundamental no estudo da óptica geométrica.