Espelhos esféricos são sistemas ópticos com propriedades reflexivas que podem ampliar ou diminuir as imagens, como no caso dos retrovisores dos carros. Eles podem ser côncavos ou convexos a depender da face pela qual optamos na esfera.
Dependendo da posição à frente do espelho côncavo, podemos obter diversos tipos de imagens, cujas características podem ser invertida (virada para baixo) ou direita (virada para cima), virtual (formada pelo prolongamento dos raios de luz) ou real (formada pelos raios de luz) e maior, menor ou igual ao tamanho do objeto.
Veja também: Espelhos planos — as superfícies que refletem a luz de forma regular
Tópicos deste artigo
- 1 - Resumo sobre espelhos esféricos
- 2 - O que são espelhos esféricos?
- 3 - Elementos dos espelhos esféricos
- 4 - Características das imagens
- 5 - Tipos de espelhos esféricos
- 6 - Fórmulas dos espelhos esféricos
- 7 - Exercícios resolvidos sobre espelhos esféricos
Resumo sobre espelhos esféricos
-
Usamos os espelhos para vermos nosso reflexo ou objetos atrás de nós.
-
Os espelhos esféricos podem ser côncavos ou convexos.
-
O foco no espelho côncavo é positivo. Já no espelho convexo, o foco é negativo.
-
As imagens podem ser reais ou virtuais; maiores, menores ou iguais ao tamanho do objeto; direitas ou invertidas.
-
A formação das imagens depende do tipo de espelho: nos convexos, há cinco tipos de imagens; nos côncavos, todas as imagens formadas são iguais.
O que são espelhos esféricos?
Espelhos esféricos são superfícies esféricas lisas e polidas, compostas de vidro transparente e comumente envolvidas por uma película de prata, que podem refletir os raios de luz vindos de diferentes ângulos de incidência. São amplamente utilizados em nosso cotidiano, seja para vermos nosso reflexo ou para observamos objetos atrás de nós, como no caso dos retrovisores.
Elementos dos espelhos esféricos
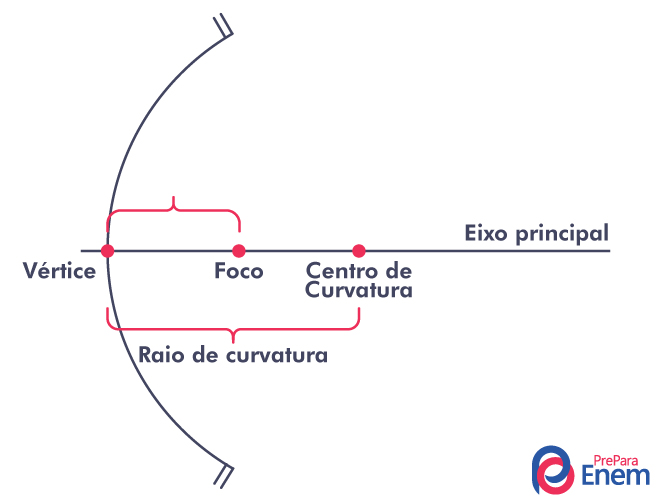
Existem alguns elementos geométricos comuns a todos os tipos de espelhos. São eles:
-
Eixo principal ou eixo de simetria (\({E}_{p}\)): linha imaginária que contém os elementos geométricos das lentes.
-
Centro de curvatura (C): ponto no centro da esfera que dá origem ao espelho, portanto a distância do espelho até esse ponto forma o raio dessa esfera. Raios incididos sobre o centro de curvatura são refletidos sobre si mesmo.
-
Foco (F): nos espelhos côncavos, é o ponto onde os raios convergem após a reflexão, sendo um foco real e representado pelo sinal positivo. Já nos espelhos convexos, é o ponto atrás do espelho onde ocorre o cruzamento dos raios refletidos que foram divergidos (prolongamentos dos raios de luz), causando um foco virtual, que representamos pelo sinal negativo.
-
Vértice (V): é o ponto no centro do espelho. Podemos considerar que a sua esquerda é o mundo real e a sua direita o mundo virtual, o reflexo.
-
Raio de curvatura (R): é a distância do vértice ao centro de curvatura.
-
Distância focal (\({f}\)): é a distância do foco até o vértice
-
Ângulo de abertura: é o grau de curvatura do espelho.
Além dos elementos que estão presentes no eixo principal, temos os elementos usados para referenciar o objeto e a imagem, sendo eles:
-
Posição do objeto no eixo principal (\(p_o\)).
-
Posição da imagem no eixo principal (\(p_i\)).
-
Altura do objeto (o).
-
Altura da imagem (i).
Saiba mais: Lentes esféricas — um sistema óptico que refrata a luz visível
Características das imagens
-
Imagem real: A imagem do objeto pode ser real quando é formada pelos raios de luz, sendo sua imagem produzida à frente do espelho.
-
Imagem virtual: A imagem do objeto pode ser virtual quando é formada pelo prolongamento dos raios, sendo sua imagem produzida “atrás” do espelho.
-
Imagem direita: A imagem pode ser direita quando estiver no mesmo sentido do objeto.
-
Imagem invertida: A imagem pode ser invertida quando estiver no sentido contrário ao objeto.
Importante: Há também o fato de que a imagem pode ser maior, igual ou menor ao objeto colocado em frente ao espelho (tamanho real).
Tipos de espelhos esféricos
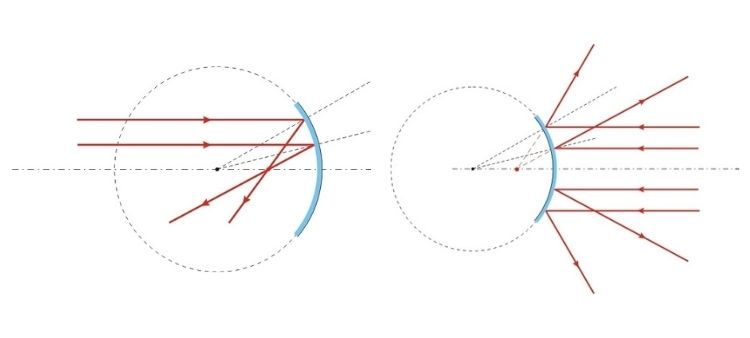
Os espelhos esféricos são divididos em dois tipos, que são obtidos dependendo da face que selecionamos na esfera.
-
Espelhos côncavos
Nos espelhos côncavos, a face refletiva é a interna. Os espelhos côncavos são muito utilizados na formação de imagens virtuais e ampliadas dos objetos situados próximos a ele. São os espelhos que usamos na aplicação de maquiagem ou para remoção de acnes. Dependendo da localização do objeto no eixo principal, obtemos ou não uma imagem.
-
Objeto localizado antes do foco \(F\)
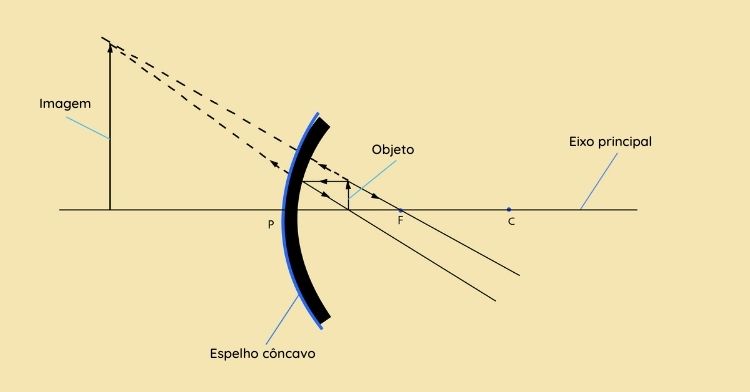
-
Objeto localizado no foco \(F\)
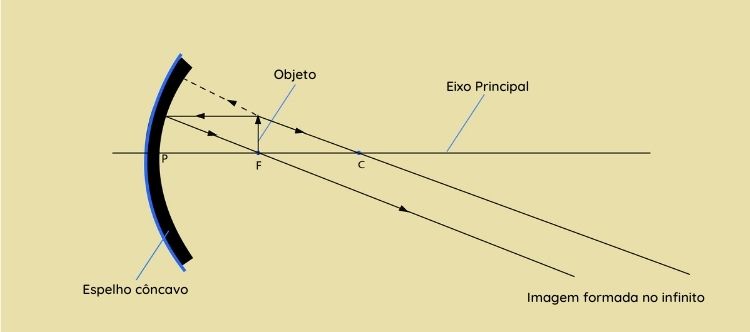
-
III. Objeto localizado entre o foco \(F\) e o centro de curvatura \(C\)
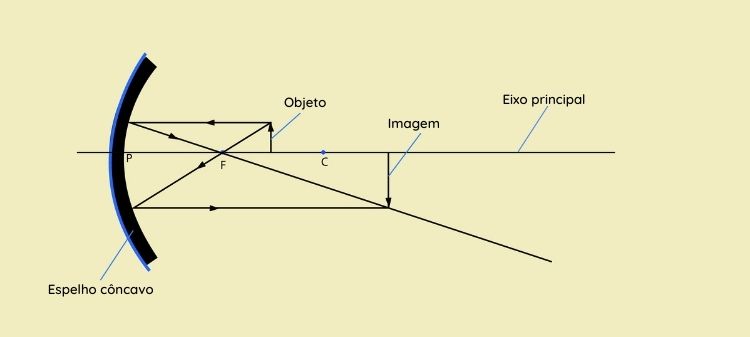
-
Objeto localizado no centro de curvatura C
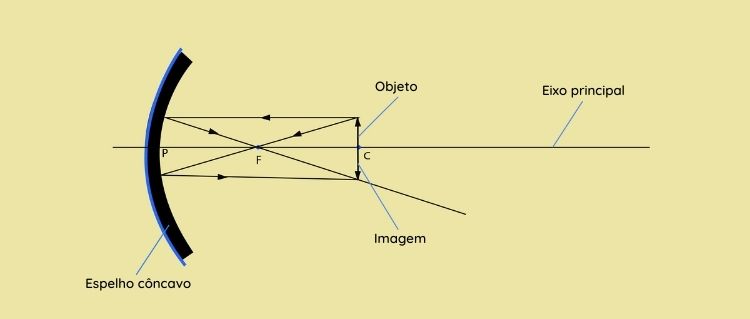
-
Objeto localizado depois do centro de curvatura C
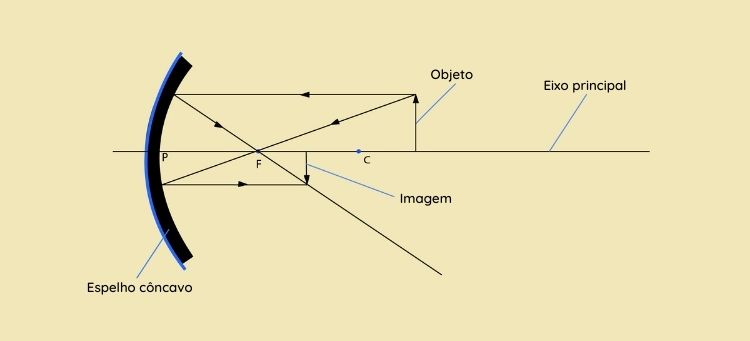
-
Videoaula sobre espelhos esféricos côncavos
-
Espelhos convexos
Nos espelhos convexos, a face refletida é a externa. Os espelhos convexos são muito utilizados na formação de imagens ampliadas dos objetos, independentemente da sua localização. São usados em estabelecimentos comerciais e no transporte coletivo.
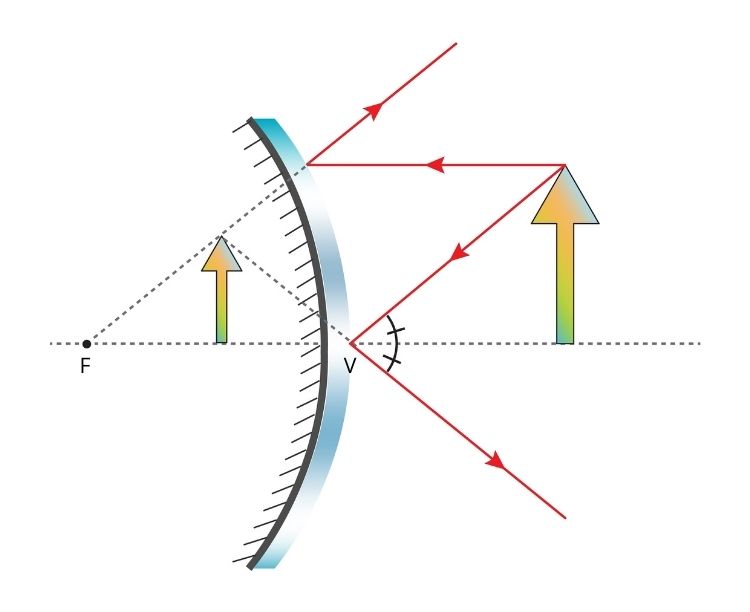
-
Videoaula sobre espelhos esféricos convexos
Fórmulas dos espelhos esféricos
As fórmulas para espelhos côncavos e convexos são as mesmas, com exceção do foco, que é positivo para o espelho côncavo e negativo para o espelho convexo.
Vale ressaltar que em espelhos esféricos utilizamos o referencial de Gauss, uma vez que ele possibilita saber as posições das imagens e sua nitidez.
-
Recebem sinal positivo: objetos ou imagens localizados à frente do espelho e objetos ou imagens direitos.
-
Recebem sinal negativo: objetos ou imagens localizados atrás do espelho e objetos ou imagens invertidos.
Tendo isso em vista, observe as fórmulas dos espelhos esféricos abaixo.
→ Distância focal e raio de curvatura
\(f=\frac{R}{2}\)
-
\({f}\) é a distância focal, expressa em metros \([m]\).
-
\({R}\) é o raio de curvatura, expresso em metros \( [m]\).
→ Equação dos pontos conjugados
\(\frac{1}{f}=\frac{1}{p_o}+\frac{1}{p_i}\)
-
\({p}_{o}\) é a distância do foco ao objeto, ou posição do objeto.
-
\({p}_{i}\) é a distância do foco à imagem, ou posição da imagem.
→ Equação do aumento linear transversal
\(A=\frac{i}{o}=\frac{-\ p_i}{p_o}=\frac{f}{f-p_o}\)
-
A é o aumento linear transversal. Quando seu resultado é positivo, significa que a imagem é virtual e direita. Se for negativo, a imagem é real e invertida.
Leia também: Outros tipos de espelhos utilizados no dia a dia
Exercícios resolvidos sobre espelhos esféricos
Questão 1
(Unespar) Considere um espelho esférico côncavo e um objeto colocado entre o foco F e o centro de curvatura C. Considere as características de imagens nas afirmativas a seguir:
I. Imagem real e menor que o objeto.
II. Imagem virtual e maior que o objeto.
III. Imagem real e maior que o objeto.
IV. Imagem de cabeça para baixo.
V. Imagem sem estar de cabeça para baixo.
Assinale a alternativa correta com relação à imagem que será formada:
A) As afirmativas I e IV estão corretas.
B) As afirmativas II e V estão corretas.
C) As afirmativas III e IV estão corretas.
D) As afirmativas II e IV estão corretas.
E) Todas as afirmativas estão corretas.
Resolução:
Alternativa C
Quando temos um objeto colocado entre o foco e o centro de curvatura, a imagem que obtemos é real, invertida e maior que o objeto.
Questão 2
(Udesc) Um lápis foi colocado a 30,0 cm diante de um espelho esférico convexo de distância focal igual a 50,0 cm, perpendicularmente ao eixo principal. O lápis possui 10,0 cm de comprimento. Com base nessas informações, pode-se afirmar que a posição e o tamanho da imagem do lápis são, respectivamente:
A) 75,0 cm e -25,0 cm.
B) 18,75 mm e -6,25 mm.
C) -75,0 cm e 25,0 cm.
D) 75,0 cm e 6,25 cm.
E) -18,75 cm e 6,25 cm.
Resolução:
Alternativa E
No enunciado, temos que a distância focal é 50 cm, mas como se trata de um espelho convexo, o foco é negativo. Assim, a distância focal na verdade é -50 cm. O comprimento do lápis é 10 cm, e a distância do objeto ao espelho ou posição do objeto é 30 cm. Primeiramente, calcularemos a posição da imagem utilizando a equação dos pontos conjugados:
\(\frac{1}{f}=\frac{1}{p_o}+\frac{1}{p_i}\)
\(\frac{1}{-50}=\frac{1}{30}+\frac{1}{p_i}\)
\(-\frac{1}{50}-\frac{1}{30}=\frac{1}{p_i}\)
\(\frac{-3-5}{150}=\frac{1}{p_i}\)
\(\frac{-8}{150}=\frac{1}{p_i}\)
\(-8\bullet p_i=150\)
\(p_i=\frac{150}{-8}\)
\(p_i=-18,75\ cm\)
Já o tamanho da imagem, calcularemos pela equação do aumento linear transversal:
\(\frac{i}{o}=\frac{-\ p_i}{p_o}\)
\(\frac{i}{10}=\frac{-\ (-18,75)}{30}\)
\(30\bullet i=187,5\)
\(i=\frac{187,5}{30}\)
\(i=6,25\ cm\)
Crédito de imagem
[1] Danny Ye / Shutterstock







