É necessário que no estudo da Hidrostática algumas condições iniciais sejam estabelecidas. Por exemplo, se estudarmos um fluido na forma como ele realmente se apresenta, teremos um sistema mais complexo. Assim, é melhor considerar um fluido que, além de satisfazer algumas condições, apresente comportamento semelhante ao comportamento de um fluido ideal. Dessa forma, podemos dizer que o fluido de nosso estudo possui densidade constante, e sua velocidade de escoamento, em um ponto qualquer, também é constante em relação ao tempo.
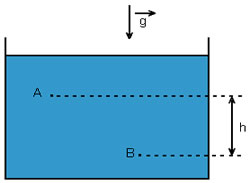
Vamos supor então um fluido ideal escoando (escorrendo) no interior de um tubo que sofre uma redução de área, como mostra a figura acima. Podemos ver pela figura que entre os pontos A e B não há perda ou ganho de fluido por meio de ramificações. Dessa forma, podemos afirmar que entre esses pontos o fluido não entra e nem sai. Portanto, em relação ao sentido de escoamento do fluido (da esquerda para a direita), em um intervalo de tempo, o volume do fluido que passa em A é o mesmo volume que passa em B. Diante disso, podemos escrever o seguinte:
∆vA= ∆vB
Em virtude de as regiões A e B possuírem diâmetros diferentes, o volume de fluido em A (∆vA) é dado pelo produto da área A1 pela distância d1; e em B (∆vB) é dado pelo produto da área A2 pela distância d2. A equação acima pode ser escrita da seguinte forma:
A1.d1= A2.d2 (I)
Lembrando que em cada região a velocidade de escoamento do fluido é constante, temos que:
d1= v1.∆t e d2= v2.∆t
Substituindo as expressões anteriores em I, temos:
A1.v1.∆t= A2.v_2.∆t
A1.v1= A2.v2
Essa expressão recebe o nome de equação de continuidade. A partir dessa equação podemos dizer que, em qualquer ponto do escoamento do fluido, o produto da velocidade de escoamento pela área do tubo é constante; consequentemente, nas partes mais estreitas do tubo, ou seja, na menor área, a velocidade de escoamento é maior.
O produto v.A, que no SI é dado em m3/s, recebe o nome de vazão (Q):
Q= v.A