A energia potencial gravitacional é a forma de energia potencial que ocorre devido à variação de altura sofrida por um corpo, sendo calculada pela multiplicação da massa do corpo, a aceleração da gravidade e a altura da localização do corpo.
Tópicos deste artigo
- 1 - Resumo sobre energia potencial gravitacional
- 2 - O que é energia potencial gravitacional?
- 3 - Alguns exemplos de energia potencial gravitacional
- 4 - Qual a fórmula da energia potencial gravitacional?
- 5 - Transformação da energia potencial gravitacional
- 6 - Energia potencial gravitacional x energia potencial elástica
- 7 - Exercícios resolvidos sobre energia potencial gravitacional
Resumo sobre energia potencial gravitacional
A energia potencial gravitacional é a forma de energia potencial associada à altura dos corpos.
Sempre que partimos do ponto mais baixo para o ponto mais alto, a energia potencial gravitacional aumenta.
A energia potencial gravitacional é calculada pelo produto entre a massa de um corpo, a aceleração da gravidade e a altura de onde ele está.
A energia potencial gravitacional pode ser transformada em outras formas de energia, como a cinética e a potencial elástica.
Enquanto a energia potencial gravitacional é a forma de energia potencial que ocorre devido às variações de altura de um corpo, a energia potencial elástica é a forma de energia potencial que ocorre devido à deformação elástica de um corpo.
O que é energia potencial gravitacional?
A energia potencial gravitacional é uma grandeza física escalar relacionada à posição de um corpo em relação a uma região dotada de campo gravitacional. De acordo com o Sistema Internacional de Unidades, a unidade de medida da energia potencial gravitacional é o Joule, representado pela letra J.
Alguns exemplos de energia potencial gravitacional
Existem diversos exemplos da energia potencial gravitacional em nosso cotidiano, pensando nisso, selecionamos abaixo alguns exemplos:
- Quando subimos por elevador, escadas ou escadas rolantes.
- Quando brincamos de pular corda.
- Quando pulamos nos trampolins, sofás e camas.
- Quando lançamos um objeto para o alto.
- Quando os automóveis sobem uma colina.
- Quando um corpo está no alto de um plano inclinado.
Qual a fórmula da energia potencial gravitacional?
\({E}_{\text{pg}} = m \cdot g \cdot h \)
- \({E}_{\text{pg}} \) → energia potencial gravitacional, medida em Joule [J].
- m → massa, medida em quilograma [kg].
- g → aceleração da gravidade, vale aproximadamente \(9,8 m/s².\)
- h → altura, medida em metros [m].
Exemplo:
Calcule a energia potencial gravitacional em um corpo de 45Kg a 10 m do solo, considerando que a aceleração da gravidade local é de \(9,8 m/s².\)
Resolução:
Calcularemos a energia potencial gravitacional por meio da sua fórmula:
\({E}_{\text{pg}} = m \cdot g \cdot h \)
\({E}_{\text{pg}} = 45 \cdot 9.8 \cdot 10 \)
\({E_pg} =4410 J\)
Portanto, a energia potencial gravitacional nesse corpo é de 4410 J.
Transformação da energia potencial gravitacional
A energia potencial gravitacional pode ser transformada em outras formas de energia, como energia cinética e energia potencial elástica, devido ao princípio de conservação da energia, no qual uma energia pode ser convertida na outra, mas jamais criada ou destruída. Por exemplo, quando um objeto escorrega ou cai de certa altura, a sua energia potencial gravitacional é convertida em energia cinética, provocando o seu movimento, como na imagem abaixo:
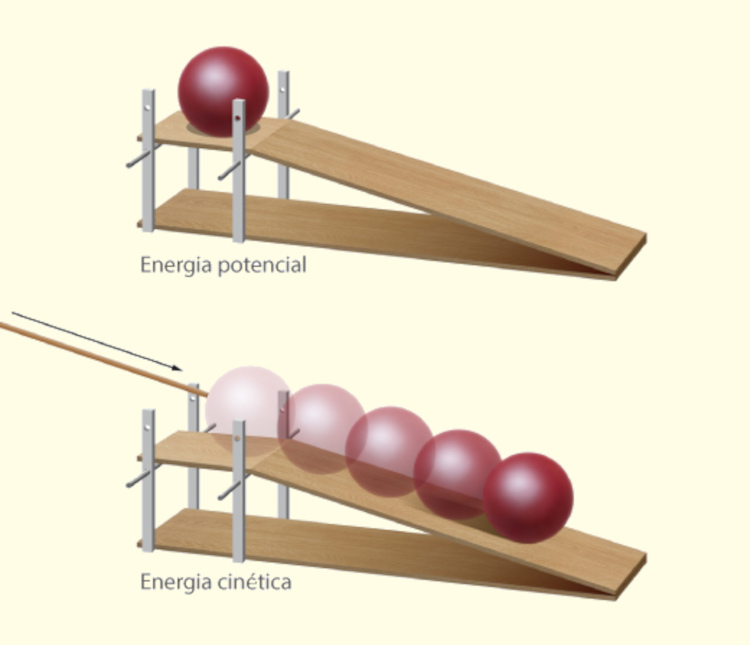
Energia potencial gravitacional x energia potencial elástica
A energia potencial gravitacional e a energia potencial elástica são tipos de energia potencial com características bem distintas.
- Energia potencial gravitacional: é a energia em um corpo devido à variação de sua altitude, sendo calculada pela fórmula:
\({E}_{\text{pg}} = m \cdot g \cdot h \)
- \({E}_{\text{pg}}\) → energia potencial gravitacional, medida em Joule [J].
- m → massa, medida em quilograma [kg].
- g → aceleração da gravidade, vale aproximadamente \(9,8 {m} / {{s} ^ {2}}\).
- h → altura, medida em metros [m].
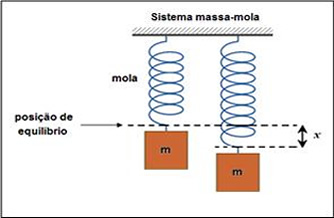
- Energia potencial elástica: é a energia em um corpo devido a sua capacidade de se deformar elasticamente, sendo calculada pela fórmula:
\({E}_{\text{pel}} = \frac{k \cdot {x}^2}{2} \)
- \({E}_{\text{pel}}\) → energia potencial elástica, medida em Joule [J].
- k → constante elástica, medida em [N/m].
- x → deformação do objeto, medida em metros [m].
Para saber mais sobre a energia potencial elástica, clique aqui.
Exercícios resolvidos sobre energia potencial gravitacional
Questão 1
(Fatec) Um bloco de massa 0,60 kg é abandonado, a partir do repouso, no ponto A de uma pista no plano vertical. O ponto A está a 2,0 m de altura da base da pista, onde está fixa uma mola de constante elástica 150 N/m. São desprezíveis os efeitos do atrito e adota-se g = 10 m/s². A máxima compressão da mola vale, em metros:
A) 0,80
B) 0,40
C) 0,20
D) 0,10
E) 0,05
Resolução:
Alternativa B
Calcularemos a máxima compressão da mola transformando a energia potencial gravitacional em energia potencial elástica, e igualando suas fórmulas:
\({E}_{\text{pg}} = {E}_{\text{pel}} \)
\(m \cdot g \cdot h = \frac{k \cdot {x}^2}{2} \)
\(0,6 \cdot 10 \cdot 2 = \frac{150 \cdot {x}^2}{2} \)
\(12 = 75 \cdot {x}^2 \)
\({x}^2 = \frac{12}{75} \)
\({x} ^ {2} =0,16\)
\(x= \sqrt {0,16}\)
\(x=0,4 m\)
Questão 2
(IFSP) Um atleta de salto com vara, durante sua corrida para transpor o obstáculo à sua frente, transforma a sua energia _____________ em energia ____________ devido ao ganho de altura e consequentemente ao/à _____________ de sua velocidade.
As lacunas do texto acima são, correta e respectivamente, preenchidas por:
A) potencial – cinética – aumento.
B) térmica – potencial – diminuição.
C) cinética – potencial – diminuição.
D) cinética – térmica – aumento.
E) térmica – cinética – aumento.
Resolução:
Alternativa C
Um atleta de salto com vara, durante sua corrida para transpor o obstáculo à sua frente, transforma a sua energia cinética em energia potencial devido ao ganho de altura e, consequentemente, ao/à diminuição de sua velocidade.
Fontes
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Mecânica. 8. ed. Rio de Janeiro, RJ: LTC, 2009.
NUSSENZVEIG, Herch Moysés. Curso de física básica: Mecânica (vol. 1). 5 ed. São Paulo: Editora Blucher, 2015.