Energia potencial elétrica

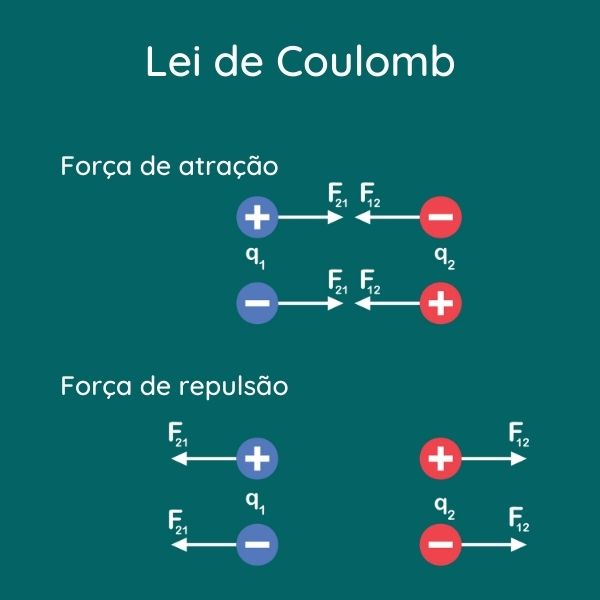
A energia potencial elétrica é a energia associada à interação entre, pelo menos, dois corpos com cargas elétricas. Para que ela ocorra, é necessário mais de um corpo carregado, porém, quando apenas um corpo carregado está em um meio, ele produz um campo elétrico e um potencial elétrico, em uma área em torno de si, que afetarão qualquer corpo introduzido nas imediações.

No capacitor, a energia potencial elétrica está associada à capacitância e à tensão formada entre os condutores que o compõem. Quando a segunda carga se move, aproximando-se ou se afastando da carga elétrica principal, a energia potencial sofre uma variação, tal variação é chamada de trabalho da força elétrica, já que a atração ou a repulsão se devem à lei de Coulomb.

Leia também: Como o conteúdo que envolve eletricidade é cobrado no Enem?

Tópicos deste artigo

• 1 - Resumo sobre energia potencial elétrica
• 2 - O que é energia potencial elétrica?
• 3 - Qual a fórmula da energia potencial elétrica?
• 4 - Potencial elétrico x energia potencial elétrica
• 5 - Energia potencial elétrica no capacitor
• 6 - Variação da energia potencial elétrica
• 7 - Energia potencial elétrica x energia elétrica
• 8 - Exercícios resolvidos sobre energia potencial elétrica

Resumo sobre energia potencial elétrica

• Energia potencial elétrica é a energia que possibilita o movimento de um corpo eletricamente carregado devido à influência da carga presente em outro corpo fixo.
• O potencial elétrico está relacionado com a energia necessária para mover uma unidade de carga elétrica de um ponto a outro.
• A energia potencial elétrica de um capacitor refere-se ao trabalho necessário para armazenar as cargas entre seus condutores.
• A energia elétrica é o trabalho realizado pela corrente elétrica para fazer com que o receptor funcione.
• A grandeza relacionada com a variação da energia potencial elétrica é o trabalho.

O que é energia potencial elétrica?

A energia potencial elétrica é a energia resultante da interação entre, pelo menos, dois corpos eletricamente carregados e separados por uma distância. Quando um corpo com carga elétrica não nula (corpo primário) está em um meio, ele gera um campo elétrico em sua volta, e qualquer corpo, também carregado (corpo secundário), que entrar nesse campo será atraído (corpos com cargas de sinais diferentes) ou repelido (corpos com cargas de mesmo sinal) devido à lei de Coulomb (força elétrica).

Quanto maiores as cargas dos corpos, maior será a energia potencial elétrica, em contrapartida, quanto maior a distância que os separa, menor será a interação entre eles e, consequentemente, menor será a energia potencial. Quando essa interação ocorre, o corpo secundário entra em movimento, sendo atraído ou repelido, logo, a energia potencial elétrica é convertida em energia cinética, e esta, por sua vez, será convertida em outro tipo de energia ou dissipada.

A energia potencial elétrica, por se tratar de um tipo de energia, é uma grandeza escalar, consequentemente, pode ser positiva ou negativa, isso dependerá do sinal da carga dos corpos que comporão o sistema e também do referencial adotado nos cálculos.

Leia também: Eletrostática — ramo que estuda os fenômenos associados às cargas elétricas em repouso

Qual a fórmula da energia potencial elétrica?

A energia potencial elétrica E_pe (em joule J) é diretamente proporcional ao valor das cargas Q e q (em coulomb C) dos corpos envolvidos e à constante eletrostática do meio K (no caso do vácuo, 9·10⁹ N.m²/C²), e inversamente proporcional à distância d (em metros) entre os corpos.

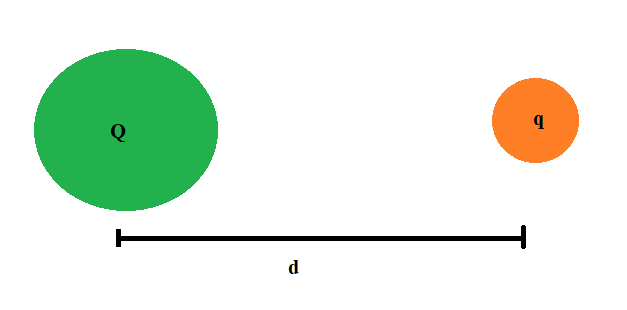
\(E_{pe}=\frac{K\cdot Q\cdot q}{d}\)

Exemplo:

Um corpo que possui carga de 12μC foi inserido em uma região com constante eletrostática similar à do vácuo. A 1,5 metro do primeiro corpo, foi inserida uma carga de prova de 2μC. Qual a energia potencial elétrica resultante dessa interação?

Resposta:

Extraindo os dados:

• Q = 12μC = 12·10^-6 C
• K = 9·10⁹ N.m²/C²
• q = 2μC = 2·10^-6 C
• d = 1,5 m
• Epe = ?

\(E_{pe}=\frac{K\cdot Q\cdot q}{d}=\frac{9\cdot{10}^9\cdot12\cdot{10}^{-6}\cdot2\cdot{10}^{-6}}{1,5}\)

\(E_{pe}=\frac{216\cdot{10}^{9+\left(-6\right)+\left(-6\right)}}{1,5}=\frac{216\cdot{10}^{-3}}{1,5}=144\cdot{10}^{-3}\)

Convertendo para notação científica:

\(E_{pe}=1,44\cdot{10}^{-1}J\)

Potencial elétrico x energia potencial elétrica

Enquanto a energia potencial elétrica é a energia associada pela interação entre dois corpos carregados, o potencial elétrico V (medido em volts, também representado por V) é a energia associada para transportar uma unidade de carga de um ponto a outro.

Dessa forma, o potencial elétrico é uma grandeza associada à existência de um corpo carregado em determinada região, e a energia potencial surge quando um segundo corpo carregado é inserido nessa região. O potencial elétrico V é representado pela equação abaixo.

\(V=\frac{K\cdot Q}{d}\)

Associando o potencial elétrico com a energia potencial elétrica, obtém-se a equação a seguir.

\(E_{pe}=V\cdot q\)

Exemplo:

Uma energia potencial elétrica de 1,6·10^-3 J é gerada quando uma carga de prova de 4nC foi inserida em determinado potencial elétrico. Qual foi o valor desse potencial?

Resposta:

Extraindo os dados:

• E_pe = 1,6·10^-3 J
• q = 4nC = 4·10^-9 C
• V = ?

\(E_{pe}=V\cdot q\)

\(1,6\cdot{10}^{-3}=V\cdot4\cdot{10}^{-9}\)

Invertendo os lados da equação:

\(V\cdot4\cdot{10}^{-9}=1,6\cdot{10}^{-3}\)

Isolando o potencial:

\(V=\frac{1,6\cdot{10}^{-3}}{4\cdot{10}^{-9}}=0,4\cdot{10}^{-3-\left(-9\right)}=0,4\cdot{10}^6\)

Convertendo em notação científica:

\(V=4\cdot{10}^5V\)

Energia potencial elétrica no capacitor

Um capacitor é um dispositivo que tem como finalidade armazenar carga elétrica entre dois condutores paralelos separados por um dielétrico (isolante). Cada condutor possui um potencial elétrico. A diferença entre os potenciais de cada condutor é representada por U (medido em volts V). Dessa forma, pela presença das cargas, resulta-se em uma energia potencial elétrica que, em termos da capacitância C (medida em faraday F), pode ser descrita pela equação a seguir:

\(E_{pe}=\frac{C\cdot U^2}{2}\)

\(U=V_A-V_B\)

Em termos da carga armazenada Q, a equação pode ser reescrita de outra forma:

\(E_{pe}=\frac{Q\cdot U}{2}\)

Exemplo:

Um capacitor de placas paralelas possui uma diferença de potencial igual a 15 V entre suas placas. Após ser carregado, a energia potencial elétrica resultante da presença de uma carga nele é de 45 J. Calcule o valor da capacitância desse capacitor.

Resposta:

Extraindo os dados do problema:

• U = 15 V
• Epe = 45 J
• C = ?

\(E_{pe}=\frac{C.U^2}{2}\)

\(45=\frac{C\cdot{15}^2}{2}\)

O 2 passa multiplicando o 45, e resolve-se a potenciação:

\(90=C\cdot225\)

Inverte-se os lados da operação:

\(C\cdot225=90\)

\(C=\frac{90}{225}=0,4\ F\)

Variação da energia potencial elétrica

A variação da energia potencial elétrica ocorre quando a carga secundária se move. Caso ela seja atraída, a variação entre a energia inicial e final será positiva; caso seja repelida, será negativa, já que a energia potencial é inversamente proporcional à distância entre as cargas principais e secundárias. De acordo com a mecânica clássica, a variação de energia é o trabalho T, que, consequentemente, também é medido em joules.

T = ∆E_pe = E_peA - E_peB

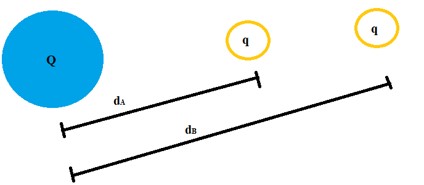
Aplicando a fórmula da energia potencial para a posição em A e para a posição em B, a equação do trabalho ficará desta maneira:

\(T=K\cdot Q\cdot q\cdot\left(\frac{1}{d_A}-\frac{1}{d_B}\right)\)

Exemplo:

Um corpo com carga de 8 C é inserido em um vácuo simulado, e uma carga de -2 C é colocada a 0,4 m dele. Após isso, a segunda carga foi atraída pela primeira. Com essas informações, calcule o trabalho realizado pelo deslocamento da carga até ela chegar a 0,1 m de distância do primeiro corpo.

Resposta:

Extraindo os dados do problema:

• Q = 8 C
• q = -2 C
• K = 9·10⁹ N.m²/C²
• d_A = 0,4 m
• d_B = 0,1 m
• T = ?

\(T=K\cdot Q\cdot q\cdot\left(\frac{1}{d_A}-\frac{1}{d_B}\right)=9\cdot{10}^9\cdot8\cdot\left(-2\right)\cdot\left(\frac{1}{0,4}-\frac{1}{0,1}\right)\)

Como se tem uma subtração entre duas frações, o denominador resultante será o produto entre os denominadores iniciais, e os numeradores são os denominadores iniciais invertidos.

\(T=-144\cdot{10}^9\cdot\left(\frac{0,1-0,4}{0,04}\right)=-144\cdot{10}^9\cdot\left(\frac{-0,3}{0,04}\right)\)

Temos dois sinais negativos multiplicando, logo, o resultante será positivo.

\(T=\frac{43,2\cdot{10}^9}{0,04}=1080\cdot{10}^9\)

\(T=1,08\cdot{10}^{12}J\)

Energia potencial elétrica x energia elétrica

A energia potencial elétrica está associada ao movimento de uma carga entre dois potenciais distintos, ou seja, ao trabalho para movimentar-se um corpo carregado do ponto A ao B, sem nenhum condutor. Por sua vez, a energia elétrica é a corrente elétrica, indo de um potencial a outro, no qual ela será convertida em um outro tipo de energia para executar um trabalho. Para que a energia elétrica ocorra, são necessários um condutor e um receptor, que a transformará em um outro tipo de energia.

Leia também: Efeito joule — o aquecimento dos materiais quando atravessados por uma corrente elétrica

Exercícios resolvidos sobre energia potencial elétrica

Questão 1

Uma carga de 20nC foi colocada em um ambiente que simula o vácuo, e, a 0,2 metros dela, foi colocada uma carga de prova de 0,5nC e 4·10^-7 kg que começou a se mover imediatamente. Qual será a velocidade da carga quando ela chegar a 0,6 m do primeiro corpo?

a) 5 m/s

b) 60 m/s

c) 2 m/s

d) 0,1 m/s

e) 10 m/s

Resposta: letra C

• K = 9·10⁹ N.m²/C²
• Q = 20nC = 20·10^-9 C
• q = 0,5nC = 0,5·10^-9 C
• m_q = 1,5·10^-7 kg
• d_A = 0,2 m
• d_B = 0,6 m
• v = ?

Pelo teorema trabalho-energia, o trabalho é tanto a variação da energia potencial elétrica como a variação da energia cinética.

\(T=\ E_{peA}-E_{peB}\)

\(T=\ E_{cB}-E_{cA}\)

Porém, no ponto A, no início a carga foi colocada, logo, não possuía velocidade inicial, restando apenas a energia no ponto B. Primeiro calcula-se a variação da energia potencial elétrica.

\(T=K\cdot Q\cdot q\cdot\left(\frac{1}{d_A}-\frac{1}{d_B}\right)=9\cdot{10}^9\cdot20\cdot{10}^{-9}\cdot0,5\cdot{10}^{-9}\cdot\left(\frac{1}{0,2}-\frac{1}{0,6}\right)\)

\(T=90\cdot{10}^{-9}\cdot\left(\frac{0,6-0,2}{0,12}\right)=90\cdot{10}^{-9}\cdot\left(\frac{0,4}{0,12}\right)=\frac{36\cdot{10}^{-9}}{0,12}\)

\(T=300\cdot{10}^{-9}=3\cdot{10}^{-\ldots7}J\)

Se T_{potencial elétrica} = T_cinética:

\(T=3\cdot{10}^{-7}=E_{cB}=\frac{m\cdot v^2}{2}\)

\(3\cdot{10}^{-7}=\frac{1,5\cdot{10}^{-7}\cdot v^2}{2}\)

\({6\cdot10}^{-7}=1,5\cdot{10}^{-7}\cdot v²\)

Invertendo a equação:

\(1,5\cdot{10}^{-7}\cdot v^2={6\cdot10}^{-7}\)

\(v^2=\frac{{6\cdot10}^{-7}}{1,5\cdot{10}^{-7}}=4\)

\(v^2=4\)

Como a incógnita está elevada ao quadrado, é necessário acrescentar raiz quadrada nos dois lados da equação para eliminar o expoente.

\(\sqrt{v^2}=\sqrt4\)

\(v=2\ m/s\)

Questão 2

Leia as afirmações a seguir:

I) A energia potencial elétrica pode ocorrer quando um corpo eletricamente carregado está sozinho em um meio.

II) A energia elétrica é o resultado do deslocamento da corrente elétrica em um circuito fechado para fazer com que um receptor execute determinado trabalho.

III) A variação da energia potencial elétrica equivale ao trabalho necessário para deslocar um corpo eletricamente carregado.

IV) No capacitor, a presença de carga elétrica resulta em uma energia potencial elétrica entre as placas com o mesmo potencial elétrico que o constitui.

Marque a alternativa que representa corretamente a classificação das afirmações em verdadeiras e falsas.

a) FVVF

b) VFFV

c) VVVF

d) FVVV

e) Todas as alternativas são verdadeiras.

Resposta: letra A

I) Falsa. Para haver energia potencial elétrica, é necessário a existência de, pelo menos, dois corpos eletricamente carregados.

II) Verdadeira

III) Verdadeira.

IV) Falsa. No capacitor, os potenciais das placas que o constituem devem ser diferentes.