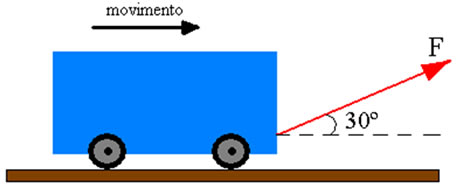
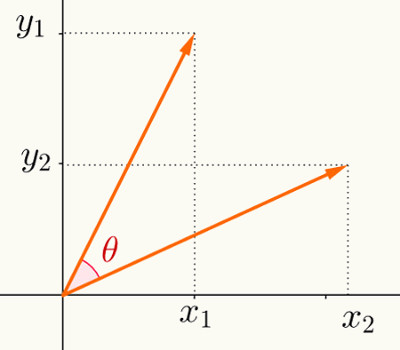Veja a figura acima, nela temos um bloco sendo puxado por uma força oblíqua de intensidade F. Como efeito dessa força podemos obter dois resultados por conta da ação dessa força F. Há momentos em que podemos observar o objeto se deslocando tanto na horizontal quanto na vertical. Nesse tipo de situação apenas uma única força pode estar produzindo esses dois efeitos.
Dizemos então que cada um desses efeitos está sendo provocado por uma pequena parte da força aplicada no corpo. Na física, chamamos essa pequena parte de componente. Então vamos aprender a determinar essas componentes.
Na física costumamos dizer que qualquer tipo de grandeza vetorial pode ser decomposta. Essa decomposição é realizada no plano cartesiano como referencial de orientação. Veja a figura abaixo onde temos um vetor v que se origina no ponto de origem do plano cartesiano.

Perceba que o vetor velocidade é inclinado, isto é, é um vetor que forma um ângulo em relação ao eixo x do plano cartesiano. Se traçarmos uma linha paralela a y e que corta o eixo x teremos a projeção horizontal do vetor v na direção x, e se traçarmos uma linha paralela a x e que corta o eixo y teremos a projeção vertical do vetor v na direção y. Sendo assim, temos:

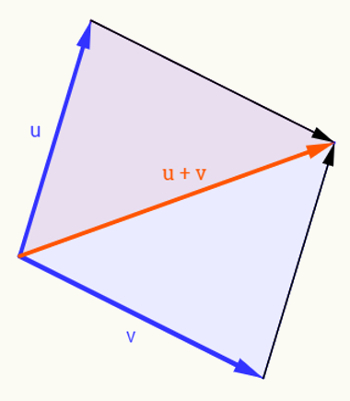
Pela regra do paralelogramo, a soma vetorial dos vetores ortogonais Vx e Vy nos fornece como resultado o próprio vetor V. Desta forma, podemos concluir que:

Podemos concluir com esse estudo que decompor um vetor significa determinar suas componentes na direção x e na direção y. Para calcular o valor do módulo desses componentes basta fazer uso do seno e cosseno, e a partir do triângulo retângulo formado na figura, obter as seguintes equações:
vx = v.cosθ e vy = v.senθ