Conservação da energia mecânica

Desde os primeiros estudos sobre um sistema físico, sabemos que a energia mecânica pode ser modificada, mas nada dela se perde. Por vários anos, diversos trabalhos, nas mais variadas áreas, direcionaram para a formulação de uma lei fundamental denominada lei da conservação da energia. Quando ela é encarada como um dos pilares da construção do universo, referimo-nos a ela como Princípio da Conservação da Energia.

Voltemos às forças conservativas: elas foram assim denominadas por causa dessa lei. Sistemas em que apenas as forças conservativas realizam trabalho conservam a energia mecânica (observe que o sistema pode apresentar outras forças, desde que elas não realizem trabalho).

No estudo da mecânica, as forças gravitacional e elástica são caracterizadas como sendo forças conservativas. Então, sistemas nos quais apenas essas duas forças realizam trabalho apresentam a energia mecânica inicial igual à energia mecânica final. Vejamos alguns exemplos:

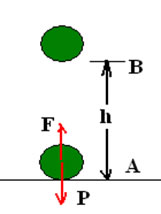
Suponhamos que temos um ponto material, e que esse ponto material seja lançado para cima, em uma região de vácuo, na superfície da Terra. No decorrer de sua subida, a energia potencial desse ponto material aumenta, enquanto que sua energia cinética diminui de tal forma que a soma entre essas duas energias seja sempre constante. Ao descer, a energia potencial é gradualmente transformada em energia cinética.

Já em um sistema massa-mola sem atrito, quando o bloco é deslocado do ponto de referência (O) e depois abandonado, verificamos a conservação da energia mecânica em qualquer ponto durante seu movimento oscilatório.

Se houver trabalho de forças não conservativas, a energia mecânica não se conservará, isto é, ela pode diminuir ou aumentar. As forças não conservativas cujo trabalho provoca diminuição da energia mecânica são denominadas forças dissipativas. É o caso da força de atrito de escorregamento e da força de resistência do ar.

Vamos supor que um corpo em movimento possua, num ponto A, energia cinética, energia potencial gravitacional e energia elástica. Ao passar por um outro ponto, B, ele possuirá energia cinética, energia potencial gravitacional e energia potencial elástica . Se apenas forças conservativas realizarem trabalho, a lei da conservação da energia mecânica garante que:

E_cA +E_p(g)A+E_eA=E_cB+E_p(g)B +E_eB

As situações nas quais o princípio da conservação da energia mecânica é válido são ideais. Rigorosamente, elas são raríssimas. Forças dissipativas, como a resistência do ar e os atritos, são praticamente inevitáveis. Para esses sistemas, o trabalho realizado pelas forças dissipativas corresponde à diferença entre a energia mecânica final e inicial do corpo, desde que o sistema não permita a entrada de energia:

τ_Fdissipativa = E_mf - E_mi

Na equação acima temos:

τ – trabalho da força dissipativa
Em_f – energia mecânica final
Em_i – energia mecânica inicial

Aproveite para conferir as nossas videoaulas relacionadas ao  assunto: