Sempre que em uma determinada região do espaço há a ação de uma força, podemos dizer que existe também um campo, cuja natureza depende da causa que origina essa força. Por exemplo, se existe força de natureza elétrica em uma determinada região, também há nessa região um campo elétrico.
Compreendendo a noção de campo, vejamos agora como se define o campo gravitacional. Os objetos que possuem massa exercem atração sobre outros corpos que também possuem massa. Como exemplo, podemos citar a atração que a Terra exerce sobre os corpos em sua superfície, ou a atração que o Sol exerce sobre os planetas que orbitam ao seu redor.
A força que justifica esses dois fenômenos está ligada à massa desses corpos e é denominada de força gravitacional, sendo que, na região de atuação dessa força, existe o campo gravitacional.
Todos os corpos que têm massa possuem campo gravitacional, de forma que, ao colocarmos uma partícula na região de atuação desse campo, será estabelecida uma força gravitacional entre ambos.
Matematicamente, o campo gravitacional é dado pela equação:
g = P
m
Sendo:
g - o campo gravitacional;
P - força de interação graças à existência desse campo;
m – massa do corpo;
A fórmula acima pode ser reescrita da seguinte forma:
P = m.g
Essa expressão é a mesma obtida com a Segunda Lei de Newton. Isso quer dizer que a aceleração da gravidade e o campo gravitacional representam a mesma grandeza física. Porém, só podemos utilizar a expressão acima para calcular o campo gravitacional se já é conhecida a força de interação entre os corpos.
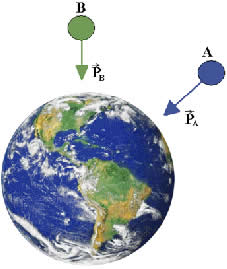
Para calcular o campo gravitacional em qualquer região do espaço, podemos utilizar a Lei da gravitação universal. Observe a figura a seguir que mostra um corpo de massa M próximo a outro corpo de massa m localizados a uma distância r um do outro.

A figura mostra a interação gravitacional entre os corpos de massa M e m
A força gravitacional entre esses dois corpos é dada pela expressão:
F = G . M .m
r2
Sendo:
G = 6,67 . 10-11, a constante de gravitação universal;
r – a distância entre os centros dos dois corpos.
Lembrando que há a equação P = m . g, em que P também representa a força gravitacional. Podemos substituir o F da equação acima por m.g, obtendo a expressão:
m.g = G . M .m
r2
Simplificando m, obtemos:
g = G . M
r2
A equação acima nos permite calcular o campo gravitacional ou a aceleração da gravidade para qualquer corpo e em qualquer região do espaço. A unidade de medida no S.I. é m/s2, a mesma utilizada para a aceleração.
O campo gravitacional é responsável por ficarmos “presos” à superfície da Terra, pela Lua e os satélites permanecem na órbita do nosso planeta e também por permanecermos em órbita ao redor do Sol.