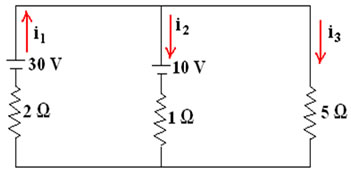
Às vezes nos deparamos com situações como a da figura acima, onde, no circuito, os resistores não estão ligados nem em série e nem em paralelo, ou seja, os circuitos são complexos. Para calcularmos o valor da corrente que percorre o circuito fazemos o uso de algumas regras denominadas Regras de Kirchhoff.
Regra dos nós
Em um nó, a soma das correntes que chegam com as correntes que saem é igual.
Obs.: Nós são pontos em um circuito onde as correntes elétricas são divididas ou são juntas. Na figura abaixo são considerados nós os pontos A e B, pois são os pontos onde a corrente se divide (A) e onde a corrente se junta (B).

Os pontos A e B são denominados de nós
Regra das Malhas
Damos o nome de malhas a um percurso fechado qualquer em um circuito. Nesse circuito, a soma algébrica das variações de potencial deve ser nula.

Malhas de um circuito
Utilizando a Regra de Kirchhoff:

Através da regra de Kirchhoff vamos calcular o valor da corrente elétrica do circuito. Para o circuito fechado adotaremos o sentido anti-horário.
Partindo do ponto A, ao passarmos por R1, estamos indo do potencial menor para o maior, portanto estamos ganhando potencial.
+R1 . i = +5i
Quando passamos por E2, estamos indo do potencial menor para o maior potencial, assim estamos ganhando potencial.
+60 V
Ao passarmos por R2, estamos indo do potencial menor para o maior e, assim, ganhamos potencial.
+R2 . i = +3i
Quando passamos por E1, vamos do potencial maior para o menor. Assim, perdemos potencial.
-100 V
Somando todas as variações do circuito fechado temos:
+5i + 60 + 3i – 100 = 0
8i = 40
i = 5 A
Então podemos concluir que a corrente que percorre o circuito é igual a 5 ampère.