A aceleração da gravidade é um dos responsáveis pelo movimento de queda livre dos objetos, sendo seu valor na superfície terrestre de aproximadamente \(9,8\ {m}/{s^2}\). Contudo, esse valor não é constante, já que ele varia com a latitude, altitude, geologia e outros fatores. Em razão disso, cada corpo celeste possui um valor diferente de aceleração da gravidade, como no caso do Sol, onde o valor é de aproximadamente \(274\ {m}/{s^2}\), enquanto na lua o valor é de aproximadamente \(1,62\ {m}/{s^2}\).
Saiba mais: Imponderabilidade — a sensação de ausência de peso provocada em um objeto que orbita a Terra
Tópicos deste artigo
- 1 - Resumo sobre aceleração da gravidade
- 2 - O que é a aceleração da gravidade?
- 3 - Qual o valor da aceleração da gravidade?
- 4 - Quais são as fórmulas da aceleração da gravidade?
- 5 - Como se calcula a aceleração da gravidade?
- 6 - Qual é a aceleração da gravidade em outros planetas?
- 7 - Exercícios resolvidos sobre aceleração da gravidade
Resumo sobre aceleração da gravidade
-
A aceleração da gravidade determina a aceleração sofrida por um corpo devido à força de atração que a Terra realiza sobre todos os corpos.
-
Se desconsiderarmos a resistência do ar, todos os corpos caem com a mesma aceleração.
-
Nos exercícios, por fins de facilidade, é comum calcular a aceleração da gravidade terrestre com valor de \(10\ {m}/{s^2}\).
-
Como a Terra possui formado geoide, com polos achatados, sua aceleração da gravidade sofre variações de valor, ainda que pequenos.
-
Quanto mais alto estivermos, menor será a aceleração da gravidade.
-
Quanto mais próximos estivermos dos polos da Terra, maior será a aceleração da gravidade.
-
Podemos calcular a aceleração da gravidade de duas formas distintas, uma para o caso de o objeto estar distante e outra caso o objeto esteja na superfície do corpo celeste.
O que é a aceleração da gravidade?
A aceleração da gravidade é uma grandeza física vetorial que determina a aceleração sofrida por um corpo devido à força de atração que a Terra realiza sobre todos os corpos, de acordo com a lei da gravitação universal de Isaac Newton (1642-1727).
Na Cinemática, no estudo da queda livre, tratamos a aceleração da gravidade como a aceleração vertical sofrida pelos corpos em queda. Seu valor é igual para todos que estão no mesmo corpo celeste (no nosso caso, na Terra). Assim, o tempo de queda dos objetos de uma mesma altura é o mesmo, independentemente da massa e desconsiderando a resistência do ar, que é uma força contrária ao movimento de queda.
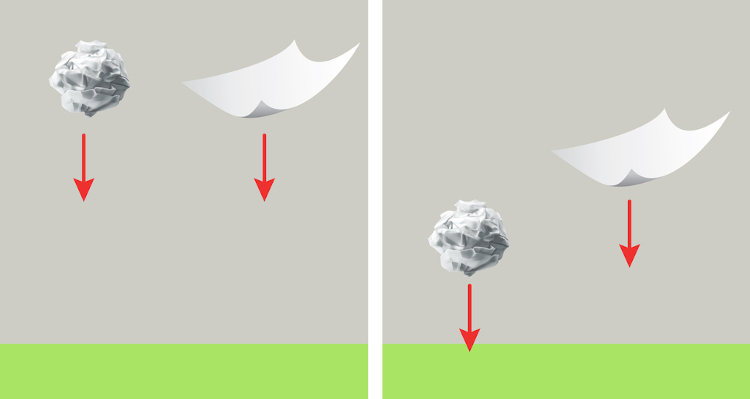
Contudo, na realidade, não podemos desconsiderar a resistência do ar, de modo que isso ocorre em exercícios com fins didáticos. Devido a essa resistência, objetos com maior massa ou menor superfície caem mais rápido do que objetos mais leves, como no caso de uma folha de papel amassada e uma aberta, conforme podemos ver na imagem abaixo.
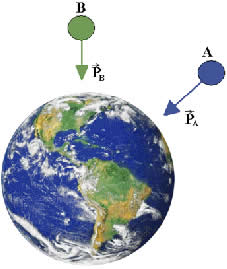
Por ser uma grandeza física vetorial, a aceleração da gravidade possui características específicas, sendo elas:
-
Módulo: cálculado pela fórmula da aceleração da gravidade.
-
Sentido: em direção ao centro da Terra, normalmente para baixo.
-
Direção: vertical.
Qual o valor da aceleração da gravidade?
A aceleração da gravidade na superfície terrestre é de aproximadamente 9,8 m/s2, contudo esse valor varia de acordo com alguns fatores como latitude, altitude, topografia, geologia e intensidade da força gravitacional. Isso acontece porque a Terra não é uma circunferência perfeita — ela possui um formato geoide, com os polos achatados, fazendo com que a aceleração da gravidade varie.

Sendo assim, o valor da aceleração da gravidade varia inversamente com a altitude. Quanto mais altos estivermos em relação ao nível do mar, menor será a gravidade. Na superfície do oceano Ártico, por exemplo, seu valor é de aproximadamente \(9,8337\ {m}/{s^2}\), enquanto na montanha de Huascarán, no Peru, fica em torno de \(9,7639\ {m}/{s^2}\).
Além disso, quanto mais nos afastamos da Linha do Equador (linha imaginária que corta o planeta ao meio horizontalmente), maior será a gravidade. Nessa linha, a gravidade gira em torno de \(9,789\ {m}/{s^2}\); nos polos terrestres, ela vale aproximadamente \(9,823\ {m}/{s^2}\).
Quais são as fórmulas da aceleração da gravidade?
→ Aceleração da gravidade na superfície do planeta ou corpo celeste
\(g=\frac{G\bullet m}{r^2}\)
-
g → aceleração da gravidade, medida em \([m/s^2]\).
-
G → constante de gravitação universal, igual a \(6,67\bullet{10}^{-11}\ N.m^2/{kg}^2\).
-
m → massa do planeta, medida em quilogramas [kg].
-
r → raio médio do corpo celeste, medido em metros [m].
→ Aceleração da gravidade para corpos externos ao planeta ou corpo celeste
\(g=\frac{G\bullet m}{({r+h)}^2}\)
-
g → aceleração da gravidade, medida em \([m/s^2]\).
-
G → constante de gravitação universal, igual a \(6,67\bullet{10}^{-11}\ N.m^2/{kg}^2\).
-
m → massa do planeta, medida em quilogramas [kg].
-
r → raio médio do corpo celeste, medido em metros [m].
-
h → altura entre o objeto e a superfície do planeta, medida em metros [m].
Saiba também: Velocidade de escape — a menor velocidade necessária para um corpo escapar da atração da gravidade
Como se calcula a aceleração da gravidade?
Podemos calcular a aceleração da gravidade por meio das fórmulas estudadas no tópico anterior, sendo que cada uma servirá para um caso específico — uma caso o objeto esteja na superfície planetária e outra caso o objeto esteja distante dela. Além disso, vale resaltar que caso nos exercícios não seja dado o valor da aceleração da gravidade terrestre, podemos considerá-la \(10\ {m}/{s^2}\).
-
Exemplo 1:
Determine o módulo da aceleração da gravidade da Terra, sabendo que seu raio médio é de 6.371 km e sua massa é de \(5,972\bullet{10}^{24}\ kg\).
Resolução:
Usando a fórmula da aceleração da gravidade na superfície do planeta:
\(g=\frac{G\bullet m}{r^2}\)
Vamos converter o valor do raio médio de quilômetros para metros (\(6.371\ km=6371000\ m=6,371\bullet{10}^6\)):
\(g=\frac{6,7\bullet{10}^{-11}\bullet5,972\bullet{10}^{24}}{{(6,371\bullet{10}^6)}^2}\)
\(g=\frac{40,0124\bullet{10}^{-11+24}}{40,589641\bullet{10}^{12}}\)
\(g=\frac{40,0124\bullet{10}^{13}}{40,589641\bullet{10}^{12}}\)
\(g=0,985778613\bullet{10}^{13-12}\)
\(g=0,985778613\bullet{10}^1\)
\(g=9,85778613\)
\(g\approx9,8{\ m}/{s^2}\)
A aceleração da gravidade na superfície da Terra tem valor de, aproximadamente, \(9,8{\ m}/{s^2}\).
-
Exemplo 2:
Determine o módulo da aceleração da gravidade da Terra para um objeto a 1000 km da superfície terrestre, sabendo que o raio médio do planeta é de 6.371 km e sua massa é de \(5,972\bullet{10}^{24}\ kg\).
Resolução:
Usando a fórmula da aceleração da gravidade para corpos externos ao planeta ou corpo celeste:
\(g=\frac{G\bullet m}{({r+h)}^2}\)
Vamos converter o valor do raio médio e a distância do objeto de quilômetros para metros (\(6.371\ km=6371000\ m=6,371\bullet{10}^6\) e \(1000\ km=1\bullet{10}^6\ m\), respectivamente):
\(g=\frac{6,7\bullet{10}^{-11}\bullet5,972\bullet{10}^{24}}{{(6,371\bullet{10}^6+1\bullet{10}^6)}^2}\)
\(g=\frac{40,0124\bullet{10}^{-11+24}}{{(7,371\bullet{10}^6)}^2}\)
\(g=\frac{40,0124\bullet{10}^{13}}{54,331641\bullet{10}^{12}}\)
\(g\approx0,7366\bullet{10}^{13-12}\)
\(g\approx0,7366\bullet{10}^1\)
\(g\approx7,366{\ m}/{s^2}\ \)
A aceleração da gravidade sentida no corpo que está externo ao planeta tem valor de, aproximadamente, \(7,366{\ m}/{s^2}\).
Qual é a aceleração da gravidade em outros planetas?
Como dito anteriormente, cada corpo celeste possui um valor de aceleração da gravidade. Esses valores estão descritos na tabela abaixo.
|
Corpo celeste |
Aceleração da gravidade \(({m}/{s^2})\) |
|
Sol |
274 |
|
3,7 |
|
|
8,87 |
|
|
Terra |
9,807 |
|
1,62 |
|
|
3,721 |
|
|
24,79 |
|
|
10,44 |
|
|
8,87 |
|
|
11,15 |
|
|
0,62 |
Exercícios resolvidos sobre aceleração da gravidade
Questão 1
Determine o módulo da aceleração da gravidade de Marte, sabendo que seu raio médio é de 3400 km (3,4·106 m) e que a sua massa é de 6,4·1023 kg.
Dados: G = 6,7·10-11 Nm²/kg²
A) 5,20 m/s²
B) 3,71 m/s²
C) 9,8 m/s²
D) 4,15 m/s²
E) 12,7 m/s²
Resolução:
Alternativa B
Para encontrarmos o valor da gravidade do planeta Marte, usamos a fórmula da aceleração da gravidade:
\(g=\frac{G\bullet M}{r^2}\)
\(g=\frac{6,7\bullet{10}^{-11}\bullet6,4\bullet{10}^{23}}{{(3,4\bullet{10}^6)}^2}\)
\(g=\frac{6,7\bullet{10}^{-11}\bullet6,4\bullet{10}^{23}}{11,56{\bullet10}^{12}}\)
\(g\approx3,71\bullet{10}^{-11+23-12}\)
\(g\approx3,71\bullet{10}^0\)
\(g\approx3,71\bullet1\)
\(g\approx3,71\ m/s^2\)
Questão 2
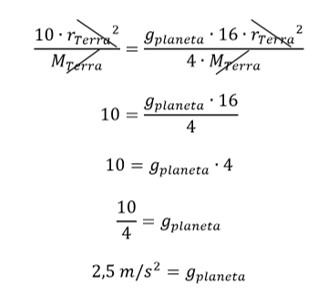
(UFGRS) Considerando que o módulo da aceleração da gravidade na Terra é igual a 10 m/s2, é correto afirmar que se existisse um planeta cuja massa e cujo raio fossem quatro vezes superiores aos da Terra, a aceleração da gravidade seria de:
A) 2,5 m/s2
B) 5 m/s2
C) 10 m/s2
D) 20 m/s2
E) 40 m/s2
Resolução:
Alternativa A
Isolando a constante gravitacional G da fórmula da aceleração gravitacional:
\(g=\frac{G\bullet M}{r^2}\)
\(G=\frac{g\bullet r^2}{M}\)
Igualando o valor das constantes gravitacionais da Terra e do planeta, faremos uma comparação entre eles: